 |
г) с увеличением значения признака “х” на единицу значение признака “у” увеличивается на 16.
|
|
|
|
Тест 5.
«Измерение связи».
1. Если значение коэффициента корреляции равно – 1, то:
а) связь полная прямая;
б) связь полная обратная;
в) связь отсутствует.
2. Выражение для определения коэффициента корреляции имеет вид:
а) 
,
б) 
,
в) 
,
г)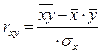 
,
3. Регрессия – это:
а) изменение результативного признака;
б) ошибка аппроксимации;
в) функция, которая отражает зависимость величины результативного признака от заданных фиксированных значений факторных признаков;
г) корреляционная связь.
4. Простейшим приемом выявления корреляционной связи между двумя признаками является:
а) расчет коэффициента корреляции знаков;
б) расчет коэффициента эластичности;
в) построение уравнения корреляционной связи;
г) анализ корреляционного поля.
5. Эмпирическое корреляционное отношение представляет собой корень квадратный из отношения:
а) средней из групповых дисперсий к общей дисперсии;
б) межгрупповой дисперсии к общей дисперсии;
в) межгрупповой дисперсии к средней из групповых дисперсий;
г) средней из групповых дисперсий к межгрупповой дисперсии.
6. Парный коэффициент корреляции показывает:
а) тесноту линейной зависимости между двумя признаками на фоне действия остальных, входящих в модель;
б) тесноту линейной зависимости между двумя признаками при исключении влияния остальных, входящих в модель;
в) тесноту нелинейной зависимости между двумя признаками;
г) тесноту связи между результативным признаком и остальными, включенными в модель.
7. Частный коэффициент корреляции показывает:
а) тесноту линейной зависимости между двумя признаками на фоне действия остальных, входящих в модель;
|
|
|
б) тесноту линейной зависимости между двумя признаками при исключении влияния остальных, входящих в модель;
в) тесноту нелинейной зависимости;
г) тесноту связи между результативным признаком и остальными, включенными в модель.
8. Парный коэффициент корреляции может принимать значения:
а) от 0 до 1;
б) от –1 до 0;
в) от –1 до 1;
г) любое значение меньше нуля.
9. Множественный коэффициент корреляции может принимать значения:
а) от 0 до 1;
б) от –1 до 0;
в) от –1 до 1;
г) любое значение меньше нуля.
10. Коэффициент детерминации может принимать значения:
а) от 0 до 1;
б) от –1 до 0;
в) от –1 до 1;
г) любое значение меньше нуля.
11. С помощью какого уравнения регрессии исследуется прямолинейная связь между факторами:
а)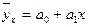 
;
б) 
;
в) 
;
г) 
.
12. Какие формулы используются для аналитического выражения нелинейной связи между факторами:
а) ;
б) .
в) верны оба варианта.
13. Для изучения связи между двумя признаками рассчитано линейное уравнение регрессии:
параметры: 
Параметр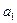 
показывает, что:
а) связь между признаками прямая;
б) связь между признаками обратная;
в) с увеличением значения признака “ х ” на единицу значение признака “ у ” увеличивается на 78;
г) с увеличением значения признака “х” на единицу значение признака “у” увеличивается на 16.
14. В результате проведения регрессионного анализа получают функцию, описывающую:
а) взаимосвязь показателей;
б) соотношение показателей;
в) структуру показателей;
г) темпы роста показателей;
15. Параболическое уравнение регрессии применяется, если:
а) при равномерном возрастании факторной переменной результативный признак возрастает или убывает ускоренно;
б) результативный и факторный признаки возрастают или убывают примерно одинаково (в арифметической прогрессии);
в) при увеличении значений факторной переменной значения результативного признака не изменяются.
|
|
|
16. Линейное уравнение регрессии применяется, если:
а) при равномерном возрастании факторной переменной результативный признак возрастает или убывает ускоренно;
б) результативный и факторный признаки возрастают или убывают примерно одинаково (в арифметической прогрессии);
в) при увеличении значений факторной переменной значения результативного признака не изменяются.
17. Гиперболическое уравнение регрессии применяется, если:
а) при равномерном возрастании факторной переменной результативный признак возрастает или убывает ускоренно;
б) при увеличении значений факторной переменной значения результативного признака уменьшаются, причем это уменьшение все время замедляется;
в) при увеличении значений факторной переменной значения результативного признака увеличиваются, причем это увеличение все время возрастает;
г) результативный и факторный признаки возрастают или убывают примерно одинаково (в арифметической прогрессии);
18. Для определения параметров уравнения регрессии можно применить метод:
а) скользящей средней;
б) наименьших квадратов;
в) основного массива;
г) параллельных рядов.
19. Если коэффициент детерминации равен 1, то:
а) отклонения эмпирических значений от теоретических отсутствуют;
б) все теоретические значения совпадают со средним значением;
в) связь функциональная;
г) связь отсутствует.
20. Если есть основания полагать, что при любых уровнях факторного признака Х увеличение его на единицу вызывает одинаковый прирост результативного признака У, то для измерения связи целесообразно использовать уравнение:
а) линейное;
б) экспоненты;
в) параболы второго порядка;
г) гиперболы.
21. Линейный коэффициент корреляции характеризует:
а) существенность и направление связи;
б) направление и тесноту связи;
в) тесноту связи;
г) направление связи.
22. По линейному уравнению регрессии вычислены показатели: линейный коэффициент корреляции = 0,7; индекс корреляции = 0,75; коэффициент детерминации = 0,49; коэффициент регрессии = 0,26. При вычислении какого показателя допущена ошибка:
а) линейного коэффициента корреляции;
|
|
|
б) индекса корреляции;
в) коэффициента детерминации;
г) коэффициента регрессии.
23. Линейный коэффициент корреляции между потреблением молока и числом детей в семье = 0,2. Это означает, что с вариацией факторного признака связано:
а) 4 % вариации результативного признака;
б) 96 % вариации результативного признака;
в) 80 % вариации результативного признака;
г) 20 % вариации результативного признака.
|
|
|
