 |
Третье начало термодинамики (теорема Нернста)
|
|
|
|
Третье начало термодинамики было установлено В. Нернстом в 1906 году на основании экспериментальных исследований свойств веществ при низких температурах. По историческим причинам этот закон получил название тепловой теоремы Нернста, хотя он не может быть выведен логическим путем из остальных начал термодинамики и является постулатом.
Третье начало термодинамики включает в себя два утверждения:
1) при приближении температуры к абсолютному нулю, энтропия системы стремится к конечному предельному значению S 0;
2) все процессы при абсолютном нуле температур, переводящие систему из одного равновесного состояния в другое, происходят без изменения энтропии.
Чтобы понять важность первого утверждения, вспомним, что изменение энтропии при обратимом переходе системы из состояния 1 в состояние 2 равно приведенному количеству теплоты. В частности, при изохорном процессе
. (18.1)
В подынтегральном выражении температура Т стоит в знаменателе. Поэтому не очевидно, будет интеграл сходиться или нет, если, например, Т 2 будет стремиться к нулю. Первая часть теоремы Нернста утверждает, что интеграл сходится.
Из второй части следует, что предел S 0, к которому стремится энтропия при Т ® 0, не меняется при изменении объема, давления и других параметров, а значит не зависит от состояния системы. Поэтому значение S 0 можно принимать одинаковым для всех систем. Удобнее всего условиться считать энтропию всякой равновесной системы при абсолютном нуле температуры равной нулю. Тогда третье начало термодинамики можно сформулировать следующим образом.
При приближении температуры к абсолютному нулю энтропия системы также стремится к нулю, независимо от того, какие значения принимают при этом остальные параметры состояния.
|
|
|
Второе начало термодинамики дает возможность находить изменение энтропии при переходе из одного состояния в другое. Энтропия при этом определяется с точностью до аддитивной постоянной.
Третье начало позволяет избавиться от неоднозначности в термодинамическом определении энтропии и связанных с ней термодинамических функций. Энтропию системы можно находить, зная зависимость теплоемкости от температуры.
. (18.2)
Интегралы в формулах (18.2) должны сходиться, следовательно СV ® 0 и СР ® 0 при Т ® 0.
Так как при Т = 0 энтропия перестает зависеть от давления и объема, при Т ® 0 ее производные
.
Тогда из соотношений Максвелла 
и 
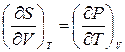следует, что при стремлении температуры к нулю, стремятся к нулю коэффициент объемного расширения 
и температурный коэффициент давления 
.
Из третьего начала термодинамики следует недостижимость абсолютного нуля температуры. Согласно этому закону нулевая изотерма Т = 0 совпадает с нулевой адиабатой S = 0. Охлаждение при приближении к абсолютному нулю осуществляется в результате адиабатических процессов, в которых система совершает работу за счет убыли внутренней энергии. Так как адиабаты S = const не пересекаются, то состояние с S = 0 не может быть достигнуто никаким адиабатическим процессом. Поэтому нельзя достигнуть и изотермы Т = 0, которая одновременно является адиабатой S = 0, к ней можно только асимптотически приближаться. По этой причине третьим началом термодинамики часто называют принцип недостижимости абсолютного нуля. Именно в такой форме его формулировал Нернст, который не любил понятие энтропии и не употреблял его.
Эффект Джоуля – Томсона
Эффектом Джоуля-Томсона называют изменение температуры при протекании газа под действием перепада давлений сквозь какое-либо локальное препятствие – дроссель. Дросселем может служить пористая перегородка, узкий участок трубки, вентиль и т.п. Система, в которой наблюдается процесс Джоуля-Томсона (процесс дросселирования), изображена на рис. 19.1.
|
|
|
В теплоизолированной трубке помещена пробка из пористого материала. Под действием разности давлений газ медленно протекает через перегородку. Благодаря медленности процесса в газе не возникает турбулентных течений. Кроме того, можно пренебрегать кинетической энергией упорядоченного движения. В таких условиях состояния газа по обе стороны перегородки можно считать равновесными. На начальных этапах процесса пробка и газ обменивались теплотой. С течением времени процесс становится стационарным, внутренняя энергия пробки перестает меняться. Слева от перегородки давление газа Р 1 и температура Т 1 поддерживаются постоянными. При стационарном течении по правую сторону перегородки устанавливается давление Р 2, которое всегда меньше Р 1, и температура Т 2. Если газ охлаждается (Т 2 < T 1) эффект Джоуля-Томсона называется положительным, а если нагревается (T 2 > T 1) – отрицательным.
Рассмотрим прохождение через перегородку некоторой порции газа. Пусть по левую сторону от дросселя она имела объем V 1и внутреннюю энергию U 1, а после прохождения имеет объем V 2 и внутреннюю энергию U 2. Полученное газом тепло равно нулю, так как в стационарных условиях теплообмен между газом и пробкой уже прекратился, а стенки трубки адиабатические. Тогда изменение внутренней энергии равно работе, произведенной над газом внешними силами.
.
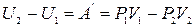Это соотношение можно переписать в виде
,
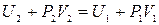или, вспомнив, что энтальпия H = U + PV,
Н 2 = Н 1.
Таким образом, в процессе Джоуля-Томсона энтальпия газа остается неизменной.
Так как энтальпия идеального газа зависит только от температуры, то из постоянства энтальпии следует, что температура идеального газа в процессе Джоуля-Томсона не меняется. Для реальных газов процесс сопровождается либо нагреванием, либо охлаждением. Поскольку при дросселировании всегда 
, знак эффекта определяется знаком отношения 
. Если рассматривать дифференциальный эффект Джоуля-Томсона, когда перепад давлений мал (
), можно считать
.
Чтобы найти производную (¶ T/ ¶ P) H запишем дифференциал энтальпии в переменных температура и объем Н = Н (Т,Р) и приравняем его нулю
|
|
|
.
Из этого следует
. (19.1)
Так как 
, то 
.
Используя соотношение Максвелла (16.8), получим
. (19.2)
Учитывая, что 
, можно записать
. (19.3)
Теплоемкость СР всегда больше нуля, поэтому знак эффекта Джоуля-Томсона определяется знаком числителя правой части равенства (19.3). Чтобы его определить, достаточно знать уравнение состояния газа. Если газ идеальный, то 
, а потому D Т = 0. Изменение температуры реальных газов будет рассмотрено позднее, когда в нашем распоряжении будут уравнения состояния реальных газов.
Наряду с дифференциальным эффектом рассматривают также интегральный эффект Джоуля-Томсона. В этом случае перепад давлений велик, и может составлять десятки и даже сотни атмосфер. Изменения температуры тоже значительны. Поэтому интегральный эффект применяется для получения низких температур. При вычислении изменения температуры можно рассматривать интегральный эффект как последовательность дифференциальных эффектов. Таким путем приходим к выражению
. (19.4)
При практическом использовании эффекта Джоуля-Томсона часто бывает, что в исходном состоянии газ находится под высоким давлением, а после дросселирования давление падает настолько низко, что газ можно считать идеальным. В этом случае изменение температуры проще найти не по формуле (19.4), а непосредственно пользуясь равенством энтальпий в начальном и конечном состояниях. Соответствующий расчет будет проведен позднее для газа Ван-дер-Ваальса.
|
|
|
