Катушки индуктивности и взаимной индуктивности.

Элементы электрических измерительных цепей

Основными составляющими электрических измерительных приборов являются резисторы для цепей переменного тока, измерительные конденсаторы, измерительные катушки индуктивности и взаимной индуктивности.

Измерительный резистор. В идеальном резисторе вектор тока совпадает по направлению с вектором напряжения. В реальном резисторе всегда присутствует межвитковая емкость и индуктивность, так как проволочный резистор является катушкой, а изоляция витков является обкладками конденсатора. Современные резисторы, основанные на применении керамических материалов, обеспечивают величину сопротивления за счет присутствия проводящих примесей. Они боле миниатюрны и лишены таких явлений, как паразитная емкость и индуктивность.

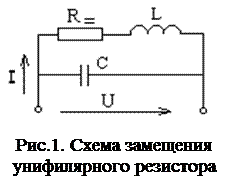Рассмотрим эквивалентную схему замещения резистора с унифилярной обмоткой для цепи переменного тока.

Она включает в себя L – индуктивность обмотки, С – емкость, включенная между концами резистора, R₌ - сопротивление резистора для цепи постоянного тока.

Полное сопротивление резистора имеет вид

(1.1)

Для частот до 200 кГц можно приравнять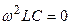

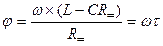, (1.2)

где - постоянная времени, с;

щ - частота сети, Гц.

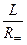= = - СR₌. (1.3)

Для частот выше 200 кГц полное сопротивление составит

z = . (1.4)

Активное сопротивление

r = . (1.5)

Если за полное сопротивление резистора на переменном токе принимается R₌, определенное на постоянном токе, то вносится поправка

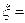
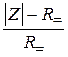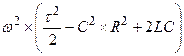= . (1.6)

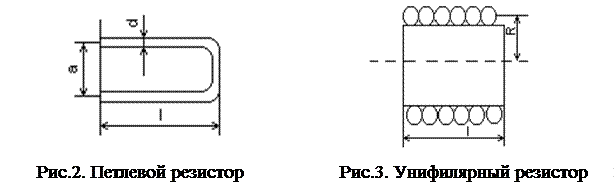При изготовлении резисторов для исключения влияния реактивного сопротивления производят намотку петлевым или унифилярным способом.

Петлевой резистор L Гн. (рис.2)

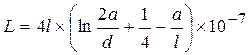. (1.7)

Резистор с унифилярной обмоткой (рис.3)

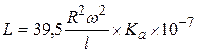(1.8)

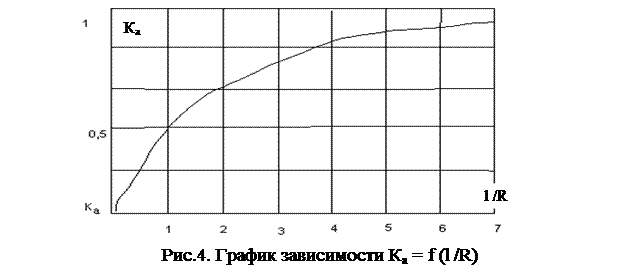
Все размеры выражаются в метрах, а коэффициент К_а определяется в соответствии с кривой, представленной на рисунке 4.

Измерительные конденсаторы. Предназначены для работы при низких напряжениях, имеют плоскую форму, а для работы при высоких напряжениях цилиндрическую (коаксиально расположенные проводящие цилиндры).

Емкость С [Ф] для плоского конденсатора

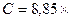
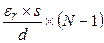, (1.9)

где s – площадь обкладки, м²;

d – расстояние между обкладками, мм;

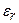- относительная диэлектрическая проницаемость диэлектрика.

Емкость цилиндрического конденсатора

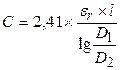, (1.10)

где l – длина цилиндра, м;

D₁ – внешний диаметр внутреннего цилиндра, м;

D₂ - внутренний диаметр внешнего цилиндра, м.

Катушки индуктивности и взаимной индуктивности.

Катушка с каркасом прямоугольного сечения (рис. 5.а)

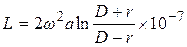. (1.11)

Катушка с каркасом круглого сечения (рис.5.б)

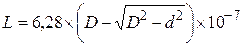. (1.12)

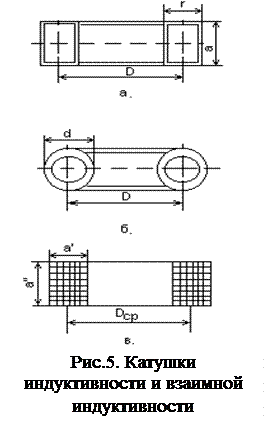Взаимная индуктивность тороидальной катушки прямоугольного сечения

М = 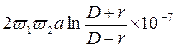. (1.13)

Взаимная индуктивность тороидальной катушки круглого сечения

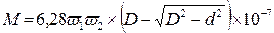, (1.14)

где 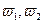- число витков катушки;

D – средний диаметр катушек;

а, r – аксиальный и радиальный размеры средних витков катушек;

d – диаметр среднего витка внутренней катушки.

Расчет производится с помощью комплексного магнитного сопротивления

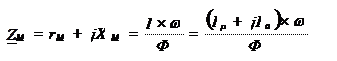, (1.15)

или

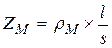= , (1.16)

где 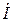- ток в катушке, А;

I 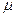- намагничивающая составляющая ток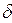а , А;

I_а –составляющая тока 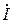обусловленная потерями в магнитопроводе, А;

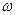- число витков;

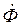- магнитный поток, Вб;

_М – удельное магнитное сопротивление материала, (АЧм)/Вб;

l, s – средняя длинна и сечение магнитопровода, м;

r_мо - удельное активное сопротивление материала магнитопровода, Ам/Вб;

Х_мо – удельное реактивное сопротивление материала магнитопровода, Ам/Вб.

Полное сопротивление катушки индуктивности с магнитопроводом

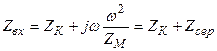= r_эф + 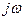L_эф, (1.17)

где Z_К – комплексное сопротивление обмотки, Ом;

Z_сер = 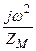- сопротивление вносимое магнитопроводом, Ом.

Активное сопротивление магнитопровода

r_эф = r_к + 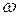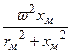. (1.18)

Реактивное сопротивление магнитопровода

L_эф = L_S + 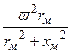. (1.19)

Комплексное магнитное сопротивление магнитопровода, имеющего воздушный зазор

Z_М = r_мв + Z_МС = 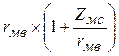, (1.20)

где Z_МС – комплексное магнитное сопротивление магнитопровода;

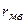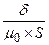= - магнитное сопротивление воздушного зазора, Ом;

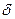- длинна воздушного зазора, м;

S – средняя площадь сечения магнитного потока в воздушном зазоре, равная площади сердечника, м;

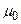- магнитная постоянная - 4 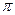10^-7 Г/м.

Полное сопротивление катушки индуктивности, имеющей воздушный зазор при условии 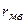>> Z_МС

Z_М = Z_К + 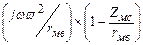. (1.21)

Взаимная индуктивность между обмотками катушки с магнитопроводом

М = 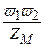. (1.22)

Добротность катушки

Q = 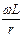. (1.23)

ПРИМЕР РЕШЕНИЯ ЗАДАЧ

Задача

При синусоидальном токе I₁ = 50 мА в первичной обмотке катушки взаимной индуктивности с магнитопроводом, напряжение на разомкнутых зажимах вторичной обмотки равно Е = 3 В и отстает от I₁ на угол 120⁰. Определите комплексное магнитное сопротивление, удельное комплексное магнитное сопротивление материала магнитопровода, если f = 50 Гц, 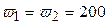, площадь поперечного сечения S = 4 см², средняя длинна силовой линии l_ср = 20 см.

Решение

Считаем, что ток I₁ совпадает с осью вещественных величин. Определим значения для комплекса ЭДС и Ф - магнитного потока

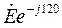. (1.24)

. (1.25)

Комплексное магнитное сопротивление магнитопровода

Z_М = 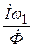= 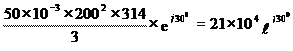А/Вб

Удельное комплексное магнитное сопротивление материала магнитопровода

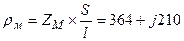(АЧм)/Вб

 

12	Поделиться:

Воспользуйтесь поиском по сайту: