Передача тепла через плоскую многослойную стенку при граничных условиях 3-ого рода

Передача тепла через плоскую стенку

Передача тепла через плоскую однослойную стенку при граничных условиях 1-ого рода

Расчётная схема имеет вид, представленный на рис. 1. Исходные данные – температуры на поверхностях стенки t₁ и t₂ (t₁>t₂), толщина стенки δ (м), коэффициент теплопроводности материала стенки λ (Вт/(м·К)).

Определить – плотность теплового потока через стенку q (Вт/м²), закон изменения температуры внутри стенки t(х).

Закон изменения температуры внутри стенки t(х) температурного поля находится на основе решения стационарного уравнения теплопроводности (уравнения Лапласа) для одномерного случая . В результате зависимость t(х) имеет вид

Рис. 1

Выражение для плотности теплового потока q выводится на основе уравнения Фурье и имеет вид

.

Передача тепла через плоскую однослойную стенку при граничных условиях 3–ого рода

Расчётная схема имеет вид, представленный на рис. 2. Исходные данные – температуры омывающих стенку жидкостей t_ж1 и t_ж2 (t_ж1>t_ж2), толщина стенки δ (м), коэффициент теплопроводности материала стенки λ (Вт/(м·К)), коэффициенты теплоотдачи α₁ и α₂ (Вт/(м²·К)), характеризующие интенсивность процессов передачи тепла через тепловые пограничные слои в первой и второй жидкостях.

Определить – плотность теплового потока q, температуры на поверхностях стенки t_c1 и t_c2.

Плотность теплового потока определяется на основе решения системы уравнений, состоящей из уравнения Ньютона - Рихмана, определяющего плотность теплового потока через тепловой пограничный слой, а также из уравнения для плотности теплового потока, передаваемого теплопроводностью через стенку. В итоге выражение для q имеет вид

,

Рис. 2

Величина

,

называется термическим сопротивлением теплопередачи (м²·К/Вт) и может быть представлена в виде

,

где -термическое сопротивление теплоотдачи со стороны 1-ой жидкости;

-термическое сопротивление теплоотдачи со стороны 2-ой жидкости;

– термическое сопротивление теплопроводности стенки.

Величина, обратная термическому сопротивлению теплопередачи

,

называется коэффициентом теплопередачи.

Температура стенки со стороны 1 – ой жидкости определяется выражением

.

Температура стенки со стороны 2 – ой жидкости определяется выражением

.

 

Передача тепла через плоскую многослойную стенку при граничных условиях 1-ого рода

Расчётная схема имеет вид, представленный на рис. 3. Исходные данные – плоская стенка, содержащая n слоёв с толщинами δ₁, δ₂,... δ_n (в случае, изображённом на рис. 3 n=3), выполненные из различных материалов с коэффициентами теплопроводности λ₁, λ₂,... λ_n; температуры на поверхностях стенки t₁ и t_n+1 (t₁>t_n+1).

Определить – плотность теплового потока через стенку q (Вт/м²), температуры на поверхностях контактов слоёв t₂, t₃,.. t_n.

Плотность теплового потока определяется по выражению

 

.

 

 

Рис. 3

Температура на поверхности контакта между к и к+1 слоями определяется выражением

.

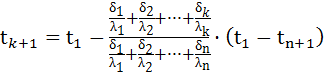Последнее выражение можно также представить в виде

,

где - термическое сопротивление теплопроводности первых k слоёв стенки;

где - термическое сопротивление теплопроводности всей стенки.

 

Передача тепла через плоскую многослойную стенку при граничных условиях 3-ого рода

Расчётная схема имеет вид, представленный на рис. 4. Исходные данные – плоская стенка, содержащая n слоёв с толщинами δ₁, δ₂,... δ_n (в случае, изображённом на рис. 4 n=2), выполненные из различных материалов с коэффициентами теплопроводности λ₁, λ₂,... λ_n; температуры жидкостей, омывающих стенку t_ж1 и t_ж2 (t_ж1>t_ж2), коэффициенты теплоотдачи α₁ и α₂

Определить – плотность теплового потока q, температуры на поверхностях стенки t₁ и t_n+1, а также температуры на поверхностях контактов слоёв t₂, t₃,.. t_n.

Плотность теплового потока определяется по выражению

 

.

 

 

Рис. 4

Температура стенки со стороны 1 – ой жидкости определяется выражением

.

Температура стенки со стороны 2 – ой жидкости определяется выражением

.

Температура на поверхности контакта между к и к+1 слоями определяется выражением

.

Последнее выражение можно также представить в виде

,

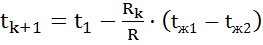где - термическое сопротивление теплопроводности первых k слоёв стенки и теплоотдачи со стороны первой жидкости;

где - термическое сопротивление теплопередачи через стенку.

Величина, обратная термическому сопротивлению теплопередачи

,

называется коэффициентом теплопередачи.

С учётом этого выражение для плотности теплового потока можно записать в виде

.

 

 

Поделиться:

Воспользуйтесь поиском по сайту: