Проверка теоремы Штейнера методом крутильных колебаний.

Лабораторная работа № 6

Определение момента инерции и проверка теоремы Штейнера методом крутильных колебаний.

Цель работы: изучить один из экспериментальных методов определения моментов инерции тел.

Приборы и принадлежности: трифилярный подвес, секундомер, штангенциркуль; набор тел подлежащих измерению.

Момент инерции I твердого тела относительно некоторой оси определяется выражением

,

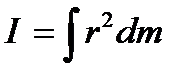где r - расстояние элемента массы dm от оси вращения.

В простых случаях величину момента инерции можно определять расчетом, а в сложных - его приходится находить экспериментальным путем. Одним из удобных методов измерения моментов инерции твердых тел является метод трифилярного подвеса.

Теория трифилярного подвеса

Схема трифилярного подвеса приведена на Рис 6.

Подвижная платформа Р' подвешена к платформе Р на трех симметрично расположенных нитях АА', ВВ'., СC'. -Платформа Р позволяет возбудить в. системе крутильные колебания. Вращательный импульс, необходимый для начала крутильных колебаний, сообщается платформе путем специального приспособления, которое находится сверху прибора, приводящего в движение рычажок, связанный с диском. Этим достигается почти полное отсутствие других крутильных колебаний, наличие которых затрудняет измерения. Для удобства отсчета колебаний на платформе имеется метка, против которой при покоящейся платформе устанавливается указатель - проволока на штативе.

При повороте нижней платформы Р' (относительно верхней) вокруг вертикальной оси на некоторый угол j возникает момент сил, стремящийся вернуть платформу в положение равновесия. Если пренебречь трением, то на основании закона сохранения энергии для колеблющейся системы можно записать: , (1)

где - кинетическая энергия системы, - потенциальная энергия системы, I - момент инерции платформы вместе с исследуемым телом, М - масса платформы с телом, z₀ -начальная координата

Рис. 6.

точки О' (при (j=0), z - координата точки О при текущем значении j. Точкой обозначено дифференцирование по времени.

Как следует из рис. 1., координаты точки С в системе координат (x,y,z) равны (r,0,0), а точка С' имеет координаты (Rcosj₀,Rsinj₀, Z), где j₀-максимальный угол отклонения. Расстояние между точками С и С’ равно длине нити l, Записывая l через значение ее координат (l²=x²+y²+z², где x²=(Rcosj₀-r)², y²=(Rsinj₀)², z²=z²), получим:

(R cosj₀ - r)²+ (R sinj₀)²+ z²=l²

z²=l²-R²-r²+2Rrcosj₀=Z₀²-2Rr(1-cosj₀),

так как Z²=l²-(R-r)²= l²-R²+2Rr-r².

Учитывая, что для малых углов отклонения j₀ cosj₀ » 1-j₀²/2, получим

Z²=Z₀²-Rrj₀ (2)

Приравнивая корень из выражения (2), найдем, что при малых углах j

(3)

Из (3) следует, что , (4).

т.к. Z₀=l. Считая, что платформа совершает гармонические колебания, можем записать зависимость углового смещения в виде:

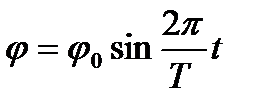, (5)

где j₀ - амплитуда отклонения, Т - период колебания, t - текущее время. Угловая скорость, являющаяся первой производной по времени, выражается так: 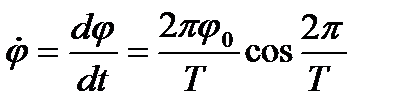(6)

В момент прохождения через положение равновесия

t=0, T/2,T,3T/2, ….(т.к. cos(2p/T) = ±1),

абсолютное значение этой величины будет

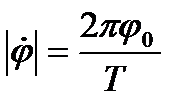, (7)

На основании вышеизложенного (выражений (1) и (7)) имеем

(8)

Подставляя в (8) выражение (4), получим

откуда (9)

По формуле (9) может быть определен момент инерции платформы и тела, положенного на нее, т.к. все величины в правой части формулы могут быть непосредственно измерены. Формула (9) справедлива при отсутствии в

системе потерь энергии на трение, или при t>>T, где Т - период колебаний системы, а t - время, в течение которого амплитуда колебаний платформы заметно уменьшается (в 2-3 раза).

Параметры трифилярного подвеса.

r = 0,06 м; l = 0,61 м;

R = 0,12 м; m₀ = (0,481+0,01) кг - масса пустой платформы.

 

Проверка теоремы Штейнера методом крутильных колебаний.

Для однородных и симметричных тел справедлива теорема Штейнера, которая формулируется следующим образом:

момент инерции I относительно произвольной оси равен сумме момента инерции I₀^’ относительно оси, параллельной данной и проходящей через центр инерции тела, и произведения массы тела m на квадрат расстояния d между осями:

I=I₀^’+md² (10)

Справедливость теоремы Штейнера можно проверить при помощи трифилярного подвеса, для чего необходимо иметь два совершенно одинаковых тела. Оба тела располагают симметрично на платформе и определяют их момент инерции при таком расположении. Половина этой величины и будет давать момент инерции одного тела, находящегося на фиксированном расстоянии от оси вращения. Зная это расстояние, массу тела и момент инерции тела, положенного в центре платформы, можно проверить теорему Штейнера

I=(I₂-I₀)/2=I₀^’+md², (11)

где I₂ - момент инерции двух грузов с платформой; I₀ - момент инерции пустой платформы; I₀^’ - момент инерции первого груза без платформы;

I - момент инерции первого груза без платформы, расположенного на расстоянии d от оси вращения.

Тела на платформе необходимо класть строго симметрично так, чтобы не было перекоса платформы, для чего на платформе нанесены цилиндрические окружности на определенном расстоянии друг от друга.

Измерения.

Сначала определяют по формуле (9) момент инерции пустой платформы I₀ ,. Так как величины l, R, r и масса платформы m₀ даются как постоянные прибора, то определяют только время периода колебаний пустой платформы Т₀. Для этого сообщают платформе вращательный импульс и при помощи секундомера измеряют время 50-ти полных колебаний, что дает возможность достаточно точно определить величину периода Т₀, После этого нагружают платформу в центре исследуемым телом, масса которого должна быть предварительно определена путем взвешивания, и вновь определяют период колебаний Т всей системы. Затем, пользуясь формулой..(9), вычисляют момент инерции I₁ всей системы, принимая ее массу m, равной сумме масс тела и платформы. Величина момента инерции тела I₀^’ определяется как разность I₀^’=I₁-I₀.

Далее нагружают платформу двумя одинаковыми телами, расположенными симметрично, и по формуле (9) определяют их момент инерции вместе с платформой I₂. Остальные результаты находят, благодаря соответствующим вычислениям.

При измерениях недопустимо пользоваться амплитудами колебаний, большими 5-6 градусов. Все данные измерений и расчетов свести в таблицу, проверить соотношение (2).

В работе использовать систему единиц СИ.

 

 

Таблица 1.

 

№	t0, сек (50 колебаний платформы)	T0 сек.	I0 кг*м2	t0, сек (50 колебаний с грузом 200 гр. в центре платформы)	T1 сек.	I0 кг*м2	t0, сек (50 колебаний с грузом 400 гр. по краям платформы)	T2 сек.	I0 кг*м2
	t0			t1			t2

 

Период ,. где N = 50.

Контрольные вопросы.

1. Что называется моментом инерции тела? В каких единицах измеряется момент инерции тела?

2. Выведите рабочую формулу. Какие упрощающие предположения следует использовать при выводе?

3. Справедлив ли указанный метод при определении момента инерции, если его центр инерции не лежит на оси вращения системы?

4. Сформулируйте и докажите теорему Штейнера.

Литература.

1. Савельев И.В. Курс общей физики. Т.Г. Наука. 1977.§§ 36-39.

2. Сивухин Д.В. Общий курс физики. Т.I. Наука. 1974. §§ 52,55-59.

 

 

Порядок выполнения работы:

1. Измерить время 50 колебаний для пустой платформы и для двух разных положений грузов на платформе. Каждый опыт повторяем 3 раза, затем считаем среднее значение времени. Значения величин перевести в СИ.

2. Вычислить периоды колебаний (3раза). Т = t /N

3. Вычислить моменты инерции (3 раза).

Параметры трифилярного подвеса.

r = 0,06 м; l = 0,61 м;

R = 0,12 м; m₀ = (0,481+0,01) кг - масса пустой платформы

М – масса груза (200 г или 400 г)

4. Проверить теорему Штейнера, подставив экспериментальные значения (I₂-I₀)/2=I₀^’+md²,

где I₂ - момент инерции двух грузов с платформой; I₀ - момент инерции пустой платформы; I₀^’ - момент инерции первого груза без платформы, определяется как разность I₀^’=I₁-I₀;

d - расстояние от оси вращения.

5. Вычислить прямую погрешность для 1 случая:

Δd (систематическая)и Δt (систематическая и случайная).

6. Записать конечный результат.

7. Сделать вывод.

 

Поделиться:

Воспользуйтесь поиском по сайту: