 |
Метод Гомори решения задач целочисленного программирования. Примеры решения экономических задач.
|
|
|
|
Графический метод решения задач целочисленного программирования.
При наличии в задаче линейного программирования двух переменных, а в системе ограничения – неравенств, она может быть решена графическим методом без требований целочисленных переменных.
Если оптимальное решение этой задачи является целочисленным, то оно и является оптимальным для исходной задачи.
Если же полученное оптимальное решение не целочисленное, то строится дополнительное линейное ограничение. Оно обладает следующими свойствами:
1. Оно должно быть линейным;
2. Должно отсекать найденный оптимальный не целочисленный план;
3. Не должно отсекать ни одного целочисленного плана.
Алгоритм графического решения задачи
Целочисленного программирования.
1. Построить систему координат x10х2и выбрать масштаб.
2. Найти область допустимых решений (ОДР) системы ограничений задачи.
3. Построить целевую функцию, являющуюся линией уровня и на ней указать направление нормали.
4. Переместить линию целевой функции по направлению нормали через ОДР, чтобы она из секущей стала касательной к ОДР и проходила через наиболее удаленную от начала координат точку. Эта точка будет являться точкой экстремума, т.е. решением задачи.
Если окажется, что линия целевой функции параллельна одной из сторон ОДР, то в этом случае экстремум достигается во всех точках соответствующей стороны, а задача линейного программирования будет иметь бесчисленное множество решений.
5. Найти координаты, точки экстремума и значение целевой функции в ней. Если полученные значения не целочисленные, то перейти к следующему шагу.
6. Выделить у этих координат область с целочисленными значениями.
|
|
|
7. Определить новые координаты и построить граф.
8. Найти точки с целыми значениями искомых переменных, подставить в уравнение целевой функции и найти её значение. Максимальное из полученных значений целевой функции и будет решением задачи.
Метод Гомори решения задач целочисленного программирования. Примеры решения экономических задач.
Данный метод основан на симплексном методе.
На первом этапе данная задача решается симплекс-методом, если полученное решение не целочисленное, то вводим дополнительное ограничение, которые должны быть:
- линейным;
- отсекать найденный оптимальный не целочисленный план;
- не должно отсекать ни одного целочисленного плана.
Дополнительное ограничение обладающие этими свойствами называются правильным отсечением.
Ограничение накладывается на нецелочисленную переменную или на ту переменную, которая имеет большее дробное значение. Ограничение накладывается на не целочисленную переменную через не основные переменные. Ограничение составляется используя следующее правило: дробная часть свободного члена берётся с тем же знаком, который он имеет и в уравнении, а дробные части неосновных переменных - с противоположным знаком и выделяется положительная дробь. Например, {a}=a, {-a}={-A+a*}, где А - целая часть отрицательное число, а*-положительная дробь.
Получаем новое ограничение, вводим новую основную переменную, приведённое в формуле (1.2.3).
где xn+1 - нововведённая переменная,
xj - переменные не входящие в базис.
Новое ограничение следует вводить в последний этап симплекс метода, когда все переменные, имеющиеся в целевой функции, так же входят в базис.
Полученное базисное решение всегда не допустимое, соответствующее правильному отсечению.
Для получения допустимого базисного решения необходимо перевести в основные переменную, входящую с положительным коэффициентом в уравнение, в котором свободный член отрицательный.
|
|
|
При выборе какую переменные ввести в базис взамен нововведённой, следует выразить эти переменные и следую логическому рассуждения, подставить в базис ту переменную которая даёт целочисленное решение на наложенное ограничение.
Введение новых ограничений следует производить, если не получено целочисленное решение, после решения на первом этапе симплекс-методом и после введения новых ограничений.
Если в процессе решения появится выражение с нецелым свободным членом и целыми остальными коэффициентами, то соответствующее уравнение не имеет решения в целых числах. В этом случае и данная задача не имеет целочисленного оптимального решения.
Задача. Контейнер объемом 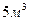 помещен на контейнеровоз грузоподъемностью 12т. Контейнер требуется заполнить грузом двух наименований. Масса единицы груза, объем единицы груза, стоимости приведены в таблице:
помещен на контейнеровоз грузоподъемностью 12т. Контейнер требуется заполнить грузом двух наименований. Масса единицы груза, объем единицы груза, стоимости приведены в таблице:
| Вид груза | 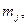 т т
| 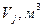
|  ден.ед. ден.ед.
|
Требуется загрузить контейнеровоз таким образом, чтобы стоимость перевозимого груза была максимальной.
Решим задачу методом Гомори.
Введем обозначения: х 1 – количество груза первого вида, х 2 – количество груза второго вида. Тогда экономико-математическая модель задачи примет вид:
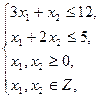
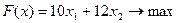 .
.
Преобразуем математическую модель ЗЛП без учета целочисленности переменных к допустимому предпочтительному виду канонической формы:

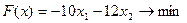 .
. 
По алгоритму основного симплекс-метода заполним симплексную таблицу решения ЗЛП:
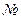
| 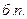
| 
| 
| 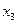
| 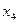
| 
|
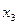
| ||||||
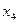 * *
| ||||||

| -10 | -12* | ||||
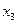 * *
| 5/2 | -1/2 | 19/2 | |||

| 1/2 | 1/2 | 5/2 | |||

| -4* | -30 | ||||
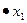
| 2/5 | -1/5 | 19/5 | |||

| -1/5 | 3/5 | 3/5 | |||

| 8/5 | 26/5 | -226/5 |
Оптимальное решение ЗЛП не удовлетворяет ограничению целочисленности, следовательно, к основным ограничениям необходимо добавить новое линейное ограничение.
Замечание 9.1. Если имеется несколько дробных 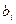 , то для той у которой дробная часть больше всего составляется ограничение.
, то для той у которой дробная часть больше всего составляется ограничение.
Составим сечение Гомори для первого ограничения оптимальной симплекс-таблицы решения ЗЛП (так как 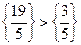 ):
):
|
|
|
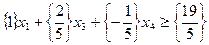 ,
,
иначе
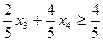 .
.
Преобразуем полученное ограничение к канонической форме с предпочтительной переменной:
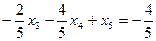 .
.
Продолжим решение задачи двойственным симплекс-методом, включив новое ограничение в оптимальную симплекс-таблицу решения ЗЛП:

| 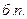
| 
| 
| 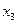
| 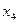
| 
| 
|

| 2/5 | -1/5 | 19/5 | ||||

| -1/5 | 3/5 | 3/5 | ||||
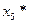
| -2/5 | -4/5 | -4/5 | ||||

| 8/5* | 26/5 | -226/5 | ||||

| |||||||

| |||||||
 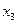
| -5/2 | ||||||

| -42 |
Оптимальное решение расширенной ЗЛП удовлетворяет ограничению целочисленности.
Ответ:  ,
, 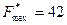 .
.
Таким образом, контейнер надо загрузить 3 ед. груза первого вида и 1 ед. второго вида, при этом стоимость перевозимого груза максимальна и равна 42 ден. ед.
Замечание 9.2. Если в процессе решения получена оптимальная таблица, в которой вспомогательная переменная имеет положительное значение, то соответствующая строка может быть вычеркнута.
|
|
|


