Дисперсия волн. Нормальная и аномальная дисперсия. Классическая теория дисперсии

ВЗАИМОДЕЙСТВИЕ СВЕТА С ВЕЩЕСТВОМ

Дисперсия света – это явления, обусловленные зависимостью показателя преломления вещества от длины волны (или частоты):

,

где λ – длина света в вакууме.

Производную называют дисперсией вещества.

При прохождение света через стеклянную призму на экране, установленном позади призмы, наблюдается радужная полоска (рис.3.5.1). Она называется призматическим или дисперсионным спектром. Образование призматического спектра является доказательством того, что абсолютный показатель преломления среды n зависит от частоты: n=n(n).

Для прозрачных бесцветных веществ график зависимости представлен на рис.3.5.2. Зависимости n от l нелинейные (рис.3.5.2), т.е. . Интервал длин волн, в котором , называется нормальной дисперсией (как на рис.3.5.2), а интервалы длин волн, где 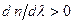, аномальной дисперсией (интервал l ₁ - l ₂ на рис.3.5.2). Область аномальной дисперсии совпадает с полосой поглощения .

Все вещества в той или иной степени являются диспергирующими. Вакуум дисперсией не обладает.

Аналитический вид зависимости n от l в области нормальной дисперсии может быть представлен приближенной формулой

где а и b – положительные постоянные, значения которых определяются экспериментально для каждого вещества.

Дисперсию света можно объяснить на основе электромагнитной теории вещества. В однородной изотропной среде . Диэлектрическая проницаемость среды , где – диэлектрическая восприимчивость. Вектор поляризации (дипольный момент единицы объема) 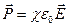, тогда

(3.5.1)

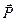где - проекция вектора на ось Х, вдоль которой совершаются колебания вектора 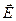. Очевидно, , где - концентрация диполей, - проекция дипольного момента отдельного диполя.

Будем рассматривать простейшую модель вещества, состоящую из невзаимодействующих друг с другом атомов. Каждый атом представляет собой ядро, окруженное быстро движущимися электронами, которые в совокупности как бы размазаны по сферической симметричной области вокруг ядра, т.е. ядро с зарядом q окружено электронным облаком с зарядом – q.

В отсутствие внешнего поля центр электронного облака совпадает с ядром, и дипольный момент атома равен нулю. При наличии внешнего поля электронное облако смещается относительно практически неподвижного ядра, и возникает дипольный момент , где - вектор, проведенный из центра облака к ядру. Проекция вектора на ось Х равна

где х – смещение центра облака из положения равновесия, т.е. относительно центра ядра. Тогда (3.5.1) можно переписать в виде:

(3.5.2)

Найдем под действием поля . Запишем уравнение движения электронного облака:

(3.5.3)

где т – масса электронного облака. Справа записаны проекции на ось Х квазиупругой силы, силы «сопротивления» (трения облака о ядро) и вынуждающей силы со стороны гармонической электромагнитной волны частоты ω. Разделив уравнение (3.5.2) на массу, имеем:

(3.5.4)

где .

Для теории дисперсии имеет значение не общее, а только частное (установившееся) решение уравнения (3.5.4):

,

где а – амплитуда колебаний, φ – разность фаз между смещением х и «силой» . Подставив это решение в уравнение (3.5.4), можно с помощью векторной диаграммы найти значения амплитуды и разности фаз:

Рассмотрим простейший случай, когда , т.е. частота вынуждающего поля далека от собственной частоты колебаний электронного облака, и затухание мало. В этом случае при имеем:

Подставив это выражение в (3.5.2), имеем:

(3.5.5)

где - концентрация электронов.

Разрыв функции при и обращение ее в не имеет физического смысла, это получается за счет игнорирования затухания.

Собственных частот может быть несколько в атоме. Столько же будет и областей аномальной дисперсии. Из рис.3.5.3 видно, что при показатель преломления будет меньше единицы. В этом случае фазовая скорость электромагнитной волны окажется больше скорости света. Подобное имеет место в плазме, где (электроны свободные), и для рентгеновского излучения (). Никакого противоречия с теорией относительности здесь нет. Последняя утверждает, что скорость сигнала (импульса) не может превышать скорость света с. Понятие же показателя преломления применимо к монохроматическим электромагнитным волнам, бесконечным в пространстве и во времени. Такие волны не могут служить для передачи сигнала, а кроме того, их в принципе невозможно осуществить.

Из выражения (3.5.5) следует, что при (например, в плазме) частота электромагнитной волны и диэлектрическая проницаемость . Показатель преломления для таких частот становится мнимым. В этом случае образуется стоячая электромагнитная волна, амплитуда которой убывает по экспоненте. Излучение не может пройти через плазму, и происходит полное отражение его в пограничном слое.

Явление нормальной дисперсии лежит в основе призменных спектрографов и спектроскопов.

Дисперсионный спектр отличается от дифракционного тем, что он нелинеен: угол отклонения призмой лучей монохроматического света не пропорционален длине волны.

Для наблюдения нормальной и аномальной дисперсии можно пользоваться методом скрещенных призм (рис.3.5.4), где 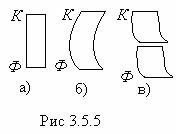А – стеклянная призма; В – призма, изготовленная из исследуемого вещества; Э – экран. Плоскости оснований призмы А и В взаимно перпендикулярны. Призма А освещается параллельным пучком белого света. При прохождение через призмы А и В лучи света отклоняются к основаниям призм. Углы отклонения тем больше, чем больше соответствующие значение n показателя преломления. Если бы призмы В не было, на экране был бы спектр в виде прямоугольной радужной полоски, обусловленный нормальной дисперсией света в стекле. В результате дисперсии света во второй призме спектр на экране криволинеен. На рис.3.5.5а) представлена нормальная дисперсия после призмы А; б) дисперсия в призме В; в) одна из полос поглощения света веществом призмы В находится в области видимого спектра. Сдвиг вправо нижней половины спектра по отношению к верхней обусловлен аномальной дисперсией в пределах полосы пропускания.

 

3.5.2. Модель среды с дисперсией. Фазовая и групповая скорость волны. Волновые пакеты

Строго монохроматическая волна вида

(3.5.6)

представляет собой бесконечную во времени и в пространстве последовательность «горбов» и «впадин», перемещающихся вдоль оси x с фазовой скоростью

. (3.5.7)

С помощью такой волны нельзя передать никакого сигнала, так как каждый последующий «горб» ничем не отличается от предыдущего. Для передачи сигнала нужно на волне сделать «отметку», скажем, оборвав её на некоторое время Δ t. Однако в этом случае волна уже не будет описываться уравнением (3.5.6).

Проще всего передать сигнал с помощью светового импульса (рис.3.5.6).

Согласно теореме Фурье подобный импульс мощно представить как наложение волн вида (3.5.6) с частотами, заключёнными в некотором интервале Δ ω. Суперпозиция волн, мало отличающихся друг от друга по частоте, называется волновым пакетом или группой волн. Аналитическое выражение для группы волн имеет вид

 

(3.5.8)

 

(индекс ω при А, k и α указывает на то, что эти величины для разных частот различны). При фиксированном t график функции (3.5.8) имеет вид, показанный на рис. 3.5.6. С изменением t график смещается вдоль оси x. В пределах пакета плоские волны в большей или меньшей степени усиливают друг друга, вне пакета они практически гасят друг друга.

Соответствующий расчёт даёт, что чем меньше ширина пакета Δ x, тем больший интервал частот Δ ω или соответственно больший интервал волновых чисел Δ k требуется для того, чтобы описать пакет с помощью выражения (3.5.8). Имеет место соотношение

Подчеркнём, что для того, чтобы суперпозицию волн, описываемую выражением (3.5.8), можно было считать группой волн, необходимо соблюдение условия Δ ω << ω₀ .

В недиспергирующей среде все плоские волны, образующие пакет, распространяются с одинаковой фазовой скоростью υ. Очевидно, что в этом случае скорость движения пакета совпадает с υ и форма пакета со временем не изменяется. Можно показать, что в диспергирующей среде пакет с течением времени расплывается – ширина его увеличивается. Если дисперсия невелика, расплывание пакета происходит не слишком быстро. В этом случае пакету можно приписать скорость u, под которой понимается скорость, с которой перемещается центр пакета, т. е. точка с максимальным значением Е. Эту скорость называют групповой скоростью. В диспергирующей среде групповая скорость u, отличается от фазовой скорости υ (имеется в виду фазовая скорость гармонической составляющей с максимальной амплитудой, иными словами – фазовая скорость для доминирующей частоты).

Ниже мы покажем, что в случае, когда dn/dλ₀ <0, групповая скорость оказывается меньше фазовой (u<υ); в случае, когда dn/dλ₀ >0, групповая скорость больше фазовой (u>υ).

На рис. 3.5.7 показаны «фотографии» волнового пакета для трёх последовательных моментов времени t₁, t₂ и t₃ . Рисунок выполнен для случая, когда u < υ. Из рисунка видно, что наряду с перемещением пакета происходит движение «горбов» и «впадин» «внутри» пакета, причём у левой границы пакета всё время зарождаются новые «горбы», которые, пробежав вдоль пакета, исчезают у его правой границы. В результате, в то время как пакет в целом перемещается со скоростью u, отдельные «горбы» и «впадины» перемещаются со скоростью υ.

В случае, когда u>υ, направления перемещения пакета и движения «горбов» внутри него оказываются противоположными.

Поясним сказанное на примере суперпозиции двух плоских волн с одинаковой амплитудой и разными λ. На рис. 3.5.8 дана «момен­тальная фотография» волн. Одна из них изображена сплошной ли­нией, другая — пунктирной. Интенсивность максимальна в точке А, где фазы обеих волн в данный момент совпадают. В точках В и С обе волны находятся в противофазе, вследствие чего интенсивность результирующей волны равна нулю. Допустим, что обе волны рас­пространяются слева направо, причем скорость «сплошной» волны меньше, чем «пунктирной» (в этом случае dn/dω >0, следователь­но, dn/dλ <0). Тогда место, в котором волны усиливают друг друга,

будет со временем перемещаться влево относительно волн. В ре­зультате групповая скорость окажется меньше фазовой. Если ско­рость «сплошной» волны больше, чем «пунктирной» (т. е. dn/dλ >0), место, в котором происходит усиление волн, будет перемещаться вправо, так что групповая скорость окажется больше фазовой.

Напишем уравнения волн, положив для упрощения формул начальные фазы равными нулю:

Здесь k=ω/υ₁, (k+ Δ k)=(ω+ Δ ω)/ υ₂ . Пусть Δ ω<< ω, соответственно Δ k<< k. Тогда, сложив колебания и произведя преобразования по формуле для суммы косинусов, получим

(3.5.9)

(во втором множителе мы пренебрегли Δ ω по сравнению с ω и Δ k по сравнению с k).

Множитель, стоящий в квадратных скобках, изменяется с х и t гораздо медленнее, чем второй множитель. Поэтому выражение (3.5.9) можно рассматривать как уравнение плоской волны, амп­литуда которой изменяется по закону

.

В данном случае имеется ряд одинаковых максимумов амплитуды, определяемых условием

(m= 0,1,2,...). (3.5.10)

Каждый из этих максимумов можно рассматривать как центр соответствующей группы волн.

Разрешив (3.5.10) относительно x _max, получим

 

 

Отсюда следует, что максимумы перемещаются со скоростью

 

(3.5.11)

Полученное выражение представляет собой групповую скорость для случая, когда группа образована двумя составляющими.

Найдём скорость, с которой перемещается центр группы волн, описываемой выражением (3.5.8). Перейдя от косинусов к экспонентам, получим

 

(3.5.12)

 

( - комплексная амплитуда).

Разложим функцию k _ω= k (ω) в ряд окрестности ω₀:

 

(3.5.13)

Здесь k₀=k (ω₀), (dk/dω) ₀ – значение производной в точке ω₀.

Перейдём к переменной ξ = ω – ω₀. Тогда ω = ω₀ + ξ, dω=dξ. Произведя такую замену в (3.5.11) и подставив выражение (3.5.12) для k_ω, можно написать

 

Мы пришли к уравнению плоской волны с частотой ω₀, волновым числом k₀ и комплексной амплитудой

. (3.5.14)

 

Из (3.6.11) следует, что уравнение

(3.5.15)

связывает время t и координату х той плоскости, в которой комплексная амплитуда имеет заданное фиксированное значение, в частности и такое значение, при котором модуль комплексной амплитуды, т.е. обычная амплитуда A(x,t), достигает максимума.

Приняв во внимание, что 1/(dk/dω)₀=(dω/dk)_0, представим (3.5.15) виде

 

(3.5.16)

 

Из (3.5.16) следует, что место, в котором амплитуда группы волн максимальна, перемещается со скоростью (dω/dk)_0. Таким образом, мы приходим к следующему выражению для групповой скорости:

(3.5.17)

 

 

(индекс 0 пропущен за ненадобностью). Ранее для группы из двух волн было получено аналогичное выражение (см. (3.5.11)).

Напомним, что мы пренебрегли членами высоких порядков малости в разложении (3.5.9). В этом приближении форма волнового пакета со временем не изменяется. Если учесть дальнейшие члены разложения, то для амплитуды получается выражение, из которого следует, что ширина пакета со временем растёт – волновой пакет расплывается.

Выражению для групповой скорости можно придать другой вид. Заменив ω через υk (см. (3.5.11)), представим (3.5.17) следующим образом: . Далее напишем Из соотношения λ =2π/k вытекает, что dλ/dk = -2 π/k² = - λ/k. Соответственно

dυ/dk= - (dυ/dλ)(λ/k). Подставив это значение в (3.5.17), получим

 

.

Из этой формулы видно, что в зависимости от знака dυ/dλ групповая скорость u может быть как меньше, так и больше фазовой скорости υ. В отсутствии дисперсии dυ/dλ=0 и групповая скорость совпадает с фазовой.

Максимум интенсивности приходится на центр группы волн. Поэтому в тех случаях, когда понятие групповой скорости имеет смысл, скорость переноса энергии волной равна групповой скорости.

Понятие групповой скорости применимо только при условии, что поглощение энергии волны в данной среде невелико. При значительном затухании волн понятие групповой скорости утрачивает смысл. Такой случай имеет место в области аномальной дисперсии. В этой области поглощение очень велико, и понятие групповой скорости оказывается неприменимым.

 

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: