 |
Развертка цилиндра вращения
|
|
|
|
ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ
Пример выполнения работы 2листа А3, 1 лист А4.
Задача 1
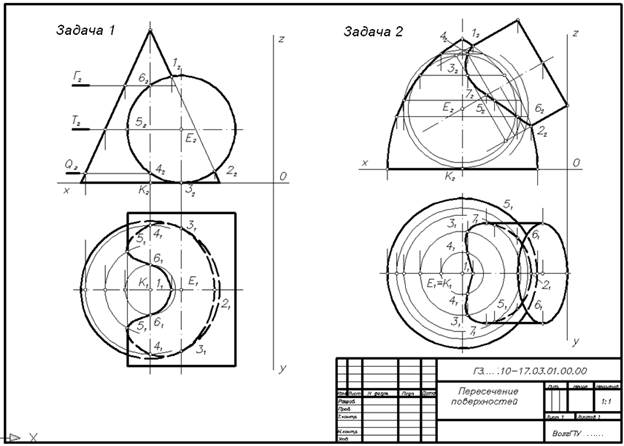
Построить линию пересечения конуса вращения с цилиндром вращения. Оси поверхностей вращения – взаимно перпендикулярные проецирующие скрещивающиеся прямые. Данные для своего варианта взять из табл.1.
Указания к решению задачи 1.
Вычертить условие. В левой половине листа формата А3 намечают оси координат и из табл. 1 берут согласно своему варианту величины, которыми задаются поверхности конуса вращения и цилиндра вращения. Определяют центр (точка К) окружности радиуса R основания конуса вращения на горизонтальной координатной плоскости. На вертикальной оси на расстоянии h от плоскости уровня и выше ее определяют вершину конуса вращения.
Осью цилиндра вращения является фронтально-проецирующая прямая точки Е, основаниями цилиндра являются окружности радиуса R1. Образующие цилиндра имеют длину равную 3 R1,и делятся пополам фронтальной меридиональной плоскостью конуса вращения.
Решение этой задачи упрощается, так как поверхность цилиндра фронтально-проецирующая. Фронтальная проекция линии пересечения совпадает со следом цилиндра на фронтальную плоскость. Точки 1, 2, 3, 5 являются опорными в линии пересечения. Промежуточные точки определяются способом секущих плоскостей. В качестве секущих плоскостей выбирают плоскости параллельные горизонтальной плоскости проекций.
Одноименные проекции точек соединяют с учетом их видимости плавными кривыми и получают проекции искомой линии пересечения.
Все вспомогательные построения сохранять.
Таблица1
| № вар. | К | R | h | Е | R1 | |||||
| x | y | z | x | y | z | |||||
Задача 2
|
|
|
Построить линию пересечения закрытого тора с поверхностью наклонного цилиндра вращения. Заданные поверхности имеют общую фронтальную плоскость симметрии. Данные для своего варианта взять из табл.2.
Указания к решению задачи 2.
В правой половине формата А3 намечают оси координат и из таблицы 2, согласно своему варианту берут заданные величины, которыми определяются поверхности тора и цилиндра вращения. Определяют по координатам положение точки Е, то есть точки пересечения вертикальной оси тора с наклонной осью цилиндра вращения радиуса r = 2R /3.
|
|
|
Главным меридианом поверхности тора является замкнутая линия, состоящая из двух пересекающихся на оси вращения дуг окружностей радиуса 2R и отрезка прямой – проекции экваториальной параллели, представляющей собой окружность с центром в точке К и радиусом R в плоскости уровня xOz.
Точки пересечения главных меридианов относятся к характерным точкам. Дополнительные точки определяем способом вспомогательных концентрических сфер. Центр этих сфер находится в точке пересечения осей этих поверхностей. Определяются Rmin, Rmax и промежуточные R, R1, и т.д. Сферы пересекают поверхности по окружностям. Фронтальные проекции этих окружностей изображаются отрезками прямых линий, которые пересекаются в точках, являющихся фронтальными проекциями точек искомой линии пересечения поверхностей.
Горизонтальные проекции точек линии пересечения строят по принадлежности параллелям тора. Особо обратить внимание на построение точек линии пересечения поверхностей принадлежащих образующим цилиндра, которые являются очерком на горизонтальной плоскости проекций. Полученные точки соединяют плавной кривой с учетом видимости. Соблюдать толщину линий. Вспомогательные линии сохранить.
Таблица 2
| № вар. | К | E | R | δ | ||||
| x | y | z | x | y | z | |||
|
|
|
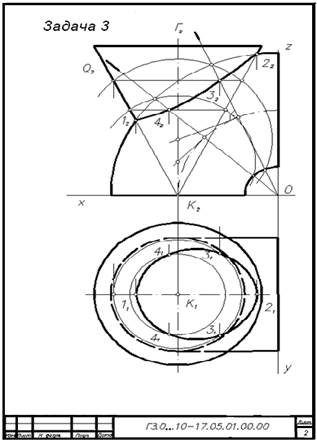
Задача 3 – построить линию пересечения конуса с поверхностью открытого тора. Данные для своего варианта взять из табл.3.
Указания к решению задачи 3.
На формате А4 намечают оси координат и из таблицы 3 согласно своему варианту берут величины, которыми задают поверхности конуса вращения и тора.
Определяют по координатам точку К в плоскости уровня xOy как вершину конуса вращения. Она же является и центром образующей окружности радиуса r поверхности открытого тора. Ось конуса вращения – вертикальная прямая, проходящая через точку К. Высота конуса вращения h, а радиус основания R. Ось поверхности открытого тора совпадает с осью координат y. Тор ограничен координатными плоскостями xOy и yOz.
Для решения задачи применяется способ секущих сфер с переменным центром – способ эксцентрических сфер. Заданные поверхности имеют общую плоскость симметрии. Оси поверхностей не пересекаются. Каждая из поверхностей имеет круговое сечение.
При построении линии пересечения определяем характерные точки – точки пересечения главных меридианов. Затем определяем дополнительные точки. Через ось вращения поверхности кольца провести проецирующую плоскость. Она пересекает кольцо по окружности. Центр сферы, пересекающей кольцо по окружности, находится на перпендикуляре, восстановленном из центра такой окружности к секущей проецирующей плоскости.
Чтобы конус вращения пересекался вспомогательной секущей сферой по окружности, необходимо, чтобы центр такой сферы находился на оси конуса вращения. Этим центром будет точка пересечения перпендикуляра с осью конуса вращения. Такая вспомогательная секущая секущая сфера пересекает кольцо и конус по окружностям, фронтальные проекции которых - отрезки прямых. Эти отрезки, пересекаясь, дают фронтальные проекции точек пересечения поверхностей. Горизонтальные проекции этих точек определяются по принадлежности их к параллелям конуса. Полученные точки соединяют кривой с учетом видимости.
|
|
|
Таблица 3
| № варианта | К | R | h | r | ||
| x | y | z | ||||
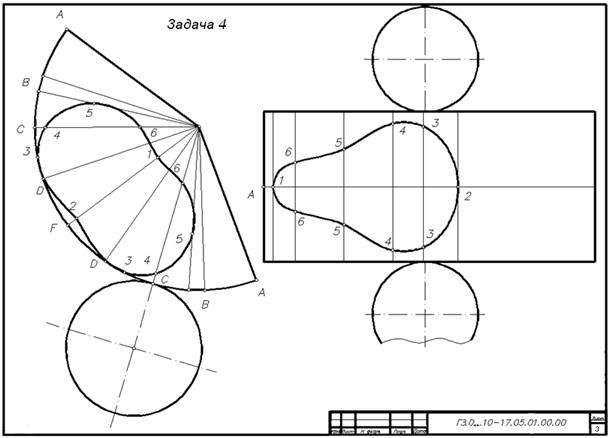
Задача 4 – для задачи 1построить развертки пересекающихся цилиндра вращения с конусом вращения. Показать на развертках линии их пересечения.
Указания к решению задачи 4.
Для построения разверток необходимо выполнить вспомогательные построения: деление окружности основания цилиндра и конуса на 12 частей; построение образующий конуса через полученные точки пересечения поверхностей и определение их натуральных величин. Эти построения выполняются на чертеже задачи 1.
Развертка цилиндра вращения
На листе формата А3 выбирают горизонтальную прямую линию и на ней спрямляют линию нормального сечения цилиндра вращения – окружность радиуса R1. Строят развертку боковой поверхности цилиндра. На развертке проводят прямолинейные образующие, проходящие через точки пересечения цилиндра с конусом. Эти точки отмечают на соответствующих образующих и соединяют плавной кривой линией. Полная развертка цилиндра вращения представляется разверткой боковой поверхности и основаниями – окружностями радиуса R1.
Развертка конуса вращения
Разверткой поверхности конуса вращения является круговой сектор с углом a=R/ (L×360), где R – радиус окружности основания конуса вращения; L – длина образующей.
|
|
|
На развертке конуса вращения строят прямолинейные образующие, проходящие через точки линий пересечения конуса вращения с цилиндром вращения. Полученные точки соединяют плавными кривыми. Полная развертка конуса вращения представляется разверткой боковой поверхности и основанием – окружностью радиуса R.
Основной толстой линией обвести развертки боковых поверхностей, окружности оснований, линии пересечения поверхностей. Все вспомогательные построения выполнить тонкой сплошной линией.
|
|
|


