 |
Ортогональные преобразования отражением
|
|
|
|
Реферат «Введение в численные методы»
Тема: «Методы предварительных эквивалентных преобразований и итерационные методы с минимизацией невязки для решения СЛАУ»
Методы предварительных эквивалентных преобразований
Преобразование вращения
Следующий важный подход к решению алгебраических систем уравнений базируется на применении эквивалентных преобразований с помощью унитарных матриц, сводящем исходную матрицу к эквивалентной ей диагональной.
Смысл этого подхода состоит в том, чтобы последовательно, умножением слева и / или справа на специальные унитарные матрицы, превратить некоторые компоненты исходной матрицы в нуль.
Матрица S называется унитарной, если ее произведение со своей комплексно сопряженной равно единичной матрице. Это означает, что комплексно сопряженная матрица равна обратной матрице:
Известной унитарной матрицей является матрица вращения,которая применяется для поворота на заданный угол вектора, принадлежащего некоторой плоскости, вокруг начала координат. В двумерном случае вектор 
поворачивается на угол 
путем умножения на матрицу
Чтобы сохранить эквивалентность результирующей матрицы при умножении ее на матрицу вращения, необходимо исходную матрицу умножать справа на 
и слева на 
. Умножение же матрицы вращения на вектор дает такой же по величине вектор, но повернутый на заданный угол.
Поворот вектора в многомерном пространстве на произвольный угол можно представить, как последовательность плоских вращений каждой проекции на некоторый угол. Если подобрать угол вращения так, чтобы в плоском повороте одну из проекций вектора совместить с координатной осью, то вторая проекция в этой плоскости становится равной нулю.
|
|
|
Частные повороты вектора в многомерном пространстве с помощью матрицы вращения можно выполнять, если ее расширить до матрицы размера 
следующим образом:
.
Индексы i, j обозначают матрицу вращения, поворачивающую вектор в плоскости 
на угол 
.
Теперь частное эквивалентное преобразование матрицы A вращением на угол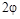 
записываются так:
.
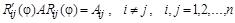Условие превращения в нуль ij- тых элементов симметричной матрицы A можно получить методом неопределенных коэффициентов на двумерной матрице:
.
.
Угол поворота, при котором 
, находится из уравнения
.
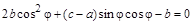Разделив на 
и обозначив 
, 
, получим квадратное уравнение для тангенса требуемого угла поворота
.
Из двух решений для тангенса выбирается такое, чтобы 
. В этом случае 
. Подставив выражение для угла в соотношения для диагональных элементов, после тригонометрических преобразований получаются следующие формулы:
Для получения результирующей матрицы выполнять матричное умножение трех матриц совсем необязательно. Структура матриц вращения вызывает при умножениях изменение только тех элементов исходной матрицы, которые находятся на i- той и j- той строчках и на i- том и j- том столбцах. Изменения представляются суммами элементов, стоящих в строчках и столбцах, умноженных на синус или косинус угла в соответствии с формулами, где j>i:
преобразования строк – 
;
преобразование столбцов –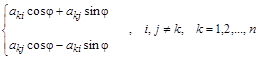 
.
На пересечениях i -й строки и i- того столбца и j -й строки и j- того столбца располагаются соответственно вычисленные выше 
и 
, а на местах ij -того и ji -того элементов вставляются нули.
Для приведения к диагональной матрице необходимо выполнить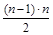 
таких элементарных преобразований.
Ортогональные преобразования отражением
|
|
|
Следующей важной унитарной матрицей, с помощью которой в различных алгоритмах выполняются ортогональные преобразования, являются матрицы отражения. Использование этого инструмента позволяет, например, последовательными эквивалентными преобразова-ниями свести исходную матрицу к верхней треугольной (QR-алгоритмы), трех или двух диагональным и т.д.
Смысл этого подхода состоит в том, чтобы умножением матрицы A слева на специально подобранную унитарную матрицу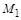 
один из столбцов исходной матрицы (например, 
) преобразовать в вектор, параллельный единичному координатному вектору 
(
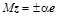или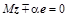 
). Тогда, последовательно подбирая нужные унитарные матрицы 
и соответствующие единичные векторы 
, после n циклов эквивалентных преобразований можно будет получить верхнюю треугольную матрицу:
При выборе в качестве начального вектора 
и умножениях матрицы A на ортогональные матрицы справа в конечном счете можно получить нижнюю треугольную матрицу.
Весь вопрос состоит в том, как формировать унитарную матрицу с заданными свойствами из векторов 
и столбцов 
матрицы A.
Из аналитической геометрии известно, что любые векторы, лежащие в плоскости, взаимно перпендикулярны с ее нормалью, т.е. их проекции на нормаль равны нулю. Последнее эквивалентно равенству нулю скалярных произведений.
Чтобы (k+ 1) – мерный векторный треугольник 
сделать параллельным k- мерной гиперплоскости с нормалью n (вектор единичной длины, перпендикулярный плоскости), необходимо приравнять нулю скалярное произведение: (n, y)=0.
Пусть вектор z не параллелен плоскости, заданной своей нормалью, тогда его проекции на эту плоскость и нормаль соответственно будут представлены векторами 
и 
. Вектор z и вектор зеркально-симметричный ему 
через эти проекции можно выразить так:
Разрешив первое относительно и подставив его в , получим
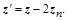
Проекцию вектора можно заменить скалярным произведением (n, z) и подставить в выражение для , выразив тем самым зеркально отраженный вектор через исходный вектор и нормаль гиперплоскости:
Здесь M представляет унитарную матрицу, преобразующую произвольный вектор в зеркально отраженный. В том, что матрица унитарная, нетрудно убедиться, проверив ее произведение со своей комплексно сопряженной:
|
|
|
Выражение для зеркально отраженного вектора позволяет представить нормальный вектор в виде линейной функции от задаваемого вектора z:
Число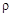 
в знаменателе является нормирующим множителем. Нормальный вектор представляющий гиперплоскость обязан иметь единичную длину. Коэффициент 
, который в общем случае является комплексным числом, необходимо выбрать так, чтобы скалярное произведение 
было больше нуля. Если учесть соотношение для согласованных норм: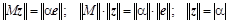 
, то
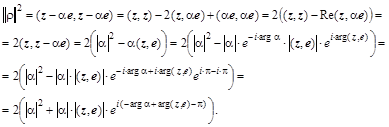
Выбрав 
для комплексных матриц или 
– для действительных матриц, будем иметь
Такое нормирование не нарушает коллинеарности отраженного и единичного векторов:
Рассмотрим пример воздействия ортогонального преобразования на матрицу
.
Приведенная методика получения унитарных (и ортогональных в частности) матриц используется во многих стандартных алгоритмах в качестве инструмента частичного преобразования исходных матриц к двух или трех диагональным, для которых в дальнейшем применяются рекуррентные формулы получения решения уравнений, называемые в литературе методом прогонки для систем с ленточными матрицами.
|
|
|
