Задача «Определение количества товаров на складских филиалах»

Задача по определению уровня запасов при стохастическом распределении

 

При стохастической модели управления запасами требуется оптимизация запасов на начальный период. Рассмотрим вычисления на конкретном примере. Имеются наблюдения по кварталам (n=4) и годам (k=3). Данные представлены в таблице.

Таблица. Распределение сбыта товаров

	Годы
Период n

 

Определяем годовые объемы сбыта и остатки по n-1 периоду по формуле:

B_i = Q₁+Q₂+Q₃+Q₄

B_n-1= B_i- Q_n

Данные сведем в таблицу

	Годы
Период n

 

Затем определяем математическое ожидание по формуле:

 

 

Далее определяем среднеквадратическое отклонение по формуле:

В данном случае σ_i равно:

 

= 24 ед.

Будем считать, что неучтенное изменение цен в будущем δ=0, k=0,1 руб. - затраты на доставку единицы товара, U=0,2 руб. - затраты на хранение товара и λ = 0,8 руб. - убытки от недостатка товара.

Определяем значение функции стандартного нормального распределения:

 

 

Далее определяем по таблице нормального распределения:

Зная математическое ожидание и среднеквадратическое отклонение определяем уровень запаса на начало каждого периода:

	0.00	0.01	0.02	0.03	0.04	0.05	0.06	0.07	0.08	0.09
0.0	0.5000	0.5040	0.5080	0.5120	0.5160	0.5199	0.5239	0.5279	0.5319	0.5359
0.1	0.5398	0.5438	0.5478	0.5517	0.5557	0.5596	0.5636	0.5675	0.5714	0.5753
0.2	0.5793	0.5832	0.5871	0.5910	0.5948	0.5987	0.6026	0.6064	0.6103	0.6141
0.3	0.6179	0.6217	0.6255	0.6293	0.6331	0.6368	0.6406	0.6443	0.6480	0.6517
0.4	0.6554	0.6591	0.6628	0.6664	0.6700	0.6736	0.6772	0.6808	0.6844	0.6879
0.5	0.6915	0.6950	0.6985	0.7019	0.7054	0.7088	0.7123	0.7157	0.7190	0.7224
0.6	0.7257	0.7291	0.7324	0.7357	0.7389	0.7422	0.7454	0.7486	0.7517	0.7549
0.7	0.7580	0.7611	0.7642	0.7673	0.7704	0.7734	0.7764	0.7794	0.7823	0.7852
0.8	0.7881	0.7910	0.7939	0.7967	0.7995	0.8023	0.8051	0.8078	0.8106	0.8133
0.9	0.8159	0.8186	0.8212	0.8238	0.8264	0.8289	0.8315	0.8340	0.8365	0.8389
1.0	0.8413	0.8438	0.8461	0.8485	0.8508	0.8531	0.8554	0.8577	0.8599	0.8621
1.1	0.8643	0.8665	0.8686	0.8708	0.8729	0.8749	0.8770	0.8790	0.8810	0.8830
1.2	0.8849	0.8869	0.8888	0.8907	0.8925	0.8944	0.8962	0.8980	0.8997	0.9015
1.3	0.9032	0.9049	0.9066	0.9082	0.9099	0.9115	0.9131	0.9147	0.9162	0.9177
1.4	0.9192	0.9207	0.9222	0.9236	0.9251	0.9265	0.9279	0.9292	0.9306	0.9319
1.5	0.9332	0.9345	0.9357	0.9370	0.9382	0.9394	0.9406	0.9418	0.9429	0.9441
1.6	0.9452	0.9463	0.9474	0.9484	0.9495	0.9505	0.9515	0.9525	0.9535	0.9545
1.7	0.9554	0.9564	0.9573	0.9582	0.9591	0.9599	0.9608	0.9616	0.9625	0.9633
1.8	0.9641	0.9649	0.9656	0.9664	0.9671	0.9678	0.9686	0.9693	0.9699	0.9706
1.9	0.9713	0.9719	0.9726	0.9732	0.9738	0.9744	0.9750	0.9756	0.9761	0.9767
2.0	0.9772	0.9778	0.9783	0.9788	0.9793	0.9798	0.9803	0.9808	0.9812	0.9817
2.1	0.9821	0.9826	0.9830	0.9834	0.9838	0.9842	0.9846	0.9850	0.9854	0.9857
2.2	0.9861	0.9864	0.9868	0.9871	0.9875	0.9878	0.9881	0.9884	0.9887	0.9890
2.3	0.9893	0.9896	0.9898	0.9901	0.9904	0.9906	0.9909	0.9911	0.9913	0.9916
2.4	0.9918	0.9920	0.9922	0.9925	0.9927	0.9929	0.9931	0.9932	0.9934	0.9936
2.5	0.9938	0.9940	0.9941	0.9943	0.9945	0.9946	0.9948	0.9949	0.9951	0.9952
2.6	0.9953	0.9955	0.9956	0.9957	0.9959	0.9960	0.9961	0.9962	0.9963	0.9964
2.7	0.9965	0.9966	0.9967	0.9968	0.9969	0.9970	0.9971	0.9972	0.9973	0.9974
2.8	0.9974	0.9975	0.9976	0.9977	0.9977	0.9978	0.9979	0.9979	0.9980	0.9981
2.9	0.9981	0.9982	0.9982	0.9983	0.9984	0.9984	0.9985	0.9985	0.9986	0.9986
3.0	0.9987	0.9987	0.9987	0.9988	0.9988	0.9989	0.9989	0.9989	0.9990	0.9990
3.1	0.9990	0.9991	0.9991	0.9991	0.9992	0.9992	0.9992	0.9992	0.9993	0.9993
3.2	0.9993	0.9993	0.9994	0.9994	0.9994	0.9994	0.9994	0.9995	0.9995	0.9995
3.3	0.9995	0.9995	0.9995	0.9996	0.9996	0.9996	0.9996	0.9996	0.9996	0.9997
3.4	0.9997	0.9997	0.9997	0.9997	0.9997	0.9997	0.9997	0.9997	0.9997	0.9998
3.5	0.9998	0.9998	0.9998	0.9998	0.9998	0.9998	0.9998	0.9998	0.9998	0.9998
3.6	0.9998	0.9998	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999
3.7	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999
3.8	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999
3.9	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
4.0	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000

 

Задача по определению уровня запасов при стохастическом распределении

 

При стохастической модели управления запасами требуется оптимизация запасов на начальный период. Рассмотрим вычисления на конкретном примере. Имеются наблюдения по кварталам (n=4) и годам (k=3). Данные представлены в таблице.

Таблица. Распределение сбыта товаров

	Годы
Период n

 

Определяем годовые объемы сбыта и остатки по n-1 периоду по формуле:

B_i = Q₁+Q₂+Q₃+Q₄

B_n-1= B_i- Q_n

Данные сведем в таблицу

	Годы
Период n

 

Затем определяем математическое ожидание по формуле:

 

 

Далее определяем среднеквадратическое отклонение по формуле:

В данном случае σ_i равно:

 

ед.

Будем считать, что неучтенное изменение цен в будущем δ=0, k=0,1 руб. - затраты на доставку единицы товара, U=0,2 руб. - затраты на хранение товара и λ = 0,8 руб. - убытки от недостатка товара.

Определяем значение функции стандартного нормального распределения:

 

 

Далее определяем по таблице нормального распределения:

Зная математическое ожидание и среднеквадратическое отклонение определяем уровень запаса на начало каждого периода:

	0.00	0.01	0.02	0.03	0.04	0.05	0.06	0.07	0.08	0.09
0.0	0.5000	0.5040	0.5080	0.5120	0.5160	0.5199	0.5239	0.5279	0.5319	0.5359
0.1	0.5398	0.5438	0.5478	0.5517	0.5557	0.5596	0.5636	0.5675	0.5714	0.5753
0.2	0.5793	0.5832	0.5871	0.5910	0.5948	0.5987	0.6026	0.6064	0.6103	0.6141
0.3	0.6179	0.6217	0.6255	0.6293	0.6331	0.6368	0.6406	0.6443	0.6480	0.6517
0.4	0.6554	0.6591	0.6628	0.6664	0.6700	0.6736	0.6772	0.6808	0.6844	0.6879
0.5	0.6915	0.6950	0.6985	0.7019	0.7054	0.7088	0.7123	0.7157	0.7190	0.7224
0.6	0.7257	0.7291	0.7324	0.7357	0.7389	0.7422	0.7454	0.7486	0.7517	0.7549
0.7	0.7580	0.7611	0.7642	0.7673	0.7704	0.7734	0.7764	0.7794	0.7823	0.7852
0.8	0.7881	0.7910	0.7939	0.7967	0.7995	0.8023	0.8051	0.8078	0.8106	0.8133
0.9	0.8159	0.8186	0.8212	0.8238	0.8264	0.8289	0.8315	0.8340	0.8365	0.8389
1.0	0.8413	0.8438	0.8461	0.8485	0.8508	0.8531	0.8554	0.8577	0.8599	0.8621
1.1	0.8643	0.8665	0.8686	0.8708	0.8729	0.8749	0.8770	0.8790	0.8810	0.8830
1.2	0.8849	0.8869	0.8888	0.8907	0.8925	0.8944	0.8962	0.8980	0.8997	0.9015
1.3	0.9032	0.9049	0.9066	0.9082	0.9099	0.9115	0.9131	0.9147	0.9162	0.9177
1.4	0.9192	0.9207	0.9222	0.9236	0.9251	0.9265	0.9279	0.9292	0.9306	0.9319
1.5	0.9332	0.9345	0.9357	0.9370	0.9382	0.9394	0.9406	0.9418	0.9429	0.9441
1.6	0.9452	0.9463	0.9474	0.9484	0.9495	0.9505	0.9515	0.9525	0.9535	0.9545
1.7	0.9554	0.9564	0.9573	0.9582	0.9591	0.9599	0.9608	0.9616	0.9625	0.9633
1.8	0.9641	0.9649	0.9656	0.9664	0.9671	0.9678	0.9686	0.9693	0.9699	0.9706
1.9	0.9713	0.9719	0.9726	0.9732	0.9738	0.9744	0.9750	0.9756	0.9761	0.9767
2.0	0.9772	0.9778	0.9783	0.9788	0.9793	0.9798	0.9803	0.9808	0.9812	0.9817
2.1	0.9821	0.9826	0.9830	0.9834	0.9838	0.9842	0.9846	0.9850	0.9854	0.9857
2.2	0.9861	0.9864	0.9868	0.9871	0.9875	0.9878	0.9881	0.9884	0.9887	0.9890
2.3	0.9893	0.9896	0.9898	0.9901	0.9904	0.9906	0.9909	0.9911	0.9913	0.9916
2.4	0.9918	0.9920	0.9922	0.9925	0.9927	0.9929	0.9931	0.9932	0.9934	0.9936
2.5	0.9938	0.9940	0.9941	0.9943	0.9945	0.9946	0.9948	0.9949	0.9951	0.9952
2.6	0.9953	0.9955	0.9956	0.9957	0.9959	0.9960	0.9961	0.9962	0.9963	0.9964
2.7	0.9965	0.9966	0.9967	0.9968	0.9969	0.9970	0.9971	0.9972	0.9973	0.9974
2.8	0.9974	0.9975	0.9976	0.9977	0.9977	0.9978	0.9979	0.9979	0.9980	0.9981
2.9	0.9981	0.9982	0.9982	0.9983	0.9984	0.9984	0.9985	0.9985	0.9986	0.9986
3.0	0.9987	0.9987	0.9987	0.9988	0.9988	0.9989	0.9989	0.9989	0.9990	0.9990
3.1	0.9990	0.9991	0.9991	0.9991	0.9992	0.9992	0.9992	0.9992	0.9993	0.9993
3.2	0.9993	0.9993	0.9994	0.9994	0.9994	0.9994	0.9994	0.9995	0.9995	0.9995
3.3	0.9995	0.9995	0.9995	0.9996	0.9996	0.9996	0.9996	0.9996	0.9996	0.9997
3.4	0.9997	0.9997	0.9997	0.9997	0.9997	0.9997	0.9997	0.9997	0.9997	0.9998
3.5	0.9998	0.9998	0.9998	0.9998	0.9998	0.9998	0.9998	0.9998	0.9998	0.9998
3.6	0.9998	0.9998	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999
3.7	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999
3.8	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999
3.9	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
4.0	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000

 

Задача «Определение количества товаров на складских филиалах»

Складская система торговой компании ООО «Астра» представлена на рисунке 1 и включает в себя центральный склад, расположенный в г. Кемерово и склады, расположенные в городах Кемеровской области. Объем товарного запаса на центральном складе составляет Q = 900 ед. Остатки товарного запаса на складских филиалах равны J, и их размеры по четырем филиалам представлены в таблице

Таблица. Остатки товарного запаса по филиалам

Номер филиала – j
Остатки товарного запаса, J, шт.

 

 

Рис. 1 Схема размещения складов

Суточная потребность складских филиалов, с учетом интенсивности спроса равна D_j и составляет по филиалам: D₁ = 35, D₂ = 125, D₃ = 70, D₄ = 45.

Необходимо определить наличие товаров на складских филиалах – A_j, т.е. А₁, А₂, А₃, А₄. Одновременно следует принять решение о целесообразности создания на центральном складе дополнительных страховых запасов или уровень запасов сохранить прежний.

Методика решения

· Наличие товаров на складских филиалах определяется по формуле:

A = (D_s – J_j/D_j) * D_j,

где D_s интервал снабжения потребителей через филиалы, дней:

D_s = (Q + ∑J_j)/∑D_j = (900 + (40 + 130 + 75 + 50)/ (35 + 125 + 70 + 45) = 4,35.

• Необходимое наличие товаров на складских филиалах, шт.

А₁ = (4,35 – 40/35) * 35 = 113 А₂ = (4,35 - 130/125) * 125 = 566

А₃ = (4,35 – 75/70) * 70 = 230 А₄ = (4,35 – 50/45) * 45 = 146

 

 

Задача «Определение количества товаров на складских филиалах»

Складская система торговой компании ООО «Астра» представлена на рисунке 1 и включает в себя центральный склад, расположенный в г. Кемерово и склады, расположенные в городах Кемеровской области. Объем товарного запаса на центральном складе составляет Q = 900 ед. Остатки товарного запаса на складских филиалах равны J, и их размеры по четырем филиалам представлены в таблице

Таблица. Остатки товарного запаса по филиалам

Номер филиала – j
Остатки товарного запаса, J, шт.

 

 

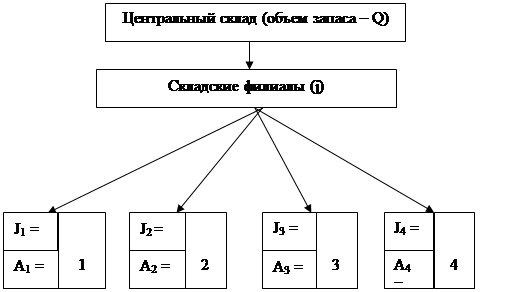
Рис. 1 Схема размещения складов

Суточная потребность складских филиалов, с учетом интенсивности спроса равна D_j и составляет по филиалам: D₁ = 35, D₂ = 125, D₃ = 70, D₄ = 45.

Необходимо определить наличие товаров на складских филиалах – A_j, т.е. А₁, А₂, А₃, А₄. Одновременно следует принять решение о целесообразности создания на центральном складе дополнительных страховых запасов или уровень запасов сохранить прежний.

Методика решения

· Наличие товаров на складских филиалах определяется по формуле:

A = (D_s – J_j/D_j) * D_j,

где D_s интервал снабжения потребителей через филиалы, дней:

D_s = (Q + ∑J_j)/∑D_j =

• Необходимое наличие товаров на складских филиалах, шт.

А₁ = А₂ =

А₃ = А₄ =

 

Поделиться:

Воспользуйтесь поиском по сайту: