Примеры символической записи

УДК 514.18(076)

ББК 22.151.ЗЯ7

М 74

 

 

Рецензент:

В.В. Смагин - доцент, канд. техн. наук

 

Составители: А.Ф. Медведь¹, В.Г. Середа²

 

М 74 Задачи по начертательной геометрии: метод. указания / сост. В.Г. Середа¹, А.Ф. Медведь². – Севастополь: СевГУ, 2016. – 16 с.: ил.

 

Методические указания содержат задачи по начертательной геометрии с примерами их решения. Методические указания предназначены для студентов технических специальностей дневной и заочной формы обучения.

 

Рекомендовано Учебно-методическим советом института в качестве методических указаний по дисциплине «Начертательная геометрия и инженерная графика» для студентов технических специальностей дневной и заочной формы обучения.

 

 

УДК 514.18(076)

 

© Середа В.Г. ¹,

Медведь А.Ф.², сост., 2016

© ФГАОУВО «Севастопольский

Государственный университет», 2016

СОДЕРЖАНИЕ

Введение……………………………………………………………….
1.	Обозначения и символы…………………...…………………….
2.	Примеры символической записи………………...………………
3.	Определения и понятия………………………………………….
4.	Свойства проецирования……………………………..…………
5.	Методические рекомендации…………………………………….
6.	Примеры решения задач….……………………………………..
7.	Задачи для решения………….………………….………….........
	Заключение
	Библиографический список

ВВедение

С целью повышения эффективности обучения студентов произведен отбор ключевых задач по темам курса.

Рекомендуемые задачи по темам лекций приведены в таблице 1.

Таблица 1 – Рекомендуемая последовательность решения задач.

Темы занятий	Задачи для решения
В аудитории	Самостоятельно
Моделирование структуры геометрического объекта	1, 2, 5…8; 13, 14, 18…20; 27, 28	3, 4, 9…12; 15, 16, 21…26; 29…32
Моделирование метрических характеристик объектов	33…36;41, 43	37…40; 42, 44
Моделирование геометрических тел	45, 46, 49…52	47, 48, 53,56
Моделирование сечений геометрических тел	57, 60, 61	57, 58, 62
Моделирование линии пересечения поверхностей	60, 62
Моделирование разверток поверхностей

Отобранный минимум задач рекомендуется для аудиторной и самостоятельной работы студентов при подготовке к сдаче расчетно-графических работ, зачетов или экзаменов.

Обозначения и символы

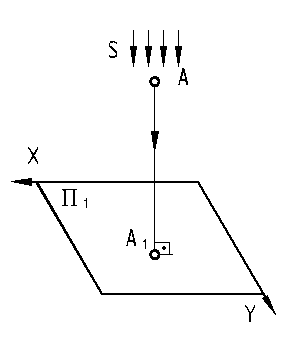
Точка в пространстве обозначается прописными буквами латинского алфавита: A, B, C, D,…или цифрами: 1, 2, 3,…

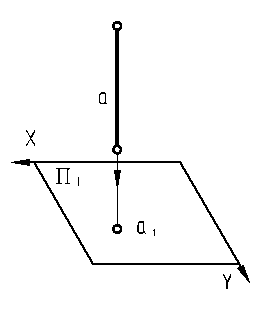
Прямые и кривые линии – строчными буквами латинского алфавита: a, b, c, d,… Линии уровня – строчными буквами: горизонтали – h, фронтали – f, профильные – p.

– направляющие линии (соответственно прямые и кривые) поверхности; – образующие линии (соответственно прямые и кривые) поверхности.

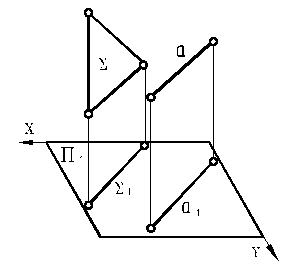
Плоскости и поверхности – прописными буквами греческого алфавита: Σ, Δ, Ρ, Γ,…

Плоские углы – малыми буквами греческого алфавита: α, β, δ, η,…

Принятая система координат OXYZ.

Оси проекций на чертеже X₁₂, Y₁₃, Z₂₃, начало координат O.

Плоскости проекций – буквой Π с индексами 1, 2, 3, 4, 5,… Основные плоскости проекций: Π₁ – горизонтальная, Π₂ – фронтальная, Π₃ – профильная.

Проекции точек, прямых линий, плоскостей, поверхностей, углов – теми же буквами что и в пространстве, с добавлением подстрочного индекса соответствующей плоскости проекций: A₁, a₁, Σ₂, Δ₂ …

Центры и направления проецирования – S, U.

При замене плоскостей проекций новая ось – буквой с соот-ветствующим индексом: X₁₄, Y₂₅ и т.д.

Новое положение точки после одного вращения (перемещения) или после двух соответственно.

Плоскость аксонометрических проекций обозначается буквой Π со знаком штрих – Π'.

Аксонометрические проекции точек, прямых, плоскостей и углов обозначаются теми же буквами со штрихом – A', a', Σ',…

Вторичные проекции имеют внизу индекс прямоугольных проекций, а вверху – штрих: A₁', a₁', Σ₁'.

Аксонометрические оси обозначаются буквами X', Y', Z', начало координат буквой O.

Принятые символы:

º – тождественность; – скрещивание;

Ì – лежит на; – касание;

É – проходит через; Ù – и;

çç – параллельность; Ú – или;

^ – перпендикулярность; = – равно, есть;

Ç – пересечение; Þ – если…, то;

È – соединение;? – построить, определить;

/ – не;! – строим, определяем.

ПРИМЕРЫ СИМВОЛИЧЕСКОЙ ЗАПИСИ

a || b Þ a₁ || b₁ – если прямые параллельны, то одноименные проекции этих прямых параллельны.

f ^ n Þ f₂ ^ n₂ Ù f₁ || x₁₂ – если прямые перпендикулярны (одна – линия уровня, а другая – общего положения), то одна пара их одноименных проекций перпендикулярна.

a Ç b Þ a_i Ç b_i = K_i Ù K₁K₂ ^ x₁₂ – если прямые пересекаются, то одноименные проекции прямых пересекаются в точках, лежащих на одной линии связи, перпендикулярной оси проекций.

? a É A Ù || b – построить прямую, проходящую через точку и параллельную другой прямой.

! a₁ É A₁ Ù || b₁ – строим горизонтальную проекцию прямой, проходящую через горизонтальную проекцию точки, и параллельную горизонтальной проекции другой прямой.

! 1= b Ç AC – строим точку как результат пересечения двух прямых.

! C₁ Ì A₁В₁ – строим горизонтальную проекцию точки на одноименной проекции прямой.

! D Ë D – строим точку, не лежащую на плоскости.

! n ^ D – строим прямую перпендикулярную заданной плоскости.

! h Ì D – строим горизонталь, лежащую на заданной плоскости.

! A Ì a – строим точку, лежащую на заданной прямой.

 

ОПРЕДЕЛЕНИЯ И ПОНЯТИЯ

Аксонометрия– измерение по осям (осеизмерение).

Горизонтальная прямая плоскости – прямая, лежащая на плоскости и параллельная горизонтальной плоскости проекций

Инвариантность– неизменяемость.

Инцидентность – отношение принадлежности между парой геометрических элементов имеющих различную размерность. Инцидентность определяется понятиями "лежит на" и "проходит через".

Комплексный чертеж (эпюр Монжа) – графическая модель объекта, состоящая из связанных между собой ортогональных проекций, лежащих в одной плоскости.

Конкурирующие прямые – прямые, лежащие в плоскости частного положения.

Конкурирующие точки – точки, лежащие на одном проецирующем луче.

Координаты – числа, выражающие расстояние точки от трех плоскостей проекций.

Линейные объекты – прямая, плоскость, многогранник.

Линия наибольшего наклона к горизонтальной плоскости проекций – прямая, лежащая на плоскости и перпендикулярная горизонтальной прямой плоскости.

Линия наибольшего наклона к профильной плоскости проекций – прямая, лежащая на плоскости и перпендикулярная профильной прямой плоскости.

Линия наибольшего наклона к фронтальной плоскости проекций– прямая, лежащая на плоскости и перпендикулярная фронтальной прямой плоскости.

Линия связи – прямая, соединяющая две проекции точки.

Моделирование структуры объекта – построение проекций объекта.

Модель объекта – совокупность элементов, отображающих структуру объекта.

Наглядность чертежа – возможность установить по изображению форму объекта.

Нелинейные объекты– кривые линии и поверхности.

Обратимость чертежа – возможность определения истинных размеров изображенного объекта.

Объект – пространственная фигура, состоящая из геометрических элементов (точек, прямых, плоскостей).

Одноименные проекции – проекции элементов на одну и ту же плоскость проекций.

Ось проекций – линия пересечения двух плоскостей проекций.

Параллельность – отсутствие общих точек у двух прямых, лежащих в одной плоскости, или у прямой и плоскости или у двух плоскостей.

Пересечение – наличие общих точек у геометрических элементов.

Перпендикулярность – свойство двух прямых, прямой и плоскости или двух плоскостей, которые пересекаются друг с другом и образуют в точке пересечения прямой угол (две плоскости в этом случае образуют по линии пересечения двугранный прямой угол).

Плоскости проекций – три грани куба (горизонтальная, фронтальная и профильная плоскости проекций).

Плоскость параллелизма – плоскость, параллельная двум скрещивающимся прямым.

Поверхность– множество положений движущейся линии в пространстве.

Проекции многогранника – проекции его каркаса (с обозначением всех вершин).

Проекция – изображение объекта на плоскости (поверхности).

Развертка многогранника – это совмещение всех граней многогранника с одной плоскостью путем последовательного вращения их вокруг ребер.

Проецирование – процесс получения изображения (проекции) объекта или конструктивная связь между объектом и моделью.

Проецирующий луч – прямая, связывающая точку объекта с её проекцией.

Сечение многогранника – плоский многоугольник, число вершин которого равно числу пересеченных плоскостью ребер.

След прямой– точка пересечения прямой с плоскостью проекций.

След плоскости– линия (прямая) пересечения плоскости с плоскостью проекций.

Структура объекта – схема взаимного расположения элементов объекта.

Фронтальная прямая плоскости – прямая, лежащая на плоскости и параллельна фронтальной плоскости проекций.

Чертеж – графическая модель существующих или воображаемых (проектируемых) объектов.

Элементы геометрического объекта – точки, линии (прямые и кривые), поверхности (плоскости).

Свойства проецирования

Решение задач основано на знании свойств ортогонального проецирования, представленных в таблице 2.

Таблица 2 – Свойства ортогонального проецирования

1. Проекцией точки является точка.

2. Проекцией прямой является прямая (в общем случае).

 

Продолжение таблицы 2

3. Проекцией проецирующей прямой является точка - след прямой (проекция прямой вырождается в точку).	4. Проекция точки, лежащей на прямой, лежит на проекции этой прямой.
5. Проекцией проецирующей плоскости является прямая – след плоскости (проекция плоскости вырождается в прямую).	6. Проекция точки, принадлежащая проецирующей плоскости, лежит на следе плоскости.

 

Продолжение таблицы 2

7. Проекция прямой, принадлежащей проецирующей плоскости, совпадает со следом плоскости.	8. Проекции параллельных прямых параллельны.
9. Следы параллельных проецирующих плоскостей параллельны.	10. Следы проецирующей плоскости и проекция параллельной ей прямой параллельны.

 

Продолжение таблицы 2

11. Следы взаимно перпендикулярных проецирующих плоскостей перпендикулярны друг к другу.	12. След проецирующей плоскости и проекция перпендикулярной к ней прямой взаимно перпендикулярны.
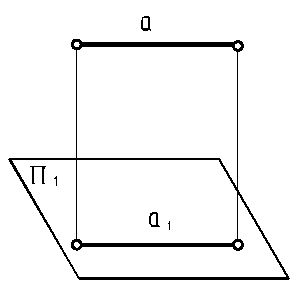
13. Проекции отрезка прямой, не параллельного плоскости проекций, меньше самого отрезка прямой, так как a1 = a cosa.	14. Проекция отрезка, параллельного плоскости проекций, равна самому отрезку (отрезок проецируется в истинную величину).

Продолжение таблицы 2

15. Проекции двух взаимно перпендикулярных пересекающихся или скрещивающихся прямых, одна из которых параллельна плоскости проекций, взаимно перпендикулярны.	16. Следы двух проецирующих плоскостей образуют угол, равный углу между этими плоскостями.
17. След проецирующей плоскости и проекции прямой, параллельной плоскости проекций, образуют угол, равный углу между прямой и плоскостью.	18. Проекции двух пересекаю-щихся или скрещивающих прямых, каждая из которых параллельна плоскости проекций, образуют угол, равный углу между этими прямыми.

Окончание таблицы 2

19. Проекция любой плоской фигуры, параллельной плоскости проекций, равна самой фигуре.

20. Проекция любой выпуклой плоской фигуры является тоже выпуклой.

 

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

Основой для решения задач является усвоение свойств ортогональных (прямоугольных) проекций и овладение способами преобразования проекций. Любая задача сначала решается мысленно в пространстве и только затем переносится на чертеж.

Для успешного решения задач студент обязан к каждому практическому занятию изучить необходимый теоретический материал по конспекту лекций и рекомендуемой кафедрой учебной и методической литературе.

Задачи, рекомендуемые для самостоятельного решения на практических занятиях и дома, следует выполнять в тетради “в клетку”, содержащую 24 листа. Решение всех задач необходимо выполнять только с помощью чертёжных инструментов (циркуля, линейки, угольников, лекал и т.д.) – мягкими карандашами 2М (2В) или 3М (3В). На каждой странице тетради не следует располагать более четырех задач. Проекции заданных геометрических элементов следует обвести толстыми линиями (0,8…0,9 мм) чёрного цвета, линии построения – тонкими линиями (0,3…0,4 мм). Результат решения выделить красным цветом. Все точки и линии, участвующие в построениях, следует обозначать буквами латинского и греческого алфавита, чертежным шрифтом согласно ГОСТ 2.304-81. При построениях недопустимы отклонения в параллельности, перпендикулярности и т.д.

Задачи 18…30 решить без преобразования комплексного чертежа. Задачи 31…44 решить с применением способов преобразования комплексного чертежа.

Каждый студент должен уметь формулировать алгоритмы решения всех задач, предложенных преподавателем для его специальности.

Тетрадь с решёнными задачами студент предъявляет преподавателю, ведущему практические занятия в группе (подгруппе).

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 1. Построить проекции точки, лежащей на плоскости общего положения (рисунок 1а).

Свойство: если точка лежит на плоскости, то проекции точки лежат на одноимённых проекциях прямой плоскости.

Алгоритм решения:

- построить прямую, принадлежащую заданной плоскости (рисунок 1б);

- построить точку, принадлежащую этой прямой (рисунок 1в).

а) б) в)

Рисунок 1

Пример 2. Построить проекции прямой, параллельной заданной прямой общего положения (рисунок 2а).

Свойство: если две прямые параллельны, то одноимённые проекции прямых параллельны.

Алгоритм решения:

- построить проекции прямой параллельно одноимённым проекциям заданной прямой (рисунок 2б).

 

 

 

а) б)

Рисунок 2

Пример 3. Построить проекции прямой общего положения, перпендикулярной к заданной линии уровня (рисунок 3а).

Свойство: если две прямые линии (одна линия уровня, а другая – общего положения) взаимно перпендикулярны, то проекция прямой общего положения перпендикулярна неискажённой проекции прямой линии уровня.

Алгоритм решения:

- построить проекцию прямой общего положения перпендикулярно неискажённой проекции линии уровня (рисунок 3б);

- построить вторую проекции прямой общего положения произвольно (рисунок 3в).

а) б) в)

Рисунок 3

Пример 4. Построить проекции пирамиды по заданным координатам вершин (рисунок 4).

Алгоритм решения:

- построить проекции вершин (точек) пирамиды (рисунок 4а);

- построить проекции ребер (прямых) пирамиды с учетом их видимости (рисунок 4б).

 

а) б)

Рисунок 4

Пример 5. Построить проекции плоскости, проходящей через заданную точку и касающейся поверхности кругового конуса. (рисунок 5а).

Алгоритм решения:

- построить плоскость уровня, проходящую через заданную точку и пересекающую конус по окружности (рисунок б);

- построить касательную к окружности и проходящую через заданную точку (рисунок в);

- построить образующую конуса проходящую через его вершину и точку касания(касательная плоскость определена касательной и образующей) (рисунок 5г).

 

 

а) б) в) г)

Рисунок 5

Пример 6. Построить проекции точки, принадлежащую поверхности сферы (рисунок 6а).

Свойство: если точка лежит на поверхности, то она лежит на линии принадлежащей этой поверхности.

Алгоритм решения:

- построить линию (параллель), принадлежащую поверхности сферы (рисунок 6б);

- построить точку принадлежащую этой линии (рисунок 6в).

 

 

 

а) б) в)

Рисунок 6

Пример 7. Построить проекции линии пересечения проецирующей плоскости с плоскостью общего положения (рисунок 7а).

Свойство: если проецирующая плоскость пересекает плоскость общего положения, то одна проекция линии пересечения совпадает с вырожденной проекцией плоскости.

Алгоритм решения:

- построить точки пересечения проецирующей плоскости с двумя прямыми плоскости (рисунок 7б);

- соединить две полученные точки прямой линией (рисунок 7в).

а) б) в)

Рисунок 7

Пример 8. Построить точку пересечения прямой общего положения с плоскостью общего положения (рисунок 8а).

Свойство: если прямая пересекает плоскость, то одна из проекций прямой пересекает одноименную проекцию конкурирующей с ней прямой

плоскости.

Алгоритм решения:

- построить плоскость-посредник частного положения, проходящую через заданную прямую (проекции прямой и плоскости совпадают) и построить прямую пересечения плоскости-посредника с заданной плоскостью (рисунок 8б);

- построить точку пересечения прямой с плоскостью, как результат пересечения конкурирующих прямых (заданной и прямой пересечения). Определить видимость проекций прямой и плоскости (с помощью конкурирующих точек) на каждой плоскости проекций (рисунок 8в).

 

 

а) б) в)

Рисунок 8

Пример 9. Определить кратчайшее расстояние между двумя точками (рисунок 9а).

Расстояние между двумя точками равно длине отрезка прямой линии, соединяющей эти точки.

Свойство: расстояние между двумя точками проецируется в истинную величину на ту плоскость проекций, по отношению к которой

отрезок, соединяющий эти точки, является прямой уровня.

Алгоритм решения:

- построить проекции расстояния между точками (рисунок 9б);

- преобразовать комплексный чертеж так, чтобы заданная прямая, соединяющая две точки, стала линией уровня (рисунок 9в).

Полученное решение позволяет измерить угол a наклона прямой к горизонтальной плоскости проекций.

Пример 10. Определить угол между пересекающимися прямыми линиями (рисунок 10а).

Свойство: угол между пересекающимися прямыми проецируется в истинную величину на ту плоскость проекций, по отношению к которой эти прямые являются линиями уровня.

Алгоритм решения:

- построить проекции горизонтали и проекции радиуса окружности, по которой перемещается вершина угла (методом прямоугольного треугольника) и определить величину радиуса окружности (рисунок 10б);

- построить истинную величину угла, используя метод вращения вокруг линии уровня (рисунок 10в).

 

 

 

 

а) б в

Рисунок 9

 

 

а) б) в)

Рисунок 10

Пример 11. Построить развертку пирамидальной поверхности (рисунок 11а).

Алгоритм решения (способ триангуляции):

- определить размеры сторон каждой грани (способом прямоугольного треугольника или одним из способов преобразования комплексного чертежа) (рисунок 11б);

- построить композицию смежных граней на плоскости (рисунок 11в);

а) б) в)

Рисунок 11

ЗАДАЧИ ДЛЯ РЕШЕНИЯ

Задачи для решения приведены в таблице 3.

Таблица 3 – Условия задач

1. Определить положение точек относительно плоскостей проекций.

2. Определить положение прямых относительно плоскостей проекций.

Продолжение таблицы 3

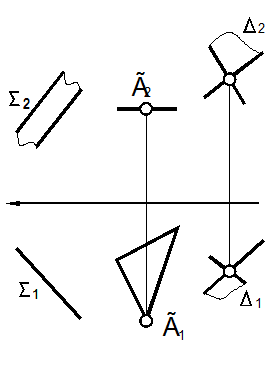
3. Определить положение плоскостей относительно плоскостей проекций.	4. Определить положение пар точек относительно друг друга.
5. Определить взаимное положение точки и прямой по их проекциям.	6. Определить взаимное положение прямых линий по их проекциям. .

 

Продолжение таблицы 3

7. Определить взаимное положение прямой и плоскости по их проекциям.	8. Определить взаимное положение точки и плоскости по их проекциям.
9. Определить взаимное положение плоскостей по их проекциям.	10. Построить три проекции точки по заданным координатам A(10,15,20).

 

Продолжение таблицы 3

11. Построить третью проекцию точки A координатным способом и с помощью постоянной прямой чертежа.	12. Построить по произвольным параметрам проекции точек A, B, C так, чтобы точка A лежала в плоскости P1, точка B лежала в плоскости P2, а точка C была равноудалена от плоскостей проекций P1, P2 и P3.
13. Построить проекции точки, лежащей на заданной прямой линии общего положения.	14. Построить проекции точки, лежащей на заданной проецирующей плоскости.

Продолжение таблицы 3

15. Построить проекции проецирующей плоскости, проходящей через заданную прямую линию общего положения.	16. Построить проекции прямой уровня, лежащей на заданной плоскости общего положения.
17. Построить проекции точки, лежащей на заданной плоскости общего положения.	18. Построить проекции плоскости, параллельной заданной проецирующей плоскости.

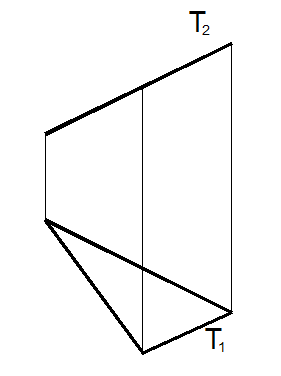
Продолжение таблицы 3

19. Построить проекции прямой, параллельной заданной прямой общего положения.	20. Построить проекции прямой, параллельной заданной плоскости общего положения.
21. Построить проекции прямой, перпендикулярной заданной проецирующей плоскости.	22. Построить проекции линии уровня, перпендикулярной заданной прямой общего положения.

Продолжение таблицы 3

23. Построить проекции прямой, перпендикулярной заданной плоскости общего положения.	24. Построить проекции точки, находящейся от заданной проецирующей плоскости на заданном расстоянии (20 мм).
25. Построить проекции проецирующей плоскости, находящейся от заданной точки, на заданном расстоянии (20 мм).	26. Построить проекции проецирующей плоскости, находящейся от заданной прямой на заданном расстоянии (20 мм).

Продолжение таблицы 3

27. Построить проекции точки пересечения прямой общего положения с проецирующей плоскостью.	28. Построить проекции линии пересечения проецирующей плоскости с плоскостью общего положения.
29. Построить проекции точки пересечения прямой общего положения с плоскостью общего положения.	30. Построить линию пересечения двух плоскостей, занимающих общее положение.

Продолжение таблицы 3

31. Определить расстояние между двумя точками.	32. Определить расстояние между точкой и плоскостью.
33. Определить расстояние между прямой и параллельной ей плоскостью.	34. Определить расстояние между параллельными плоскостями.

Продолжение таблицы 3

35. Определить расстояние между точкой и прямой.	36. Определить величину угла между двумя пересекающимися прямыми.
37. Определить величину угла между двумя скрещивающимися прямыми.	38. Определить величину двугранного угла между двумя пересекающимися плоскостями.

Продолжение таблицы 3

39. Построить проекции точки, находящейся от заданной плоскости общего положения на заданном расстоянии (15 мм).	40. Построить проекции точки, находящейся от заданной прямой на заданном расстоянии (15 мм).
41. Построить проекции прямой общего положения, находящейся от заданной точки на заданном расстоянии (15 мм).	42. Построить проекции прямой общего положения, параллельной заданной прямой и удаленной от неё на заданное расстояние (15 мм).

Продолжение таблицы 3

43. Построить проекции плоскости общего положения, находящейся от заданной точки на заданном расстоянии (15 мм).	44. Построить проекции прямой параллельной плоскости общего положения и находящейся от неё на заданном расстоянии (15 мм).
45. Построить три проекции пятигранной пирамиды по заданному основанию и вершине.	46. Построить три проекции цилиндра вращения по заданному основанию и высоте.

Продолжение таблицы 3

47. Построить три проекции конуса вращения по заданному основанию и вершине.	48. Построить три проекции сферы по заданному радиусу (15 мм) и центру.
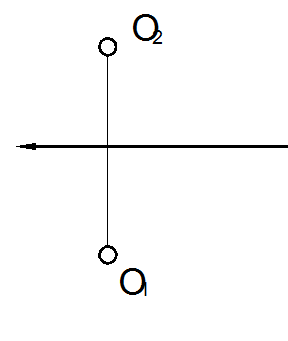
49. Построить две проекции открытого тора, образованного заданной окружностью и осью вращения (горизонтально-проецирую-щей прямой).	50. Построить проекции точек, принадлежащих поверхности призмы (невидимые точки обозначают в круглых скобках).

Продолжение таблицы 3

51. Построить проекции точек, принадлежащих поверхности пирамиды.	52. Построить проекции точек, принадлежащих поверхности сферы.
53. Построить проекции линии, принадлежащей поверхности цилиндра.	54. Построить проекции линии, принадлежащей поверхности конуса.

Продолжение таблицы 3

55. Построить проекции линии, принадлежащей поверхности сферы.	56. Построить проекции винтовой линии, принадлежащей поверхности цилиндра (шаг винтовой линии равен высоте цилиндра).
57. Построить точки пересечения прямой общего положения с поверхностью пирамиды.	58. Построить точки пересечения прямой общего положения с поверхностью конуса.

Продолжение таблицы 3

59. Построить точки пересечения окружности с поверхностью сферы.	60. Построить проекции линии пересечения сферы с горизонтально-проецирующей призмой.
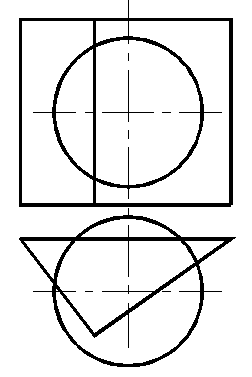
61. Построить проекции линии пересечения (кривую Вивиани) полусферы с фронтально- проецирующим цилиндром	62. Построить линию пересечения конуса с цилиндром (способом концентрических сфер).

Окончание таблицы 3

63. Построить развертку поверхности способом нормального сечения.

 

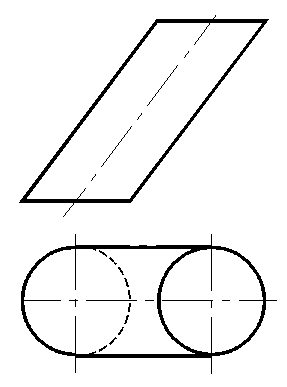
64. Построить развертку поверхности способом триангуляции (треугольников).

ЗАКЛЮЧЕНИЕ

Решая задачи начертательной геометрии, студенты учатся моделировать на чертеже проективные, аффинные и метрические свойства пространственного объекта, а также по известным свойствам проекций выявлять геометрические свойства изображенного объекта и выполнять на чертеже дополнительные геометрические построения.

Умение решать задачи является лучшим критерием оценки глубины изучения программного материала и его усвоения.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК ЛИТЕРАТУРЫ

1. Середа В.Г. Начертательная геометрия. Практикум для студентов: учеб. пособие / В.Г. Середа, А.Ф. Медведь. – Севастополь: Изд-во СевНТУ, 2008. – 122 с.

2. Медведь А.Ф., Середа В.Г. Моделирование структуры геометрических объектов: методические указания к выполнению расчетно-графического задания. – Севастополь: СевГУ, 2016. – 20 с.

3. Медведь А.Ф., Середа В.Г. Моделирование точек и линий на поверхностях геометрических тел: методические указания к выполнению расчет

Поделиться:

Воспользуйтесь поиском по сайту: