Предельные теоремы теории вероятностей

Математические законы теории вероятностей получены абстрагированием реальных статистических закономерностей, свойственных массовым случайным явлениям, которые порождают в своей совокупности случайную величину, подчиненную вполне определенному закону. Массовые случайные явления – рассматриваются как последовательности экспериментов, происходящих при сохраняющемся комплексе условий , или большое число случайных воздействий. Это означает, что конкретные особенности каждого отдельного случайного явления почти не сказываются на среднем результате массы таких явлений. Устойчивость средних и представляет собой физическое содержание закона больших чисел. В теории вероятностей под законом больших чисел понимается ряд математических теорем, в каждой из которых при тех или иных условиях устанавливается факт приближения средних характеристик большого числа экспериментов к некоторым вполне определенным постоянным. Свойство случайных величин в определенных условиях вести себя практически как неслучайные позволяет предсказывать результаты массовых случайных явлений почти с полной определенностью.

Возможности таких предсказаний в массовых случайных явлениях расширяются наличием предельных теорем, касающихся предельных законов распределения. Мы уже говорили, что закон распределения суммы достаточно большого числа случайных величин неограниченно приближается к нормальному распределению при соблюдении некоторых условий, которые содержатся в центральной предельной теореме.

Различные формы закона больших чисел вместе с различными формами центральной предельной теоремы образуют совокупность предельных теорем теории вероятностей.

С некоторыми из них мы уже познакомились.

Так, например, в гл. 2 доказывалось, что при n →∞ p_n→ 0 таким образом, что np_n = , где – фиксированное неотрицательное число, распределение случайной величины сходится к распределению Пуассона

т.е. случайная величина Х рассматривалась как сумма независимых случайных величин Х, имеющих множество значений , и эта сумма аппроксимировалась распределением Пуассона.

При изучении предельных теорем будем рассматривать различные виды сходимости случайных величин.

 

5.1. СХОДИМОСТЬ СЛУЧАЙНЫХ ВЕЛИЧИН

Рассмотрим различные определения понятия предела в теории вероятностей.

Пусть на вероятностном пространстве (Ω, , P) определена последовательность случайных величин X ₁(ω), X ₂(ω),…, X _n(ω),… Для каждого значения Ω получаем числовые последовательности:

которые могут сходиться или расходиться. Множество элементарных событий ω _j, для которых соответствующие числовые последовательности сходятся, образует некоторое событие А Ω.

Тот факт, что последовательность сходится на множестве А Ω, будем записывать: для любых ω А, где случайная величина X (ω) определена на том же вероятностном пространстве (Ω, , P).

Если вероятность множества тех

ω Ω, для каждого из которых числовая последовательность сходится к Х (ω), то последовательность сходится к Х (ω) с вероятностью 1.

Наиболее часто употребляется понятие сходимости по вероятности.

Определение 5.1. Последовательность случайных величин сходится к случайной величине Х(ω) по вероятности и обозначается , если для любого >0

Следовательно, вероятность того, что X_n отличается от X меньше любой заданной величины, близка к единице при достаточно больших значениях n.

Определение 5.2. Последовательность случайных величин сходится к случайной величине X по распределению и обозначается , если для любой точки x, в которой функция F(x) непрерывна .

Функция F(x) непрерывна в точке x в том и только в том случае, если .

Сходимость по распределению используется при аппроксимации одного распределения другим. Примером может служить сходимость биномиального распределения к пуассоновскому, о которой упоминалось выше.

Сходимость по распределению не налагает никаких требований на совместное распределение случайных величин и X.

Следует отметить, что из сходимости по вероятности следует сходимость по распределению , а из сходимости по распределению в общем случае не следует сходимость по вероятности. Сходимость по вероятности и сходимость с вероятностью 1 рассматривается в теоремах закона больших чисел и усиленного закона больших чисел.

 

5.2. НЕРАВЕНСТВО ЧЕБЫШЕВА

 

Чтобы доказать теоремы, относящиеся к закону больших чисел, докажем вначале одно весьма общее неравенство неравенство Чебышева.

Рассмотрим случайную величину X с математическим ожиданием М(Х) и дисперсией D(X). Тогда справедлива теорема, приведенная ниже.

Теорема 5.1. Вероятность того, что величина X отклоняется от своего математического ожидания не меньше любого положительного числа , ограничена сверху величиной , т.е. .

Д о к а з а т е л ь с т в о. Пусть X, дискретная случайная величина, задана рядом распределения:

xi	x1	x2	…	xn	…
pi	p1	p2	…	pn	…

 

Пусть задано некоторое положительное >0. Вычислим вероятность того, что величина X отклонится от своего математического ожидания не меньше чем на , т.е. вычислим вероятность .

________________

Выражение - это сокращенное обозначение для вероятности

 

Ясно, что эта вероятность равна сумме вероятностей p_i для тех значений x_i, для которых отклонения от М(Х) не меньше :

(5.1)

С другой стороны, по формуле (2.5) дисперсия

(5.2)

Если в формуле (5.2) отбросить слагаемые, для которых , то сумма справа уменьшится, так как все члены суммы неотрицательны. Следовательно,

(5.3)

________________

Выражение - это сокращенное обозначение для вероятности

 

 

Выразим в формуле (5.3) через ². Тогда сумма уменьшится:

(5.4)

Но сумма, стоящая в правой части неравенства (5.4) – это вероятность 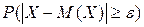. Тогда из формулы (5.4) следует или , что и требовалось доказать.

Если X – непрерывная случайная величина, то знаки суммы следует заменить интегралами.

Заметим, что неравенство Чебышева иногда записывают в виде

.

Пример 5.1. Дана случайная величина X с математическим ожиданием М(Х) и дисперсией σ² (Х). Оценить сверху вероятность того, что величина X отклонится от своего математического ожидания не меньше чем на 3σ (X).

Решение. Используя неравенство Чебышева, пологая = 3σ:

.

Следовательно, вероятность того, что отклонение случайной величины от ее математического ожидания выйдет за пределы трех средних квадратических отклонений, не может быть больше .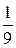

Если воспользоваться правилом трех сигм, то эта же вероятность равна 0,0027. Таким образом, оценка, полученная с помощью неравенства Чебышева, не точная. Важность этого неравенства заключается в его универсальности, и поэтому его используют в основном для доказательства других теорем.

Более точную оценку дает неравенство Колмогорова. Сформулируем его без доказательства.

Теорема 5.2. Пусть X₁,X₂,…,X_n - взаимно независимые случайные величины с математическими ожиданиями , и конечными дисперсиями . Тогда для >0 вероятность того, что одновременно выполняется n неравенств , не меньше чем .

При n= 1 эта теорема сводится к неравенству Чебышева.

Вопросы для самопроверки

1. Вероятность какого неравенства оценивается в неравенстве Чебышева?

2. Как оценить вероятность неравенства ?

3. В чем заключается важность неравенства Чебышева?

4. Что уточняет неравенство Колмогорова?

 

 

5.3. ТЕОРЕМА ЧЕБЫШЕВА

 

Теорема Чебышева – одна из простейших, но наиболее важных форм закона больших чисел.

Рассмотрим случайную величину X, закон распределения которой от эксперимента к эксперименту изменяется. Тогда будем иметь дело с несколькими (n) случайными величинами.

Теорема 5.3. (теорема Чебышева). Если X₁, X₂,…, X_n,… независимые случайные величины с конечными математическими ожиданиями ,и дисперсиями ограниченными одним и тем же числом С, т.е. , то при возрастании n среднее арифметическое наблюденных значений величин , сходится по вероятности к среднему арифметическому их математических ожиданий, т.е. для любого >0

(5.5)

Д о к а з а т е л ь с т в о. Рассмотри величину . Ее математическое ожидание , а дисперсия . Применяя к величине Y неравенство Чебышева, получаем

или

Так как , т о

. (5.6)

Как бы ни было мало >0, переходя к пределу в формуле (5.6) при n→∞, получим

,

что и требовалось доказать.

Из теоремы следует, что среднее арифметическое достаточно большого числа независимых переменных случайных величин (дисперсии которых равномерно ограничены) перестает быть случайной величиной, т.е. оно является устойчивым и сходится по вероятности к определенной неслучайной величине, так как среднее арифметическое математических ожиданий - величина неслучайная.

Если в формуле (5.5) перейти к вероятности противоположного события, получим другую формулировку закона больших чисел:

Частным случаем теоремы Чебышева для одинаково распределенных случайных величин , является

Теорема 5.4 (теорема Хинчина). Пусть X₁, X₂,… - независимые, одинаково распределенные случайные величины, имеющие конечные математические ожидания . Тогда последовательность , где , сходится к m с вероятностью 1, т.е. для любого >0

.

Закон больших чисел может быть распространен и на зависимые случайные величины.

Теорема 5.5 (теорема Маркова). Если для случайных величин X₁, X₂,…

,

то среднее арифметическое наблюденных значений случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий:

для любого >0.

Неравенство Колмогорова (см. теорему 5.2) позволяет доказать теорему Колмогорова, в которой приведены достаточные условия для осуществления усиленного закона больших чисел:

последовательность случайных величин X₁, X₂,…, X_n,… подчиняется усиленному закону больших чисел, если с вероятностью 1 при n→∞ выполняется предельное соотношение

.

Теорема 5.6 (теорема Колмогорова). Если последовательность взаимно независимых случайных величин X₁, X₂,…, X_n,… удовлетворяет условию

,

то она подчиняется усиленному закону больших чисел.

Из теоремыКолмогорова следует утверждение: существование математического ожидания является необходимым и достаточным условием для применимости усиленного закона больших чисел к последовательности одинаково распределенных и взаимно независимых случайных величин.

Усиленный закон больших чисел имеет большое принципиальное значение, так как, согласно этому закону, существует лишь конечное число случаев, когда среднее арифметическое случайных величин будет отличаться от среднего арифметического математических ожиданий.

Вопросы для самопроверки

1. При каких условиях среднее арифметическое наблюденных значений величин , сходится по вероятности к среднему арифметическому их математических ожиданий?

2. Какая теорема является частным случаем теоремы Чебышева? Сформулируйте ее.

3. Сформулируйте закон больших чисел для зависимых случайных величин.

 

 

5.4. ТЕОРЕМЫ, УСТАВЛИВАЮЩИЕ СВЯЗЬ МЕЖДУ ЧАСТОСТЬЮ СОБЫТИЯ И ЕГО ВЕРОЯТНОСТЬЮ

 

Пусть производится n независимых экспериментов, в каждом из которых может появиться или не появиться некоторое событие А. Вероятность появления этого события в каждом эксперименте равна р.

Теорема 5.7 (теорема Бернулли). При неограниченном увеличении числа экспериментов n относительная частота события А, вероятность которого в каждом эксперименте равна р, сходится по вероятности к вероятности р этого события:

для любого >0.

Д о к а з а т е л ь с т в о. Рассмотрим независимые случайные величины – число появлений события А в i -м эксперименте, . Ясно, что эти величины дискретны и заданы следующим рядом распределения:

Xi
рi	р	q

.

 

Значение X_i =1, если событие А наступило в i- м эксперименте, и X_i =0, если событие А не наступило. Математическое ожидание каждой из величин X_i равно , а дисперсия 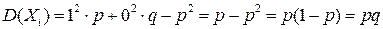. И так как , то (воспользовались неравенством ). Следовательно, дисперсии всех случайных величин X_i ограничены. Кроме того, - числу появлений события А в n независимых экспериментах и ,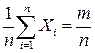

Тогда, применяя теорему Чебышева, получаем

,

что и требовалось доказать.

Теорема Бернулли служит основой интуитивного представления о вероятности и является классическим законом больших чисел.

Более точным и вместе с тем также описывающим основные свойства случайности, которые присущи интуитивному представлению о вероятности, является усиленный закон больших чисел.

Теорема 5.8. Для любого >0 с вероятностью 1 осуществится лишь конечное число событий, для которых выполняется неравенство

.

Если вероятность появления события А изменяется от эксперимента к эксперименту, то справедлива

Теорема 5.9 (теорема Пуассона). При неограниченном увеличении числа независимых экспериментов, в которых событие А появляется с вероятностями р₁, р₂, …, р_n, относительная частота события А сходится по вероятности к средней вероятности события

для любого >0.

Теорема Пуассона является частным случаем теоремы Чебышева, так как , а , где - число появлений события А в i -м эксперименте.

Теорема Пуассона имеет большое принципиальное значение для практического применения теории вероятностей. Дело в том, что нередко вероятностные методы используются для исследования явлений, которые в одних и тех же условиях не могут повториться достаточное число раз, но повторяются многократно при различных условиях, причем вероятности интересующих нас событий в значительной степени зависят от этих условий.

Вопросы для самопроверки

1. Какую сходимость определяет теорема Бернулли?

2. Что определяют независимые случайные величины

3. Что обосновывает теорема Бернулли?

4. Чем отличается теорема Бернулли от теоремы Пуассона?

 

 

5.5. ПОНЯТИЕ ЦЕНТРАЛЬНОЙ ПРЕДЕЛЬНОЙ ТЕОРЕМЫ. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ КАК ПРЕДЕЛЬНОЕ ДЛЯ БИНОМИАЛЬНОГО И ПУАССОНОВСКОГО РАСПРЕДЕЛЕНИЙ

Мы рассмотрели различные формы закона больших чисел, которые утверждают сходимость по вероятности тех или иных случайных величин к определенным постоянным. Причем ни в одной теореме не использовали законов распределения случайных величин. Законы распределения случайных величин рассматриваются в центральной предельной теореме. Согласно центральной предельной теореме, закон распределения суммы достаточно большого числа независимых (или слабо зависимых) слагаемых, каждое из которых в отдельности сравнительно мало влияет на сумму, сколь угодно близко к нормальному закону распределения.

Приведем несколько предельных теорем теории вероятностей без доказательств. При этом случайную величину вида

(5.7)

будем называть нормированной суммой (центрированной случайной величиной).

Теорема 5.10 (теорема Линдеберга- Леви). Если X₁, X₂,…, X_n,… - независимые случайные величины, имеющие один и тот же закон распределения с математическим ожиданием m и дисперсией , то при неограниченном увеличении n закон нормированной суммы сходится по вероятности к нормальному закону с плотностью вероятностей , для которого m=0, =1.

Следует отметить, что и для неодинаково распределенных случайных величин справедлива центральная предельная теорема.

Теорема 5.11 (теорема Ляпунова). Если X₁, X₂,…, X_n,… - независимые случайные величины, имеющие математические ожидания m_i, дисперсии 𝜎_i² и конечные абсолютные центральные моменты третьего порядка , удовлетворяющие условиям

, (5.8)

то при неограниченном увеличении n закон распределения нормированной суммы (5.7) сходится по вероятности к нормальному закону с плотностью вероятностей , для которого m=0, =1.

Смысл ограничения (5.8) состоит в том, чтобы случайные величины были сравнимы по степени своего влияния на рассеивание суммы, т.е. дисперсия каждой случайной величины составляет лишь малую долю общей дисперсии суммы 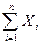. Если бы это было бы не так, то закон распределения суммы 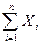определялся бы в основном величиною , для которой дисперсия значительно больше, чем для других случайных величин.

В практических задачах центральную предельную теорему часто используют для вычисления вероятности того, что сумма нескольких случайных величин примет значение, принадлежащее интервалу.

Действительно, пусть , - независимые случайные величины с математическими ожиданиями 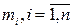, и дисперсиями . Тогда, если каждое из слагаемых равномерно мало влияет на сумму , то закон распределения случайной величины можно считать приближенно нормальным. И вероятность того, что случайная величина примет значение, принадлежащее интервалу , выражается формулой

,

где .

Пример 5.2. Предположим, что распределение числа заменяемых кинескопов за двадцатилетний срок работы телевизора характеризуется математическим ожиданием m =5 и средним квадратичным отклонением σ=1,5. Найти вероятность того, что в течении 20 лет для 10 телевизоров понадобится от 40 до 60 кинескопов.

Р е ш е н и е. Представим общее число заменяемых кинескопов за 20 лет как сумму: , где - число заменяемых кинескопов в i -м телевизоре в течение 20 лет работы.

Так как величины распределены одинаково, можно использовать центральную предельную теорему:

т.е. с вероятностью 0,53 можно утверждать, что в течении 20 лет для 10 телевизоров понадобится от 40 до 60 кинескопов.

Замечание. Следует отметить, что нормальное распределение получается из биномиального распределения и распределения Пуассона при некоторых условиях на n и p.

Пусть случайная величина X подчиняется биномиальному закону с параметрами n и p, тогда можно показать, что при достаточно большом n, если p и q= 1 -p не очень малы, распределение X стремится к нормальному распределению случайной величины 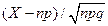. С увеличением n аппроксимация биномиального распределения нормальным улучшается. Этот результат является одной из форм центральной предельной теоремы. Соответствующая нормальная функция распределения будет хорошим приближением к биномиальной, если nр и n (1- р) больше 5.

Распределение Пуассона может быть получено из биномиального. Поэтому если случайная величина X подчиняется распределению Пуассона с параметром , то при n →∞ распределение X будет стремиться к нормальному распределению переменной .

Пример 5.3. Известно, что в среднем 3% электрических лампочек, выпускаемых заводом, бракованные. Найти вероятность того, что из 30 обследуемых лампочек забракованы будут 2. Эту вероятность вычислить с помощью биномиального распределения, его аппроксимацией распределением Пуассона и нормальным распределением.

Р е ш е н и е. Так как р =0,03; q =0,97; n =30; m =2, то:

;

аппроксимация распределения Пуассона:

,

где ;

аппроксимация нормальным распределением: как уже было сказано, биномиальное распределение хорошо аппроксимируется нормальным распределением, имеющим стандартизованную переменную . Итак, и

Найдем стандартизованные значения z: , .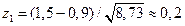
Поэтому

В нашем примере =0,9, поэтому нормальная аппроксимация не совсем удачна.

Вопросы для самопроверки

1. Какая случайная величина называется центрированной случайной величиной?

2. Чем отличается теорема Линдеберга-Леви от теоремы Ляпунова?

3. В чем смысл ограничений в теореме Ляпунова?

4. Если случайная величина подчиняется биномиальному закону (закону Пуассона), то при достаточно большом , распределение стремится к нормальному закону какой величины?

 

 

5.6.ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ МУАВРА-ЛАПЛАСА

Центральная предельная теорема справедлива и для дискретных случайных величин при условии, что рассматриваются их функции распределения. Можно доказать, что если дискретные случайные величины удовлетворяют условиям центральной предельной теоремы, то функция распределения их нормированной суммы

при увеличении n неограниченно приближается к нормальной функции распределения с параметрами m =0 и σ =1, т.е. к функции

или .

Частными случаями центральной предельной теоремы для дискретных случайных величин являются теоремы Муавра—Лапласа.

Известно, что число появлений события А в n независимых испытаниях, вероятность появления которого в каждом испытании равна р, есть дискретная случайная величина X с биномиальным распределением вероятностей. Эту величину X можно представить в виде суммы случайных величин Х_i т.е. , где Х_i — число появлений события А в i -м испытании, . Все случайные величины Х_i имеют одинаковые математические ожидания и дисперсии , а следовательно, и одинаковые квадратические отклонения .

Тогда нормированная сумма Z_n будет иметь вид .

Теорема 5.12 (локальная ). Если 0< р < 1, то равномерно для всех m, удовлетворяющих неравенствам , где а и b - любые заданные постоянные числа, имеет место равенство

.

На практике локальная теорема используется при больших значениях n для вычисления вероятности того, что некоторое событие А наступает m раз в n испытаниях. Эту вероятность находят по приближенной формуле

, (5.9)

где .

Формулу (5.9) применяют и при малых n, когда . Отметим, что функция φ(z) четная, т.е. φ(-z) = φ(z), поэтому при отрицательных значе­ниях аргумента z используют положительные значения z, абсолютное значение которых совпадает.

Для удобства пользования формулой (5.9) составлены таблицы функции , где (см. прил. 4). График этой функции приведен на рис. 5.1. Кривая у = φ(z) называется кривой Гаусса.

 

 

 

 

Рис.5.1

 

Значение теоремы 5.12 заключается в том, что при большом числе испыта­ний n расчет вероятностей по точной биномиальной формуле становится весьма затруднительным и приходится использовать формулу (5.9). Если же речь идет не о вероятности отдельного равенства , а о более важной вероятнос­ти неравенства , то применяют следующую теорему.

Теорема 5.13 (интегральная). Если производится n испытаний, в каждом из которых событие А появляется с вероятностью р, то для любых а и b при n→∞ имеет место соотношение

. (5.10)

Для достаточно больших n используется приближенное равенство

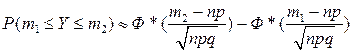, (5.11)

где .

Докажем его.

Д о к а з а т е л ь с т в о. Пусть производится n независимых экспериментов, в каждом из которых с вероятностью р может произойти событие А, и пусть Х₁ — число появлений события А в первом испытании, Х₂ — число появлений события А во втором испытании, X_i - число появлений события А в i -м испытании. Тогда случайная величина - числу появлений события А в n испытаниях. Случайные величины X_i имеют одинаковые законы распределения с математическим ожиданием M(X_i) = р и дисперсией D(X_i)=pq, . Следовательно, закон распределения нормированной суммы неограниченно приближается к нормальному (см. теорему 5.10). Тогда вероятность того, что значения случайной величины Z_n принадлежат отрезку [ а; b ], равна:

, (5.12)

где Ф* (х) — нормальная функция распределения.

Кроме того,

.

Поэтому формулу (5.12) можно переписать в виде

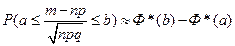
где ,

или

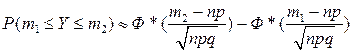
где , что и требовалось доказать.

В формуле (5.11) можно использовать и функцию Лапласа:

.

Для удобства пользования формулой (5.11) составлены таблицы функций Ф*(х) и Ф(х).

Функция Лапласа обладает следующими свойствами: .

Используя эту функцию, формулу (5.11) можно записать:

или, так , то

. (5.13)

По формуле (5.13) вычисляется вероятность того, что событие А в n испытаниях появится от а до b раз.

Пример 5.4. Из каждой поставляемой на оптовую базу партии яиц обследуется 60 шт. Если из этих 60 яиц не менее 3 признаются непригодными, то вся партия переводится в низшую категорию сортности. Вычислить вероятность того, что сортность партии из 500 яиц, в которой 5 % яиц непригодны, будет при таких условиях контроля понижена.

Р е ш е н и е. Если 5 % яиц непригодны, то можно допустить, что вероятность отбора непригодного яйца равна 0,05. Число обследуемых яиц составляет 60 шт. Вероятность Р (Х ≥3), согласно свойствам функции распределения и теореме 5.13, равна:

.

Таким образом, поставщик, который систематически будет поставлять партии, содержащие 5 % непригодных яиц, должен ожидать, что в 50 % случаев поставляемый им товар будет понижен в сортности.

Замечание. Так как случайная величина , где случайные величины Х_i, имеющие множество значений , независимы, , то теорему 5.13 можно сформулировать следующим образом:

Если m — число появлений события А в n испытаниях Бернулли с вероятностью появления события в отдельном испытании р, то при n→∞ равномерно по

Поделиться:

Воспользуйтесь поиском по сайту: