Задачи для самостоятельного решения

I. Теория транспортных процессов

Введение

Транспортная система – это совокупность работников, транспортных средств и оборудования, элементов транспортной инфраструктуры и инфраструктуры субъектов перевозки, включая систему управления, направленная на эффективное перемещение грузов и пассажиров.

Пространственная структура транспортных систем определяется транспортными сетями. Транспортной сетью называется совокупность транспортных связей, по которым осуществляются пассажирские и грузовые перевозки.

Инфраструктура – это физические компоненты транспортной системы, которые занимают фиксированное положение в пространстве и создают транспортную сеть.

Перемещение транспортных средств по транспортной сети образует транспортные потоки, которые характеризуются так называемыми корреспонденциями.

Корреспонденция – вещественный обмен, происходящий от элемента i к элементу j транспортной системы. Таким образом, корреспонденция определяется «путем», имеющим координаты начальной и конечной точек и величину нагрузки в количестве пассажиров или объеме груза.

В автотранспортной системе в качестве транспортных средств используются автомобили. Классификация автотранспортных систем может быть выполнена по разным признакам. Относительно объекта перевозки они могут быть грузовые, пассажирские или грузопассажирские.

Модель транспортной сети может быть представлена в виде графа.

Элементы теории графов

Графом G = { P, Q; I } называется конечная инцидентностная структура, удовлетворяющая двум условиям: 1) P ¹ Æ; 2) каждой прямой инцидентны две точки (возможно, совпавшие).

Здесь P – множество точек, а Q – множество прямых, отношение инцидентности введено на прямом произведении I Í P ґ Q этих множеств. В теории графов точки принято называть вершинами, а прямые – рёбрами. Степенью (или валентностью) вершины в графе называется число рёбер, одним из концов которых является выбранная вершина.

Два графа G ₁ = { P ₁, Q ₁; I ₁} и G ₂ = { P ₂, Q ₂; I ₂} называются изоморфными, если существует биекция f: G ₁ ® G ₂, сохраняющая инцидентность.

Изоморфные графы G ₁ @ G ₂ имеют одни и те же свойства, поэтому их, как правило, не различают с точки зрения теории графов. Изоморфные графы можно изображать одним и тем же рисунком.

Если две различные вершины графа соединены более чем одним ребром, то такие рёбра называются кратными, а граф – мультиграфом. Если же, кроме того, у графа существуют ребра с совпадающими концами (петли), то граф называется псевдографом. Граф без кратных рёбер и петель называют также простым.

& Лемма о рукопожатиях. Сумма степеней всех вершин графа – чётное число, равное удвоенному числу рёбер:

= 2 q.

С графом G, вершины которого помечены числами 1,2,… p, можно связать матрицу A. Для этого достаточно взять каждый элемент a_ij равным числу рёбер, соединяющих вершины с номерами i и j. При этом петля считается за два ребра. Такая матрица называется матрицей смежности графа G.

Эта матрица будет симметрической, а если G – не псевдограф, то на её главной диагонали располагаются нули; если G также не мультиграф, то все элементы матрицы принадлежат множеству {0,1}. Сумма элементов каждой строки (столбца) равна степени соответствующей вершины.

Граф, все рёбра которого ориентированы (то есть, указаны начало и конец каждого ребра, обычно стрелкой), называется ориентированным графом или орграфом. Ориентированные рёбра принято называть дугами. Дуга с началом A и концом B обозначается через AB, если она единственная.

В матрицах смежности помеченных орграфов за a_ij принимают число дуг с началом в вершине i и концом в j. Эти матрицы уже не обязательно будут симметрическими.

Несложно доказать, что графы (орграфы) изоморфны тогда и только тогда, когда их матрицы смежности получаются друг из друга одинаковыми перестановками строк и столбцов.

Путём (или маршрутом) называется конечная последовательность вершин и инцидентных им ребер данного графа, в которой конец каждого ребра, кроме, возможно, последнего, является началом следующего ребра. Если концом последнего ребра является первая вершина, то путь называется замкнутым. Число ребер, входящих в данный путь, называется его длиной. Изолированную вершину можно считать за путь длины, равной 0.

Цепью называется путь, у которого все рёбра различны. Если, кроме того, различны и все вершины, то цепь называется простой. Цепь называется циклом, когда у неё совпадают первая и последняя вершины. Если цепь простая, то и цикл называется простым.

З

адача 12. Являются ли изоморфными графы на рис. 2?

Решение. 1 способ (проверка графов на неизоморфность).

Из определения изоморфных графов следует, что неизоморфные графы отличаются хотя бы одним свойством . Таким образом, нужно сравнить свойства данных графов G и G '.

Пусть p_k (G) – число вершин степени k в графе G. Тогда p ₂(G)= p ₂(G ') = 2 и p ₃(G)= p ₃(G ') = 4. Количество вершин каждой из степеней в графах совпадает.

 

Теперь можно сравнить количество циклов. У графа G имеется два цикла длины 3 (рис. 3), а граф G ' вовсе не имеет таких циклов. Следовательно, графы неизоморфны.

2 способ (использование матриц смежности).

Как говорилось выше, матрицы смежности изоморфных графов получаются друг из друга одинаковыми перестановками строк и столбцов. Или же следует выбрать такую нумерацию вершин графов, чтобы матрицы смежности совпали.

При составлении матриц смежности графов G и G ' нужно следить, чтобы вершинам одного и того же индекса (в графах G и G ' соответственно) достались одинаковые номера (рис. 4).

Получатся следующие матрицы.

В них первая и четвертая строка абсолютно идентичны. Однако невозможно переставить остальные строки матрицы A (G ') так, чтобы получилась матрица A (G). Значит, графы неизоморфны.

3 способ (установление изоморфизма).

Пусть вершины, соответствующие друг другу при изоморфизме f: G ® G', имею

т одинаковые номера. Если номер 1 присвоен вершине степени 2 графа G, то в графе G' этот номер можно дать одной из двух вершин (так как G' симметричен, то безразлично какой). Чтобы сохранялось отношение инцидентности, вершинам, смежным с 1, следует присвоить номера 2 и 3 (рис. 5). При этом получилось, что вершины 2 и 3 инцидентны в графе G, но не инцидентны в G'. Таким образом, установить изоморфизм между этими графами невозможно.<

Простой граф называется полным, если любая его вершина является доминирующей, то есть она смежная со всеми остальными вершинами. Полный граф порядка p обозначается K _p. Степень каждой его вершины равна (p – 1).

Деревом называется связный граф, не содержащий циклов. Любой граф без циклов называется лесом. Таким образом, компонентами леса являются деревья.

Граф называется взвешенным, если каждому его ребру сопоставлено некоторое действительное число.

Задачи для самостоятельного решения

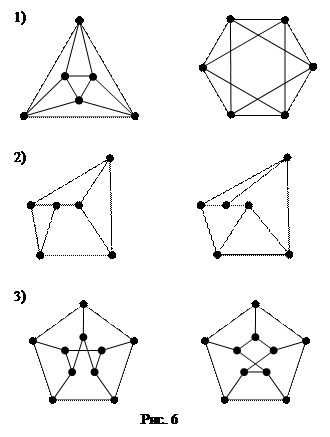
5.1. Среди пар графов на рис. 6 указать изоморфные и неизоморфные.

 

5.2. Нарисовать все простые неизоморфные графы порядка 4.

5.3. Сколько существует неизоморфных деревьев с а) 3 вершинами, б) 4 вершинами, в) 5 вершинами, г) 6 вершинами?

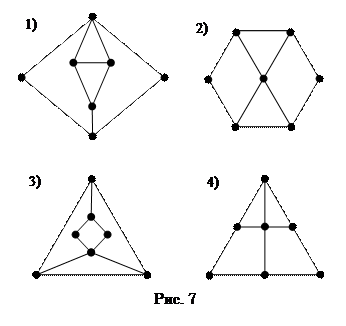
5.4. Какие из графов на рис. 7 являются изоморфными?

5.5. Найти матрицы смежности графов на рис. 8.

 

5.6. Нарисовать графы по их матрицам смежности. Найти степени всех вершин.

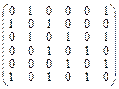1) ; 2) ; 3) .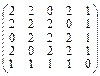

Задача 15.В нашем лесу каждый занимается своим делом: одни плетут корзины, другие ловят рыбу. Ремеслу мы научились друг у друга. Кот учился у Выдры, Ёж – у Зайца, Лиса у Волка, а Мышь у Ежа. Бобёр учил Волка и Выдру, Заяц – Белку, а Барсук – Зайца. Бобер был учеником Медведя, а Ёж – учителем Дятла. Лучше всех плел корзины Ёж. Чем занимались Заяц, Дятел, Волк и Лиса? Кто из зверей нашего леса раньше всех научился ловить рыбу, а кто плести корзины?

Решение. При решении задачи следует обратить внимание на то, что здесь указаны разные отношения: быть учителем (учить) и быть учеником (учиться). Но, поскольку эти отношения взаимообратные, то в рассматриваемой ситуации можно заменять одно отношение другим. Поэтому, прежде чем строить орграф, необходимо договориться, в каком направлении следует изображать все стрелки, соединяющие вершины орграфа: от учителя к ученику или наоборот.

Пусть для примера выбрано отношение: быть учителем. В этом случае стрелка между соответствующими точками будет направлена от учителя к ученику (граф, отражающий условия данной задачи, изображён на рис. 20). <

8.4. В некоторой стране любые два города связаны друг с другом непосредственно одним из следующих средств сообщения: автобусом, поездом или самолетом. Известно, что не существует города, обеспеченного всеми тремя видами транспорта, в то же время не существует трех городов, связанных одним и тем же средством сообщения. Найти наибольшее возможное число городов в этой стране.

8.5. Из компании в 70 человек каждые двое знакомых имеют в той же компании одинаковое число знакомых, а каждые двое незнакомых – разное число знакомых. Доказать, что найдётся человек, имеющий не менее 11 знакомых.

 

Основные транспортные задачи решаемые с помощью теории графов:

1) задача о максимальном потоке: два узла соединены транспортной сетью; каждому ее ребру соответствует определенная пропускная способность (по числу транспортных единиц, объему груза или количеству пассажиров). Требуется найти максимальный поток, который можно пропустить по сети из одного пункта, называемого источником s, в другой, называемый стоком S. (алгоритм Форда-Флакерсона);

2) поиск кратчайшего пути в графе: найти наикратчайший путь (по ребрам графа) от вершины i до вершины j. (метод Минти – расстановки весов)

3) построение дерева наименьшего веса.

Поделиться:

Воспользуйтесь поиском по сайту: