Общая схема исследования функции

ФУНКЦИИ, ИХ СВОЙСТВА И ГРАФИКИ

 

Функция - соответствие между множествами X иY, при котором каждому элементу множества X соответствует один и только один элемент множества Y.

 

X-область определения функции Д(f)

Y- область значения функции,Е(f)

x X-аргумент y Y-функция

y=f(x)-обозначение функции

 

Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.

 

Область значений функции - это множество всех действительных значений y, которые принимает функция.

 

График функции y=f(x) - множество точек (x;y)на координатной плоскости XOY, абсциссами которых являются значение аргумента, а ординатами соответствующие значение функции.

 

Способы задания функции:

 

a) Аналитический способ – задание с помощью формулы (или формул), самый распространительный в математике.

b) Графический способ - задание с помощью графика.используется в пауке и технике, экономике и др.иногда график – единственно возможен способ задания функции, например при пользовании приборами(барограф, термограф, кардиограф и др.)

c) Табличный способ – задание функции с помощью таблицы. Этот способ определяет функцию не полностью и не дает наглядного изображения; характерен для экспериментальных наук;экономике и др.

d) Словесный способ- задание функции словами.

e) Смешанное задание функции - использование 2-х или 3-х названных выше способов задания функции.

 

Основные свойства функции
	Функция y=f(x) называется возрастающей, если для х1:х2 Д(у), для которых х1<x2 выполняется f(x1)<f(x2) (рис.1)
	Функция y=f(x) называется убывающей, если для х1;х2 Д(у), для которых Х1<Х2 выполняется f(х1)>f(х2) (рис.2).
	Функция y=f(х) называется монотонной, если она возрастает или убывает.
	Функция y=f(x) называется четной. Если для x Д(у) -Х так же Д(у) и выполняется равенство f(-x)=f(x) Геом. График четной функции симметричен относительно оси ординат (OY) (рис. 3).
	Функция y=f(x) называется нечетной, если для x Д(у) - х так же Э Д(у) и выполняется равенство f(-x)=-f(x) Геом. График четной функции симметричен относительно начало координат (рис. 4).
	Функция y=f(x) называется ограниченной сверху, если найдется такое число М, для которого справедливо неравенство: f(x)<M (рис.5)
	Функция y=f(x) называется ограниченной снизу, если найдется такое число М, для которого справедливо неравенство: f(x)>M (рис. 6)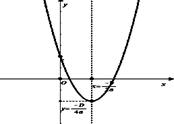
	Функция y=f(x) называется ограниченной, если она ограничена и сверху и снизу
	Корень функци и - значение аргумента, при котором функция обращается в 0. Геом. корни функции- точки пересечения функции с осью OX (рис.7)
	Промежутки знакопостоянства функции y=f(x) - числовые промежутки значений аргумента x,при котором функция имеет один и тот же знак
	Функция y=f(x) называется обратимой, если она имеет обратную ней функцию. Условия существования обратной функции: Каждому значения x единственным образом соответствует значение y и наоборот -каждому значению y соответствует единственное x. Построение обратной функции: 1.Построить y=f(x) 2.Проверить по условиям существования, есть ли функция, обратная к данной 3. Построить биссектрису I и III координатного углов, т.е. y=x 4.Отразить по симметрии относительно y=x функцию y=f(x) (рис.8)
	Функция y=f(x) называется непрерывной на промежутке (a;b), если она непрерывна в каждой точке этого промежутка, т.е. каждому (рис.9)
	Точкой разрыва функции y=f(x)называется значение аргумента x0, при котором функция не является непрерывной (рис. 10)

 

 

Общая схема исследования функции

 

1. Область определения функции y = f(x), т.е. Д(f).
2. Область значения функции y = f(x), т.е. Е(f).
3. Наибольшее и наименьшее значение f(x).
4. Корни функции.
5. Промежутки знакопостоянства.
6. Четность и нечетность функции.
7. Монотонность функции.
8. Периодичность функции.
9. Ограниченность функции.
10. Обратимость функции.
11. Непрерывность функции.

 

 

Пример: Определить свойства функции y = x² – 4.

 

	1. Д(у) = (-∞;∞)
2. E(y) = [ -4; ∞)
1. Наибольшего значения нет. Наименьшее y = - 4
4. y = 0; x2 – 4 = 0; x = ±2
5. y > 0 при x y < 0 при
6.у – четная, т.к. график симметричен относительно оси ОУ
7.у – возрастает при х∈(0;+∞) и убывает при х∈(-∞;0)
8. не периодическая
9.ограничена снизу
10. не обратима
11. непрерывна

 

Поделиться:

Воспользуйтесь поиском по сайту: