 |
Уравнение теплового баланса
|
|
|
|
Нагревание и охлаждение
Этот процесс характеризуется изменением температуры системы. Количество теплоты определяется по формуле
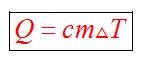
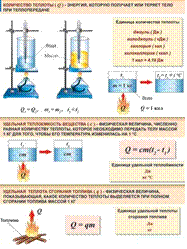Удельная теплоемкость вещества с измеряется количеством теплоты, которое необходимо для нагревания единицы массы данного вещества на 1К=10С. Для нагревания 1кг стекла или 1кг воды требуется различное количество энергии. Удельная теплоемкость - табличная величина.
Теплоемкость вещества (тела) С - это количество теплоты, которое необходимо для нагревания тела без учета его массы на 1К.
При вычислении ΔT договоримся из большей температуры вычитать меньшую. Тогда количество теплоты будет всегда положительной величиной. Это уменьшает вероятность ошибки при сложении количества теплоты, выделяющегося при охлаждении с количеством теплоты выделяющимся, например, при кристаллизации.
Горение
Количество теплоты, которое выделяется при сгорании вещества
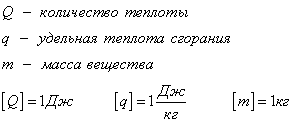
Удельная теплота сгорания табличная величина.
Плавление и кристаллизация
Плавление - переход вещества из твердого состояния в жидкое. Обратный переход называется кристаллизацией.
Энергия, которая тратится на разрушение кристаллической решетки вещества, определяется по формуле
Значение удельной теплоты плавления можно найти в таблицах.
Парообразование (испарение или кипение) и конденсация
Парообразование - это переход вещества из жидкого (твердого) состояния в газообразное. Обратный процесс называется конденсацией.
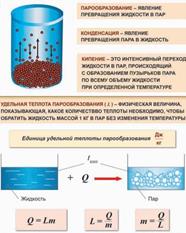
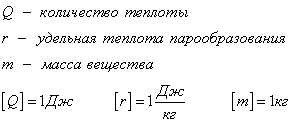
Удельная теплота парообразования табличная величина.
Уравнение теплового баланса
Если мы рассмотрим изолированную (нет обмена энергией с окружающей средой) систему тел (твердых или жидких), в которой теплообмен может совершаться только между телами входящими в эту систему, то в результате этого процесса в системе установится тепловое равновесие. Температуры всех тел станут одинаковыми и равными некоторому значению Q.
|
|
|
В процессе теплообмена тела, начальные температуры которых больше Q («горячие» тела), будут отдавать свою энергию, а тела, у которых начальные температуры меньше Q, - получать энергию.
Из закона сохранения энергии (т.к. система изолированная) следует, что количество теплоты, потерянное телами с более высокой температурой, будет равно количеству теплоты, приобретенному телами с более низкими температурами.
Qотд=Qполуч где Qотд - количество теплоты, отданное «горячими» телами; Qполуч - количество теплоты, полученное «холодными» телами.
Это уравнение носит название уравнения теплового баланса. А положение, что количество теплоты, потерянное «горячими» телами, равно количеству теплоты, приобретенному «холодными телами» называется законом теплообмена.
В приведенном выше подходе при составлении уравнения теплового баланса мы везде из большего значения температуры должны вычитать меньшее, тогда значения количеств теплоты всегда были положительными.
«Виртуальный банк» тепла
Довольно часто встречаются задачи в которых требуется найти конечную температуру системы. Хорошо, если из контекста понятно в каких агрегатных состояниях будут находиться вещества после прекращения теплообмена. Тогда уравнение теплового баланса удается записать с первого раза. Но если непонятно что получится в конце (например, вода, смесь вода+лед, смесь вода+пар и т.п.) то приходится либо по очереди перебирать все варианты, находить конечную температуру и смотреть не противоречит ли она равновесному состоянию данной системы (к примеру, смесь вода+лед не будет существовать при +150С), либо поэтапно сравнивать отдельные количества теплоты и все время отвечать на вопросы… «хватит - не хватит?».
|
|
|
Но есть и другой подход, основанный на замечательном свойстве закона сохранения энергии – связывать начальные и конечные состояния системы независимо от процесса перехода. Если система сложно шла к установлению теплового равновесия, то всегда можно представить весь переход в виде набора из нескольких элементарных процессов, расчет которых не вызывает труда. Пусть даже эти элементарные процессы заведомо не могут протекать в реальной жизни. Окончательный результат (в данном случае, конечная температура) все равно окажется такой же, как и в случае одного сложного процесса.
Поясним на примере. Пусть произошла разгерметизация кастрюли-скороварки с перегретой водой. Масса воды в кастрюле m. Начальная температура T (T>Tкипения). Какая часть воды испарится?
Сколько тепла забирает/отдает перегретая вода не совсем ясно, зато мы умеем рассчитывать, сколько выделит эта вода при остывании и сколько тепла потребуется для испарения некоторой массы при температуре кипения. Тогда предложим схему некоторого виртуального банка тепла. Предположим, что вся перегретая вода остынет до температуры кипения. Тогда она выделит некоторое Q1=mc(T-Tкипения). Временно «отправим» это тепло в банк. Теперь найдем сколько потребуется тепла для испарения некоторой массы mп при температуре кипения? Это легко Q2=mпL. Если система теплоизолирована, то тепло на испарение мы можем взять только из виртуального банка. Q1=Q2. Окончательно 
. Такой прием особенно выгодно применять в случае теплообмена большого количества тел (и нагревателей), для процессов со сложной и непонятной физикой теплообмена и для поиска конечной температуры системы.
В последнем случае, можно мысленно охладить всю систему до температуры самого холодного тела. Посчитать выделившееся при этом тепло и пустить его на нагревание сразу всей системы.
|
|
|
