 |
Измерение длины, ширины и толщины пластинки штангенциркулем
|
|
|
|
Лабораторная работа № 2
ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ ТВЕРДОГО ТЕЛА
Цель работы: ознакомиться с устройством и принципом действия штангенциркуля. Научиться пользоваться этим прибором для определения плотности твердых тел правильной геометрически формы.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Плотностью вещества ρ называется физическая величина, численно равная массе единицы объёма этого вещества.
Если тело однородное, то плотность определяют как отношение массы тела m к занимаемому им объёму V:
 . (I)
. (I)
В СИ плотность измеряют в кг/м³. Иногда в литературе встречаются внесистемные единицы: г/см³, кг/л, т/м³.
Из формулы (1) видно, что для определения плотности необходимо измерить его массу и объём. Массу тела измеряют взвешиванием, а для определения объема существуют различные методы. Если тело имеет правильную геометрическую форму, то измеряют его линейные размеры, а затем по соответствующей формуле вычисляют его объём V.
ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
Для измерения линейных размеров тел используют штангенциркуль и микрометр, основной частью которых является нониус – устройство, позволяющее увеличивать точность отсчёта, даваемую этими приборами. Нониусы бывают линейные, круговые и спиральные. Поскольку нониусы часто встречаются не только в штангенциркуле и микрометре, но и в других, в частности, в оптических приборах, необходимо познакомиться с принципом действия этого устройства.
Нониус
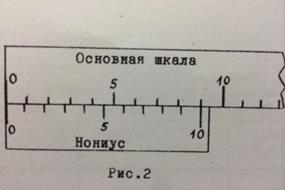
Нониусом называется подвижная вспомогательная шкала, с помощью которой производят отсчет долей делений основной шкалы измерительных приборов. Деление нониуса выбирают обычно так, чтобы n делениям нониуса соответствовало (n – 1) делений основной шкалы (рис.2).
|
|
|
Если обозначить цену деления нониуса через αн, а цену деления основной шкалы через αм, то можно написать:

или
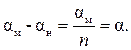 (4)
(4)
Величину α называют точностью нониуса. Если, например, основная шкала разделена на миллиметры (т.е. цена деления основной шкалы 1мм), а нониус имеет 10 делений, то мера точности его будет α = 0,1 мм.
Обычно длина деления нониуса αн короче каждого из делений основной шкалы на α = αм/ n. Поэтому при совпадении нулевого штриха нониуса с каким либо штрихом основной шкалы (назовем этот штрих условно тоже «нулевым») «к» - й штрих нониуса отстает от ближайшего последующего штриха основной шкалы на к α = к αм/ n (рис. 2)
Передвинем нониус так, чтобы «к»-й штрих нониуса совпал с некоторым штрихом основной шкалы (рис. 3). Тогда нулевой штрих нониуса отодвинется от «нулевого» штриха основной шкалы на расстояние
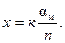
На рис. 3 имеем: αм = 1, n = 10, к = 7, х = 0,7.
Если перед нулевым штрихом нониуса ближайший штрих основной шкалы не нулевой, а соответствует делению m, то положение нуля нониуса на основной шкале определяется величиной (см. рис. 4):
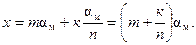 (5)
(5)
Таким образом можно сформулировать следующее правило: длина предмета, отсчитываемая по нониусу равна целому числу делений основной шкалы, находящимся перед нулевым штрихом нониуса ( m αм), сложенному с точностью нониуса, умноженной на номер «к»-го штриха нониуса, который совпадает со штрихом основной шкалы.
На рис. 4 имеем: m = 7 (по основной шкале), к = 6. Следовательно,
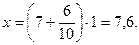
Погрешность, возникающая при измерении с помощью нониуса, определяется неточным совпадением " к "-го штриха нониуса с делением основой шкалы. Величина этой погрешности, очевидно, не может быть больше 0,5 αм/ п, так как если бы она больше, то мы произвели бы отсчет по следующему делению.
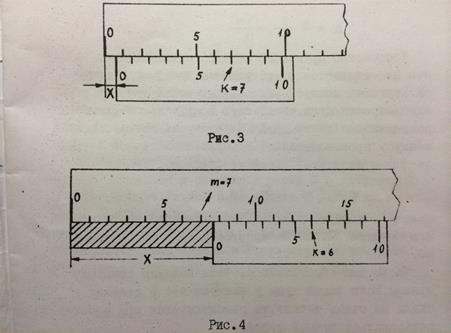
Таким образом, можно сказать, что погрешность нониуса равна половине его точности:
|
|
|
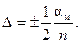 (6)
(6)
Штангенциркуль

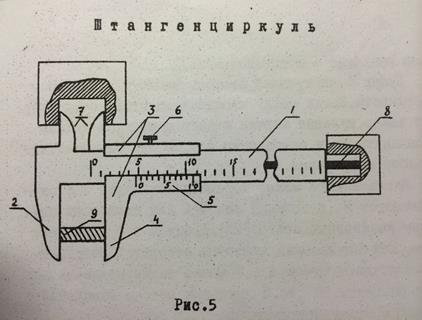
Штангенциркулем называют прибор, служащий для измерения наружных и внутренних размеров тел, а также глубин отверстий (рис.5). Он позволяет измерять длину, толщину, внутренний и внешний диаметры отверстий с точностью от 0,02 до 0,1 мм.
Штангенциркуль состоит из штанги 1 с миллиметровыми делениями и подвижной рамки 3 с нониусом 5 и закрепляющим винтом 6. На штанге и рамке имеются губки 2 и 4. Губки имеют или закругленные концы (как на рис.5) или заостренные, которыми можно делать разметочные штрихи и окружности на измеряемых деталях (по этой причине прибор и получил общее название - штангенциркуль).
Губки с внутренней стороны имеют гладкие поверхности. Когда между плоскостями губок отсутствует зазор, нулевые штрихи штанги и нониуса должны совпадать. Если совпадения нет, то это означает, что прибор неисправен.
Вдоль штанги может перемещаться рамка 3 с глубиномером 8 (выдвижная линейка для измерения глубины несквозных отверстий). Губки 4 и 7 позволяют измерять внутренние диаметры отверстий. Заостренными концами губок 4 и 7 можно также пользоваться' для разметки. На рис. 5 показаны методы измерений с помощью штангенциркуля.
Для проведения измерений прибор берут в правую руку, а измеряемый предмет удерживают левой рукой. Перед началом измерений необходимо убедиться, что нулевые деления штанги и’ нониуса совпадают.
Надавливая на рамку 3 большим пальцем правой руки, плотно зажимают предмет между выступами губок. Затем закрепляют винт 6 и производят отсчет но нониусу. При достаточном навыке винт 6 можно и не закреплять.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Упражнение 1
Измерение длины, ширины и толщины пластинки штангенциркулем
1. Для полученной подлежащей измерению прямоугольной пластинки с известной массой m запишите в отчет
эту массу m = _________ и погрешность её измерения Δ m = ___________.
2. Проведите с помощью штангенциркуля 5 измерений длины a, 5 измерений ширины b и 5 измерений толщины пластинки в разных ее местах и результаты измерений занесите в таблицу 1.
3. По данным таблицы вычислите средние значения измеренных размеров < a >, < b > и <h> пластинки, а также абсолютные (Δ a,Δ b и Δ h) и относительные (ε a,ε b и ε h) погрешности измерений.
|
|
|
Таблица 1
| № п/п | a, мм | Δ a, мм | (Δ a)2, мм2 | b, мм | Δ b, мм | (Δ b)2, мм2 | h, мм | Δ h, мм | (Δ h)2, мм2 |
| 1. | |||||||||
| 2. | |||||||||
| 3. | |||||||||
| 4. | |||||||||
| 5. | |||||||||
| <a>= | - | 
| <b>= | - | 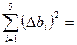
| <h>= | - | 
|
4. Выберите надежность Р = 0,95. Для этого значения надежности и для n = 5 измерений коэффициент Стьюдента tp,n = 2,78.
Абсолютная погрешность:
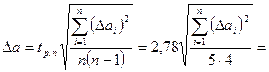
Аналогично
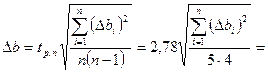
и

Относительные ошибки:
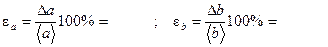 ;
; 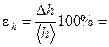
Запишите окончательные результаты измерений в виде:
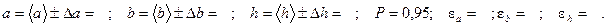 .
.
Упражнение 2
|
|
|


