Задачи по теме: Расчёт параметров оптических кабелей

ОСНОВНЫЕ ВЕЛИЧИНЫ, ФОРМУЛЫ И

ТАБЛИЧНЫЕ ДАННЫЕ

Показатель преломления среды:

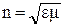, (1)

где e – диэлектрическая проницаемость среды;

m – магнитная проницаемость среды.

 

Относительная разность показателей преломления «сердцевина-оболочка» оптического волокна (ОВ):

, (2)

где n_с – показатель преломления сердцевины ОВ; n_о – показатель преломления оболочки оптического волокна, на практике D = 0,003 – 0,01.

Показатель преломления сердцевины градиентного ОВ меняется от сердцевины к оболочке:

, (3)

где r – текущий радиус;

n_c – максимальное значение показателя преломления на оси ОВ;

D - относительная разность показателей преломления «сердцевина-оболочка»;

a – радиус сердцевины;

u – показатель степени изменения профиля показателя преломления, равный 1 для треугольного профиля, 2 – для параболического, ¥ - для прямоугольного.

Показатель преломления сердцевины градиентного оптического волокна (при параболическом распределении показателя преломле­ния):

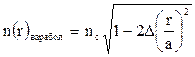, (3а)

где n_с – показатель преломления в центре сердцевины;

r – текущий радиус;

а – радиус сердцевины волокна.

Для направляемых мод в ОВ выполняется условие полного внутреннего отражения:

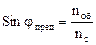. (4)

В кварцевых ОВ для систем связи значение j_пред полного внутреннего отражения составляет на практике 85-86^о.

Числовая апертура. Апертура - это угол между оптической осью и одной из образую­щих светового конуса, попадающего в торец волоконного световода, при котором в световоде в ОВ выполняется условие полного внутреннего отражения. Этот телесный угол q_А определяет числовую апертуру

(5)

где n_oc – показатель преломления окружающей среды у торца волокна.

Числовая апертура для ступенчатых световодов (при n_oc = 1):

. (6)

Для градиентных световодов локальная числовая апертура:

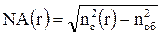. (6а)

Нормированная (характеристическая) частота – обобщённый параметр ОВ:

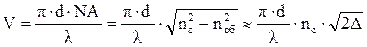, (7)

где d – диаметр сердцевины волокна; l – длина волны.

 

Таблица 1 – Соотношения нормированной частоты, длины волны и радиуса сердцевины для n_c=1,49 и при различных значениях коэффициента преломления оболочки

l, мкм	Значение V при d, мкм
Dn= nc - nоб (nc=1,49)
0,003	0,01	0,003	0,01	0,003	0,01	0,003	0,01
0,85	2,7	5,1	3,3	6,2	16,5	32,1		63,9
1,00	2,3	4,2	2,8	5,2		27,1		54,3
1,30	1,7	3,2	2,2	4,1		21,4		41,8
1,55	1,46	2,7	1,82	3,4	9,1	17,6

 

 

Одномодовый режим реализуется, если нормированная частота V < 2,405. Чем меньше разность Dn = n_с – n_об, тем при большем радиусе световода и меньшей длине волны обеспечивается одномодовый режим.

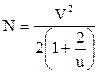Число распространяемых мод:

(8)

 

где u –показатель степени изменения профиля

показателя преломления (ППП), равный

1 для треугольного профиля, 2 – для параболического, ¥ - для прямоугольного.

Для ступенчатого профиля показателя преломления u = ∞ и число распространяемых мод:

. (9)

Для градиентных световодов с параболическим профилем u = 2 и число распространяемых мод:

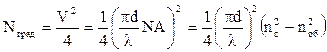. (9а)

Затухание в оптических волокнах. Потери излучения в световодах измеряются отношением интенсивности выходного (прошедшего) и входного (падающего) световых потоков:

,

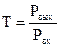где P_вых – мощность прошедшего через ОВ светового потока; P_вх – мощность входящего (падающего) на ОВ светового потока.

Экспериментально потери излучения в волоконных световодах принято выражать в децибелах на единицу длины волокна 1 км (линейные потери):

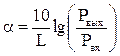(10)

Затухание является важнейшим параметром оптических ка́белей. Затухание обусловлено собственными потерями в волоконном свето­воде a_с и дополнительными потерями, так называемыми кабельными, a_к, обусловленными скруткой, а также деформацией и изгибами оптических волокон при наложении покрытий и защитных оболочек в про­цессе изготовления ОК:

. (11)

Собственные потери волоконного световода состоят из потерь по­глощения молекулами кварца и потерь рассеяния вследствие изменения направления рас­пространения лучей на нерегулярностях и их высвечивания в окру­жающее пространство:

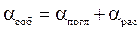. (11а)

Часть мощности поглощается также и посторонними примесями (a_прим), выделяясь в виде джоулева тепла. Примесями могут являться ионы металлов (никель, железо, кобальт и др.) и гидроксильные группы (ОН), приводящие к появлению резонансных всплесков затухания.

В результате суммарные потери в ОК определяются из выражения:

(11б)

Затухание за счёт поглощения связано с потерями на диэлектриче­скую поляризацию, линейно растет с частотой, существенно зависит от свойств материала оптического волокна (tgd) и рассчитывается по формуле:

, дВ/км, (12)

где n_с – показатель преломления сердцевины ОВ;

tgd – тангенс угла диэлектрических потерь материала сердцевины ОВ (для кварцевого материала tgd» 10^-11);

l – длина волны, мкм.

Потери на поглощение растут линейно с уменьшением частоты.

Потери релеевского рассеяния обусловлены неоднородностями ма­териала волоконного световода, расстояния между которыми меньше длины волны, и тепловой флуктуацией показателя преломления. Потери на рассеяние, называемое рэлеевским, определяются:

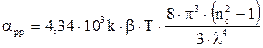(13) или подробнее , (13а)

где К_р – коэффициент рассеяния (для кварца равный 0,8 (мкм⁴×дБ)/км),

l – длина волны, мкм,

k=1,38 ×10^-23 Дж/К – постоянная Больцмана,

b=8,1×10^-11 м²/Н – коэффициент сжимаемости для кварца,

Т»1500 К – температура затвердевания стекла при вытяжке.

Потери на рэлеевское рассеяние определяют нижний предел потерь, присущих волоконным световодам. Поте­ри на рассеяние (в отличие от потерь на поглощение) растут с изменением частоты существенно быстрее - по закону F⁴. Потери на рэлеевское рассеяние сильно проявляются в коротковолновой области спектра.

Поглощение в ИК области уменьшаются с ростом частоты и определяются показательной функцией:

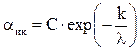, (14)

где С и k – постоянные коэффициенты, характерные для поглощающей среды. Для кварца С = 0,9; k = (0,7 … 0,9) ×10^-6 м.

В кварцевом световоде существует три окна прозрачности: первое окно про­зрачности на длине волны 0,85 мкм, второе окно прозрачности на длине волны 1,3 мкм и третье окно прозрачности на длине волны 1,55 мкм. Наименьшее затухание имеется в третьем окне прозрачности. Второе и третье окна прозрачности разделены между собой так называемым пиком водяного поглощения с максимумом на длине волны 1383 нм.

Затухание в оптических кабелях. Дополнительное затухание, обусловленное кабельными потерями (a_к), состоит из суммы, по крайней мере, семи видов парциальных ко­эффициентов затухания:

(15)

где a¢₁ – возникает вследствие приложения к ОВ термомеханических воз­действий в процессе изготовления кабеля;

a¢₂ – вследствие температурной зависимости коэффициента преломле­ния материала ОВ;

a¢₃ – вызывается микроизгибами ОВ;

a¢₄ – возникает вследствие нарушения прямолинейности ОВ (скрутка);

a¢₅ – возникает вследствие кручения ОВ относительно его оси (осевые напряжения скручивания);

a¢₆ – возникает вследствие неравномерности покрытия ОВ;

a¢₇ – возникает вследствие потерь в защитной оболочке ОВ.

Дополнительные потери определяются в основном процессами рассеяния энергии на неоднородностях, возникающих вследствие перечисленных влияний, и частично увеличением потерь на поглощение энергии. Причинами увеличения потерь на поглощение являются остаточные осевые и поперечные напряжения в ОВ, могущие возникнуть при изготовлении кабеля.

В ряде случаев микроизгибы могут существенно влиять на прирост a_k. Значение потерь на одном микроизгибе может изменяться в пределах 0,01 – 0,1 дБ. Приращение затухания от микроизгибов a¢₃ зависит от мелких локальных нарушений прямолинейности ОВ, характеризуемых смещением оси ОВ в поперечных направлениях на участке микроизгиба. Основными причинами появления микроизгибов явля­ются локальные неосесимметричные механические усилия различного происхождения, приложенные к очень малым участкам ОВ. К микроизгибам следует отнести такие поперечные деформации ОВ, для кото­рых максимальное смещение оси ОВ соизмеримо с диаметром сердце­вины волокна. Особенностями микро-изгибов является то, что они, как правило, многочисленны, а расстояние между соседними микроизгиба­ми существенно больше их размера. Общий вклад потерь, создаваемых микроизгибами, может быть значителен. Вследствие микроизгиба происходит ограничение апертурного угла излучения, распростра­няющегося по ОВ, и часть энергии излучается из ОВ. Зависимость приращения затухания от микроизгибов a¢₃ можно определить из вы­ражения:

(16)

где k₃ = 0,9 – 1,0; N_н - число неоднородностей в виде выпуклостей со средней высотой y_н на единицу длины; а - радиус сердцевины; b - диаметр оптической оболочки; D – относительное значение показателя преломления; n₁ и n_{2 –} показатели преломления сердцевины и оболочки; Е_о и Е_с - модули Юнга оболочки и сердцевины ОВ.

Затухание в местах соединений оптических волокон. Внешние потери. В отличие от традиционных кабелей затухание в сростках ОВ мо­жет достигать больших величин, соизмеримых с километрическим затуханием. На затухание сростка большое значение оказывает попе­речное смещение и смещение осей. На рис. 1 приведены возмож­ные варианты дефектов сопряжения ОВ (радиальное, угловое и осе­вое смещение).

 

Рис.1 Радиальное d (а), угловое q (б) и осевое S (в) смещение ОВ

 

При радиальном смещении дополнительные потери определяются из формулы:

(17)

где d – диаметр сердцевины ОВ; d – радиальное смещение ОВ.

При угловом смещении дополнительные потери определяются из формулы:

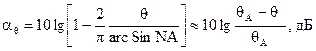(18)

где q_А - апертурный угол волокна; q – угловое смещение ОВ.

При осевом смещении дополнительные потери определяются из формулы:

(19)

где q_А - апертурный угол волокна; d - диаметр сердцевины ОВ; S - осевое смещение ОВ.

Приведенные выражения достаточно хорошо согласуются с экспериментальными, если значения d, q и S достаточно малы (d / d £ 1). Наиболее жесткие требования предъявляются при ради­альном и угловом смещении. Наличие зазора между торцами волокон существенно меньше влияет на потери.

Потери, вызванные различием показателей преломления оптических сред (френелевские потери):

(20)

Внутренние потери. Производство оптических волокон оставляет некоторые допуски на воспроизводимость их параметров. Потери в ОВ обусловлены различием: числовых апертур, диаметров сердцевины, диаметров модового поля, некруглостью, неконцентричностью сердцевины/оболочки.

Если передающее ОВ имеет бо́льшую числовую апертуру, чем приёмное, то возникают потери. Для ступенчатых ОВ:

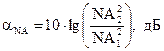(21)

Когда диаметр передающего ОВ больше, чем диаметр приёмного, то возникают потери:

(22)

Допуски на числовую апертуру и диаметры различны для разных ОВ.

Суммарные потери в соединении многомодовых ОВ определяются:

(23)

При соединении одномодовых ОВ необходимо учитывать различие диаметров модовых полей. При гауссовом распределении поля диаметр модового поля определяется соотношением:

(24)

где а – радиус сердцевины ОВ, V – нормированная частота.

Дисперсия сигналов в ОВ

 

 

Уширение импульсов в оптическом волокне:

, (25)

где t_вх – ширина импульса на входе; t_вых – ширина импульса на выходе (значения берутся на уровне поло­вины амплитуды импульсов).

Рис. 2.

 

Существует целая группа причин возникновения дисперсии (рис.2). В многомодовых ОВ преобладает модовая дисперсия, которая зависит от типа профиля показателя преломления в используемом волокне.

Модовая (межмодовая) дисперсия возникает в многомодовых волокнах и обусловлена различием времени распространения различ­ных мод в световоде. Модовая дисперсия определяется в основном профилем показателя преломления.

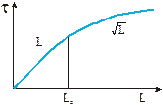Модовая дисперсия зависит от длины ОВ. Длина связи мод - это длина оп­тического волокна, после прохождения которой, в результате взаимно­го преобразования мод на нерегулярностях (обмен энергии между мо­дами и их высвечивание) соотношение между мощностями различных мод становится практически постоянным. Модовая дисперсия в этом случае возрастает уже не по линейному, а по корень-квадратичному закону.

Рис. 3.

 

Модовая дисперсия в многомодовых волокнах со ступенчатым профилем показателя преломления:

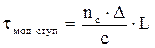при L £ L_c, (26)

при L ³ L_c, (26а)

где D – относительная разность показателей преломления;

n_с – показатель преломления сердцевины;

с – скорость света (с = 3×10⁵ км/с);

L - длина оптического волокна;

L_c – длина связи мод (5–7 км для ступенчатого многомодового волокна).

В градиентных волокнах различные лучи также проходит различ­ный путь. Однако их скорость v=c/n различна. Околоосевые лучи рас­пространяются по короткой траектории, однако в среде со сравнитель­но высоким n, т. е. с малой скоростью, а периферийные лучи - по длинной траектории, но в основном в среде с низким n, т. е. с большой скоростью. В результате модовая дисперсия в градиентных ОВ уменьшается.

Модовая дисперсия в градиентных волокнах:

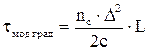при L £ L_c, (27)

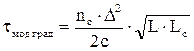при L ³ L_c, (27а)

где D – относительная разность показателей преломления; n_с – максимальное значение показателя преломления сердцевины; с – скорость света (с = 3×10⁵ км/с); L – длина оптического волокна; L _c – длина связи мод (10 – 15 км для градиентных МОВ).

 

Таблица 2. Значения модовой диспер­сии t_мод в ступенчатых и градиентных волокнах для различных длин линии и при различных соотношениях показателей преломления сердцеви­ны и оболочки.

Длина линии L, км	Значение tмод, нс
Ступенчатое ОВ	Градиентное ОВ
Значение D
0,01	0,0 6	0,01	0,006
			2,47	1,09
			3,55	1,58
			4,32	1,91

 

Хроматическая (частотная) дисперсия возникает из-за некогерентности источников излучения и делится на матери­альную и волноводную (иногда выделяют ещё так называемую профильную дисперсию).

Материальная дисперсия определяется частотной зависимостью показателя преломления материала ОВ n = f (l). Уширение импульсов из-за материальной дисперсии:

, (28)

где Dl – ширина спектральной линии источника излучения (равная 0,1 – 4 нм для ЛД и 15 – 80 нм для СИД); с – скорость света; L – длина линии.

Для инженерных расчётов в первом приближении можно использо­вать упрощённую формулу, не учитывающую форму профиля показа­теля преломления (для идеального ступенчатого профиля показателя преломления):

, (28а)

где М(l) – удельная материальная дисперсия.

 

Таблица 3. Типичные значения удельной материальной дисперсии для стандартных кварцевых ОВ.

Длина волны l, мкм	0,6	0,8	1,0	1,2	1,3	1,4	1,55	1,6	1,8
М(l), пс/(нм×км)	-400	-125	-40	-10	+5	+5	+18	+20	+25

 

С увеличением длины волны значение t_мат увеличивается, а затем проходит через нуль и приобретает положительное значение.

Для расчёта хроматической дисперсии используется эмпирическая формула Селмейера (для ОВ с несмещённой дисперсией):

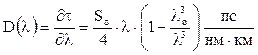(29)

где S_o – наклон дисперсионной кривой, пс/(нм²×км), l_о – длина волны нулевой дисперсии.

 

Волноводная (внутримодовая) дисперсия обусловлена процессами внутри моды. Она характеризуется зависимостью коэффициента распространения моды от длины волны. Являясь составной частью хроматической дисперсии (так же как и материальная дисперсия), волноводная дис­персия зависит от ширины передаваемого спектра частот.

 

Уширение импульсов из-за волноводной дисперсии t_вв находится из выражения:

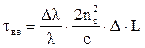(30)

где Dl – ширина спектральной линии источника излучения;

n_c – показатель преломления сердцевины ОВ;

с – скорость света в вакууме;

D – относительная разность показателей преломления;

L –длина линии.

Для инженерных расчётов можно ис­пользовать упрощённую формулу:

(30а)

где В(l) - удельная волноводная дисперсия, значения которой приведены в таблице.

 

Таблица 4. Типичные значения волноводной дисперсии в кварцевых ОВ.

Длина волны l, мкм	0,6	0,8	1,0	1,2	1,3	1,4	1,55	1,6	1,8
В(l), пс/(нм×км)	-5	-5	-6	-7	-8	-8	-12	-14	-16

 

 

Профильная дисперсия проявляется в реальных оптических волок­нах, которые могут быть регулярными (например, с регулярной, гели­коидальной скруткой), нерегулярными (например, нерегулярное изме­нение границы раздела ППП), неоднородными (например, наличие инородных частиц). К причинам возникновения профиль­ной дисперсии относятся поперечные и малые продольные от­клонения (флуктуация) геометрических размеров и формы волокна, например: небольшой эллиптичности поперечного сечения волокна; изменения границы профиля показателя преломления (ППП); осевые и внеосевые провалы ППП, вызванные особенностями технологии из­готовления ОВ.

Продольные флуктуации могут возникать в процессе изготовления ОВ и ОК, строительства и эксплуатации ВОЛС. В ряду случаев про­фильная дисперсия может оказать существенное влияние на общую дисперсию. Профильная дисперсия может проявляться как в многомодовых, так и в одномодовых ОВ. Физически происходит перекачка энергии между направляемыми, оболочечными и излучаемыми волна­ми.

 

Уширение импульсов из-за профильной дисперсии:

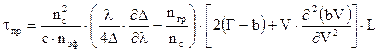(31)

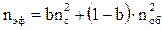
где n_эф – эффективный показатель преломления;

b – нормированная постоянная распространения;

n_гр – групповой показатель преломления сердцевины;

Г – коэффициент локализации по мощности;

V – нормированная частота;

с – скорость света;

D – относительная разность показателей преломления;

L – длина линии;

l – длина передаваемой световой волны.

Это выражение справедливо для одномо­довых волокон при реальной флуктуации границы раздела ППП. При наличии других внешних влияющих факторов её значение может значительно увеличиваться.

Для инженерных расчётов можно использовать упрощённую фор­мулу:

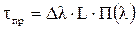(31а)

где П(l) – удельная профильная дисперсия, типичные значения которой представлены в табл.5;

Dl – ширина спектра излучения источника;

L – длина линии.

 

Таблица 5. Типичные значения профильной дисперсии в ОВ.

Длина волны l, мкм	0,6	0,8	1,0	1,2	1,3	1,4	1,55	1,6	1,8
П(l), пс/(нм×км)			-1,5	-5	-2,5	-4	-5,5	-6,5	-7,5

 

Результирующее уширение импульсов за счёт модовой, материальной, волноводной и профильной дисперсий:

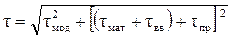(32)

Уширение импульсов возникает не только исключительно при про­хождении сигнала через оптическое волокно, но и за счёт прохождения сигнала через соединители, модулирующие, демодулирующие и дру­гие устройства.

В случае гауссовой формы импульсов все эти прира­щения длительности сигнала суммируются по квадратичному закону:

(33)

где t_вых – длительность импульса на выходе фотоприемника; t_вх – длительность импульса на входе излучателя; t_i – уширение импульса в i-м элементе тракта.

Как правило, наибольшие искажения в сигнал вносит оптический кабель. Поэтому, согласно (27), зная длительность импульсов на входе и выходе тракта, можно рассчитать величину уширения импуль­сов в оптическом кабеле по формуле (20), причем значения t_вых и t_вх берутся на уровне половины амплитуды импульсов.

Критическая частота и критическая длина волны. По оптическим волокнам возможна передача электромагнитных волн длиной меньше критической длины волны. Значения критиче­ской частоты волны и критической длины можно определить из выражений:

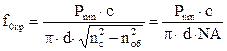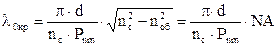, , (34)

где P_nm – значения корней функции Бесселя для различных типов волн; с – скорость света; d – диаметр сердцевины оптического волокна; n_c и n_oб – показатели преломления сердцевины и оболочки.

В этих выражениях параметр P_nm характеризует тип волны (моду). Для критических значений нормированной частоты V_nm = P_nm. Для оценки P_nm следует воспользоваться таблицей 6.

Таблица 6. Значения корней бесселевых функций в зависимости от порядка n и номера корня m.

 

 

n	Значение Pnm при m	Тип волны
	2,405	5,520	8,654	Е0m, Н0m
	0,000	3,832	7,016	НЕ1m
	3,832	7,016	10,173	ЕН1m
	2,445	5,538	8,665	НЕ2m
	5,136	8,417	11,620	ЕН2m

Как видно из таблицы, только одна волна НЕ₁₁ не имеет ограничения по критической частоте.

Расчёт элементов конструкций оптических ка́белей.

Из большого количества разнообразных типов конструкций ОК можно выделить четыре группы: ка́бели концентрической повивной скрутки, ка́бели с профилированным сердечником, плоские ка́бели ленточного типа и ка́бели пучковой скрут­ки.

При механическом расчёте ОК элементы ка́беля рассматривают как систему независимо деформирующих цилиндров, пренебрегая их попе­речным взаимодействием при растяжении вдоль оси кабеля.

Допусти­мое растяжение конструкции ка́беля, состоящей из n элементов, можно оценить по формуле:

 

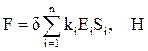, (35)

 

где d – коэффициент допустимого продольного растяжения конструкции кабеля;

k_i – коэффициент, учитывающий расположение i-гo элемента относи­тельно оси конструкции кабеля;

E_i – модуль продольной упругости материала i-гo элемента конструк­ции кабеля, Па;

S_i – поперечное сечение i-го элемента конструкции кабеля, м².

 

Коэффициент, учитывающий расположение элементов конструкций ка́беля, имеет следующие значения:

• k_i = 1 для элементов, параллельных оси кабеля (испытывающих ме­ханическое напряжение);

• k_i = 0 для элементов, не испытывающих механическое напряжение (обычно оптических волокон);

• k_i = cosy_i для элементов, испытывающих напряжения и расположен­ных по спирали с углом подъема y₁ (обычно для оптических моду­лей можно считать угол подъема 30 – 35°).

 

Таблица 7. Значения некоторых параметров элементов конструкций ОК.

Материал	Плотность, г/см3	Сопротивление разрыву, МПа	Модуль упругости, ГПа	Относительное удли­нение при разрыве, %	ТКЛР, 1/К
Сталь	7,86			2,0	6,6*10 - 6
Медь	8,7 – 8,9
Алюминий	2,7
Кварцевое волокно	2,48			5,4	3,1*10 - 6
Полиэтилен	0,92 – 0,93		0,15 – 0,25
Полибутилентерефталат	1,31		1,6		1,5*10 - 4
Полиамид	1,06		1,7		7,8*10 - 5
Поликарбонат	1,2		2,3		6,5*10 - 5
Фторопласт	2,1 - 2,3		2,25
Полистирол	1,05		1,2 – 1,5
ПВХ	1,3 – 1,7
Нейлон	1,14		6 - 13
Тварон	1,45			2,65	– 3*10 - 6
Кевларовая нить	1,44	2950 – 3070	72 – 114	2,5 – 3,6	– 2*1 0 - 6
СВМ	1,25
Высокопрочное полиэтиленовое волокно	0,98			3...4	-

 

Коэффициент допустимого продольного растяжения d для разных типов конструкций ОК меняется в пределах 0,01 – 0,025.

В случае продольного армирования кабеля одной центральной жи­лой из высокопрочного материала, ее сечение может быть определено из выражения:

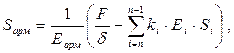(36)

где d – коэффициент допустимого продольного растяжения конструкции кабеля;

k_i – коэффициент, учитывающий расположение i-го элемента относи­тельно оси конструкции кабеля;

Е_i – модуль продольной упругости материала i-го элемента конструк­ции кабеля;

S_i – поперечное сечение i-гo элемента конструкции кабеля, м².

Длину регенерационного участка ограничивает один из двух фак­торов: затухание или дисперсия. При определении длины регенерационного участка необходимо на первом этапе найти максимально до­пустимое расстояние (ограниченное затуханием световодного тракта), на которое можно передать сигнал, а затем его восстановить. Вторым этапом определяют пропускную способность оптического кабеля и на­ходят длину трассы, на которую ещё возможно передавать оптические сигналы с заданной скоростью. В многомодовых ОВ длина регенерационного участка обычно лимитируется дисперсией, а в одномодовых ОВ лимитируется затуханием.

При определении длины регенерационного участка, лимитирован­ного затуханием, следует пользоваться выражением:

(37)

где Э – энергетический потенциал системы передачи;

С – энергетический запас системы;

a_пас – дополнительные потери в пассивных компонентах ВОЛС (на вводе-выводе), дБ;

a_каб – коэффициент затухания оптического кабеля, дБ/км;

a_соед – потери в неразъемном соединении, дБ;

L_стр – строительная длина кабеля, км.

Энергетический потенциал системы передачи (Э) определяет мак­симально допустимое затухание оптического сигнала в оптическом ка­беле, в разъемных и неразъемных соединениях на участке регенера­ции, а также другие потери в узлах аппаратуры. Энергетический по­тенциал определяется как разность между уровнем мощности опти­ческого сигнала, введённого в волокно, и уровнем мощности на входе приемного устройства, при котором коэффициент ошибок регенерато­ра не превышает заданного значения, установленного для данной сис­темы передачи. Энергетический потенциал зависит от ско­рости передачи, технического уровня элементов электрооптических и оптоэлектронных преобразователей, длины волны используемого ис­точника излучения и других факторов и задаётся для каждого вида ап­паратуры ВОСП. В таблице 8 приведены справочные данные энергети­ческого потенциала различных отечественных систем.

 

Таблица 8. Справочные данные различных отечественных систем ВОЛС.

Система	Длина волны, мкм	Скорость передачи, Мбит/с	Число каналов	Энергетический потенциал, дБ
Соната-2	0,85	8,448
ИКМ -120-4/5	0,85 (ЛД)	8,448
ИКМ -120-4/5	0,85 (СИД)	8,448
ИКМ -120-4/5	1,3 (ЛД)	8,448
ИКМ-120-4/5	1,3 (СИД)	8,448
ИКМ -480-5	1,3	34,368
Сопка-Г	1,3	34,368
Сопка-Г	1,3	8,448
Сопка -3	1,3	34,368
Сопка -3М	1,55	34,368
Сопка-4	1,55	139,264
Сопка-4М	1,3	139,264
Сопка-5	1,55	668,4672

 

Энергетический запас системы (С) обычно составляет 3 – 6 дБ, он не­обходим для компенсации эффекта старения элементов аппаратуры и оптического ка́беля, компенсации дополнительных потерь при ремон­те оптического кабеля (потери на стыках кабельных вставок) и других отклонений параметров участка в процессе эксплуатации.

Дополнительные потери в пассивных компонентах ВОЛС (А_а) со­ставляют 3–5 дБ и возникают за счет разъемных соедините­лей, устройств соединения линейного кабеля со станционным и т. д.

Ограничение длины регенерационного участка дисперсией. Длина регенерационного участка ограничивается также пропуск­ной способностью оптического кабеля. Пропускная способность DF является одним из основных параметров ВОЛС, так как она определя­ет полосу частот, пропускаемую оптическим волокном, и соответ­ственно объем информации, который можно передать по оптическому кабелю на длину регенерационного участка. Пропускная способность оптического кабеля существенно зависит от используемых в них типов оптических волокон (одномодовые, многомодовые ступенчатые, гра­диентные), которые могут иметь различные дисперсионные парамет­ры.

Связь между величиной уширения импульсов и полосой частот выражается соотношением:

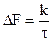; (38)

где k – коэффициент, учитывающий форму оптического импульса (от 0,44 при гауссовой форме импульса до 0,6 при прямоугольных импульсах); t – уширение импульса.

 

Дисперсионные искажения существенно зависят от длины опти­ческого волокна, поэтому DF нормируется на один кило­метр оптического кабеля. Так, если на километровой длине оптиче­ского волокна происходит уширение импульса на t =10 нc, то его пропускная способность DF ограничена 44 МГц (при гауссовой форме импульса).

Для того, чтобы оценить способность какого-либо участка ВОЛС (L_x) передавать информацию с определенной шириной полосы частот, при известной нормированной полосе пропускания ОК на один километр (DF₁), для коротких линий, меньших, чем длина установившегося режима (L_x <L_c), следует использовать выражение:

(при L_x < L_c). (39)

Для линий, больших, чем длина установившегося режима (L_x > L_c), следует использовать выражение:

(при L_x > L_c). (40)

Длина установившегося режима передачи для ступенчатого многомодового волокна составляет 5 – 7 км, для градиентного волокна 10 – 15 км. Для одномодовых волокон, в которых распространяется один тип волны, следует считать L_с = 25 – 30 км. Для одномодовых волокон L_c является длиной установившегося режима (либо длиной модовой связи) ортого­нально-поляризованных двух мод (направляемая мода представляется двумя ортогонально-поляризованными модами одного типа).

Если известно не нормированное значение полосы пропускания ОК на один километр, а известна пропускная способность DF оптического кабеля длиной L, то можно воспользоваться выражениями:

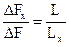для коротких линий, у которых L_x<L_c; (41)

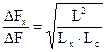для длинных линий, у которых L_x > L_c. (42)

 

Как видно из выражений, с увеличением длины линии уменьшается пропускная способность световода DF.

На рис. 4 показана зависи­мость дисперсии и пропускной способности от длины линии.

 

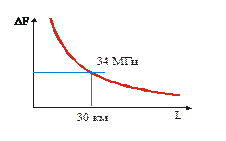
Рис. 4. Рис. 5.

 

Для определения длины регенерационного участка, исходя из фор­мул (35) и (36), строят график изменения DF_x от длины трассы ВОЛС L_x. На основании этого графика для требуемой системы пере­дачи определяют длину регенерационного участка. Скорость передачи системы соответствует необходимой ширине полосы про­пускания регенерационного участка.

На рисунке 5 показан пример опре­деления длины регенерационного участка третичной цифровой системы.

После нахождения длины регенерационного участка, лимитиро­ванного дисперсией, проводят её сравнение с найденной ранее длиной регенерационного участка, лимитированного затуханием, и выбирают наименьшее значение.

 

 

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: