 |
Давление жидкости на вертикальную пластинку.
|
|
|
|
Применение определенного интеграла в физике
Работа переменной силы.
Определенный интеграл широко применяется при решении различных физических задач. С помощью определенного интеграла можно вычислять: путь, пройденный материальной точкой, если известна скорость движения; работу переменной силы; силу давления жидкости на плоскую фигуру; статические моменты и координаты центра масс плоской кривой и плоской фигуры; вычислить кинетическую и потенциальную энергию тела в поле сил и т.д.
Пусть материальная точка М перемещается вдоль оси Ох под действием переменной силы F=F(х), направленной параллельно этой оси. Работа, произведенная силой при перемещении точки М из положения х = а в положение х = b (а <bЬ), находится по формуле: A = 
Пример 1. Какую работу нужно затратить, чтобы растянуть пружину на 0,05 м, если сила 100 Н растягивает пружину на 0,01 м?
Решение: По закону Гука упругая сила, растягивающая пружину, пропорциональна этому растяжению х, т. е. F = kх, где k— коэффициент пропорциональности. Согласно условию задачи, сила F = 100 Н растягивает пружину на х = 0,01 м; следовательно, 100 = k 0,01, откуда k = 10000; следовательно, F =10000 х.
Искомая работа на основании формулы A =  равна
равна
A = 
Пример 2. Найти работу, которую необходимо затратить, чтобы выкачать через край жидкость из вертикального цилиндрического резервуара высоты Н м и радиусом основания Rм (рис. 13).
| Рис.13 |
 Решение: Работа, затрачиваемая на поднятие тела весом р на высоту h, равна р • Н. Но различные слои жидкости в резервуаре находятся на различных глубинах и высота поднятия (до края резервуара) различных слоев не одинакова.
Решение: Работа, затрачиваемая на поднятие тела весом р на высоту h, равна р • Н. Но различные слои жидкости в резервуаре находятся на различных глубинах и высота поднятия (до края резервуара) различных слоев не одинакова.
Для решения поставленной задачи применим схему II (метод дифференциала). Введем систему координат.
|
|
|
1.Работа, затрачиваемая на выкачивание из резервуара слоя жидкости толщиной х (0 ≤ х ≤ Н), есть функция от х, т. Е. А = А(х),
где (0 ≤ х ≤ Н)(A(0) = 0, A (H) = А0).
2. Находим главную часть приращения ΔA при изменении х на величину Δх = dx, т. Е. находим дифференциал d А функции А(х).
Ввиду малости dх считаем, что “элементарный” слой жидкости находится на одной глубине х (от края резервуара). Тогда d А = dрх, где d р- вес этого слоя; он равен g  АV, где g- ускорение свободногопадения,
АV, где g- ускорение свободногопадения,  -плотность жидкости, dv - объем “элементарного” слоя жидкости (на рисунке он выделен), т. Е. d р = g
-плотность жидкости, dv - объем “элементарного” слоя жидкости (на рисунке он выделен), т. Е. d р = g  . Объем указанного слоя жидкости, очевидно, равен
. Объем указанного слоя жидкости, очевидно, равен  , где dx-высота цилиндра (слоя),
, где dx-высота цилиндра (слоя),  -площадь его основания, т. Е. dv=
-площадь его основания, т. Е. dv= 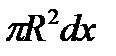 .
.
Таким образом, d р =  . И
. И 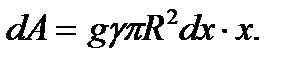
3) Интегрируя полученное равенство в пределах от х = 0 до х = Н, находим
A 
Путь, пройденный телом.
Пример 3. Пусть материальная точка перемещается по прямой с переменной скоростью v =v(t). Найдем путь S, пройденный ею за промежуток времени от t  до t2.
до t2.
Решение: Из физического смысла производной известно, что при движении точки в одном направлении “скорость прямолинейного движения
равна производной от пути по времени”, т. Е. v(t) =  . Отсюда следует, что dS = v(t)dt. Интегрируя полученное равенство в пределах от t
. Отсюда следует, что dS = v(t)dt. Интегрируя полученное равенство в пределах от t  до t
до t  ,
,
получаем S = 
Пример 4. Найти путь, пройденный телом за 4 секунды от начала движения, если скорость тела v(t) = 10t + 2 (м/с).
Решение: Если v(t) = 10t + 2 (м/с), то путь, пройденный телом от начала движения (t = 0) до конца 4-й секунды, равен
S = 
Давление жидкости на вертикальную пластинку.
По закону Паскаля давление жидкости на горизонтальную пластину равно весу столба этой жидкости, имеющего основанием пластинку, а высотой — глубину ее погружения от свободной поверхности жидкости, т. Е. Р = g  , где g — ускорение свободного падения,
, где g — ускорение свободного падения,  — плотность жидкости, S — площадь пластинки, h — глубина ее погружения.
— плотность жидкости, S — площадь пластинки, h — глубина ее погружения.
|
|
|

| Рис. 14 |
Пусть в жидкость погружена вертикально пластина, ограниченная линиями х = а, х = b, y  и y
и y  . Для нахождения давления Р жидкости на эту пластину применим схему II (метод дифференциала).
. Для нахождения давления Р жидкости на эту пластину применим схему II (метод дифференциала).
1. Пусть часть искомой величины Р есть функция от х: р = р(х), т. Е. р = р(х) — давление на часть пластины, соответствующее отрезку [а; b]значений переменной х, где х  [a; b] (р(a) = 0, р(b) = Р).
[a; b] (р(a) = 0, р(b) = Р).
| Рис 14 |
Тогда по закону Паскаля dр = 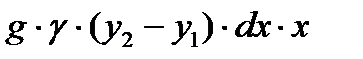 .
.
3. Интегрируя полученное равенство в пределах от х = а до х = b, получим
P =  или P =
или P = 
| Рис. 15 |
 Пример 5. Определить величину давления воды на полукруг, вертикально погруженный в жидкость, если его радиус R, а центр О находится на свободной поверхности воды (рис. 15).
Пример 5. Определить величину давления воды на полукруг, вертикально погруженный в жидкость, если его радиус R, а центр О находится на свободной поверхности воды (рис. 15).
Решение: Воспользуемся полученной формулой для нахождения давления жидкости на вертикальную пластинку. В данном случае пластинка ограничена линиями у 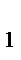 = -
= -  , y
, y  , x = 0, x = R.
, x = 0, x = R.
P = 
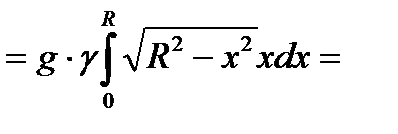


|
|
|


