 |
Расчетно-графическая работа №1
|
|
|
|
Министерство общего и профессионального образования РФ
Владимирский государственный университет
Кафедра общей и прикладной физики
Расчетно-графическая работа №1
№ 102
Материальная точка движется прямолинейно с ускорением a=5 м/с2. Определить, на сколько путь, пройденный точкой в n-ю секунду, будет больше пути, пройденного в предыдущую секунду. Принять v0=0.
Дано:

 1. Путь при равноускоренном движении без
1. Путь при равноускоренном движении без
 начальной скорости подсчитываем по формуле:
начальной скорости подсчитываем по формуле:

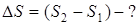

Пусть  тогда путь за n секунду:
тогда путь за n секунду:

- за (n-1) секунд:

- за (n-2) секунд:

2. Путь за одну (n-1)-ю секунду:

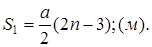
Путь же за одну n-ю секунду будет равен:


Искомая разность путей:



Разность путей численно равна ускорению материальной точки.
№ 112
С тележки свободно движущейся по горизонтальному пути со скоростью v1=3 м/с, в сторону, противоположную движению тележки, прыгает человек, после чего скорость тележки изменилась и стала равной u1=4 м/с. Определить горизонтальную составляющую скорости u2X человека при прыжке относительно тележки. Масса тележки m1=210 кг, масса человека m2=70 кг.
Дано:


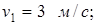





Система («Человек-тележка») замкнута (изолированная). Применим закон сохранения импульса:

то есть:

или на ось Х:

найдем U2X:

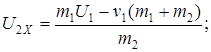
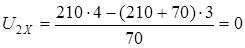
Ответ: U2x=0.
№ 122
По небольшому куску мягкого железа, лежащему на наковальне массой m1=300 кг, ударяет молот массой m2=8 кг. Определить КПД h удара, если удар неупругий. Полезной считать энергию, затраченную на деформацию куска железа.
|
|
|
Дано:

 Перед ударом скорость молота была v, то кинетичес-
Перед ударом скорость молота была v, то кинетичес-
 кая энергия молота, представляющая собой полную
кая энергия молота, представляющая собой полную
 механическую энергию будет:
механическую энергию будет:

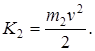
 Ввиду не упругости удара (остановка молота) эта энергия является затраченной энергией:
Ввиду не упругости удара (остановка молота) эта энергия является затраченной энергией:
 или
или 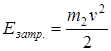
Будем считать систему (молот-наковальня с куском мягкого железа) изолированной и применим закон сохранения импульса:
 т.е.
т.е.
 (отскакивает молот).
(отскакивает молот).
Скорость наковальни с железом:
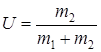 и следовательно кинетическая энергия наковальни с молотом:
и следовательно кинетическая энергия наковальни с молотом:

Имеем согласно закону сохранения энергии:
 т. е.
т. е.
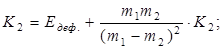

Eдеф.- энергия, которая пошла на деформацию куска железа, откуда

 то
то 
По определению коэффициента полезного действия:

Ответ: h=97,47%
№ 132
Из шахты глубиной h=600 м поднимают клеть массой m1=3,0 т на канате, каждый метр которого имеет массу m=1,5 кг. Какая работа А совершается при поднятии клети на поверхность Земли? Каков КПД h подъемного устройства?
Дано:

 1. Работа по подъему клети (без троса), т.е. полезная
1. Работа по подъему клети (без троса), т.е. полезная
 работа:
работа:



2. Работа по подъему троса:  - длина;
- длина;

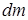 - масса;
- масса;
 - сила тяжести;
- сила тяжести;
 Выделим их:
Выделим их:
 - элементарная работа по равномерному
- элементарная работа по равномерному
подъему (внешняя сила  равна силе тяжести
равна силе тяжести
 элемента троса на высоту
элемента троса на высоту 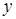 будет равна:
будет равна:

где 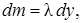 где
где 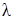 - плотность троса (линейная),
- плотность троса (линейная),
она задана.

Интегрируем:


3. Вся затраченная работа (общая работа по подъему клети с тросом):



4. КПД подъемного устройства:

 т.е.
т.е. 
Ответ: 

№ 142
По касательной к шкифу маховика в виде диска диаметром D=75 см и массой m=40 кг приложена сила F=1 кН. Определить угловое ускорение e и частоту вращения n маховика через время t=10 с после начала действия силы, если радиус r шкифа равен 12 см. Силой трения пренебречь.
|
|
|
Дано:






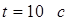


1. По второму закону Ньютона:

 где
где  - сила инерции маховика диска.
- сила инерции маховика диска.

 .
.

2. При равномерном вращении:

Разгон маховика начался из состояния покоя,  . Получаем:
. Получаем:
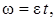
где  связана с частотой вращения
связана с частотой вращения
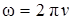 ,
,
 получаем:
получаем:

Ответ: 
 .
.
№ 152
На скамье Жуковского стоит человек и держит в руках стержень вертикально по оси скамьи. Скамья с человеком вращается с угловой скоростью w1=4 рад/с. С какой угловой скоростью w2 будет вращаться скамья с человеком, если повернуть стержень так, чтобы он занял горизонтальное положение? Суммарный момент инерции человека и скамьи I=5 кг×м2. Длина стержня l=1,8 м, масса m=6 кг. Считать, что центр масс стержня с человеком находится на оси платформы.
Дано:

 1. Закон сохранения момента импульса твердого
1. Закон сохранения момента импульса твердого
 тела будет иметь вид:
тела будет иметь вид:

 , откуда
, откуда
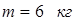
 , (1)
, (1)

где  и
и

 (2)
(2)
3. Вычисляем момент инерции стержня относительно вертикальной оси, которая проходит через середину стержня:


Элементарная масса 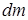 принята за материальную точку, для нее:
принята за материальную точку, для нее:
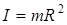 , где
, где 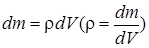 и где
и где
 (S-поперечное сечение стержня)
(S-поперечное сечение стержня)
 .
.
Таким образом:
 .
.
Интегрируя, получаем:

( - плотность материала стержня)
- плотность материала стержня)
Выразим ее:

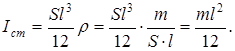
Подставим в (2):

Подставим в (1):

Ответ: 
№ 162
Какая работа А будет совершена силами гравитационного поля при падении на Землю тела массой m=2 кг: 1) с высоты h=1000 км; 2) из бесконечности?

Дано:





 Эл. Работа гравитац. силы на отрезке пути
Эл. Работа гравитац. силы на отрезке пути 

 где
где

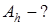
 т.е.
т.е.
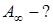

откуда интегрированием получаем:
|
|
|
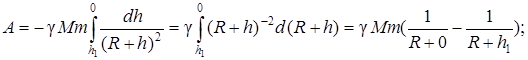
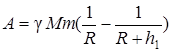
При 
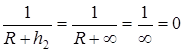


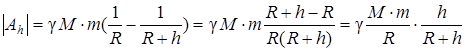

Ответ: 

№ 172
Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых x=A1sinw1t и y=A2cosw2t, где А1=8 см,
А2=4 см, w1=w2=2 с-1. Написать уравнение траектории и построить ее. Показать направление движения точки.
Дано:


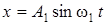 1.
1.  (1)
(1)
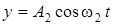
 (2)
(2)





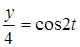


Возведем в квадрат:

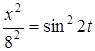

Сложим почленно:
 - траекторией точки является эллипс с полуосями: а=8, в=4
- траекторией точки является эллипс с полуосями: а=8, в=4
 |
2. Установим направление движения координаты точек в момент времени  и, например,
и, например, 
По уравнениям (1) и (2):





 Þ по часовой стрелке.
Þ по часовой стрелке.
|
|
|


