 |
Определение кривой второго порядка
|
|
|
|
Пример.
В обобщенной полярной системе координат построить кривую  .
.
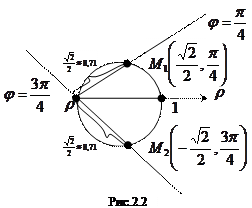 Для решения задачи следует найти точки, лежащие на кривой, давая
Для решения задачи следует найти точки, лежащие на кривой, давая 
 значения через какой-то промежуток (чем меньше промежуток, тем точнее можно построить кривую, но тем больше объем вычислительной работы). Результат построения – окружность с диаметром
значения через какой-то промежуток (чем меньше промежуток, тем точнее можно построить кривую, но тем больше объем вычислительной работы). Результат построения – окружность с диаметром  – приведен на рис. 2.2. Там же показаны две точки,
– приведен на рис. 2.2. Там же показаны две точки,  и
и  , принадлежащие этой окружности, способ построения которых ясен из рисунка. Любые другие точки этой кривой строятся аналогично.
, принадлежащие этой окружности, способ построения которых ясен из рисунка. Любые другие точки этой кривой строятся аналогично.
Всякой линии на плоскости  , рассматриваемой как множество точек, соответствует некоторое уравнение, в которое входят координаты любой точки
, рассматриваемой как множество точек, соответствует некоторое уравнение, в которое входят координаты любой точки  ("текущей точки"), лежащей на этой линии. Такое уравнение называется уравнением данной линии.
("текущей точки"), лежащей на этой линии. Такое уравнение называется уравнением данной линии.
Чтобы составить уравнение линии как геометрического места точек, обладающих одинаковым свойством, нужно:
1) взять произвольную (текущую) точку 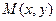 линии,
линии,
2) записать равенством общее свойство всех точек  линии,
линии,
3) входящие в это равенство отрезки (и углы) выразить через текущие координаты точки 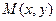 и через данные в задаче.
и через данные в задаче.
Пример. В декартовой прямоугольной системе координат вывести уравнение геометрического места точек, сумма квадратов расстояний которых до двух данных точек  и
и 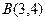 есть величина постоянная, равная 47.
есть величина постоянная, равная 47.
Решение.
Обозначим буквой  произвольную точку линии.
произвольную точку линии.
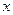 и
и 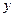 - текущие координаты этой точки.
- текущие координаты этой точки.
Запишем геометрическое свойство линии символически.
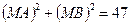 . (1)
. (1)
Выразим 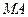 и
и  через текущие координаты точки
через текущие координаты точки  :
:
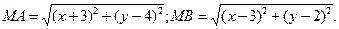
Подставив полученные выражения в равенство (1), найдем уравнение, связывающее координаты  точки
точки  :
:

Упростим последнее уравнение:
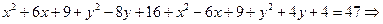

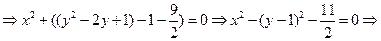

Получили уравнение окружности с центром в т. (0,1) и радиусом 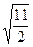 .
.
|
|
|
ПРЯМАЯ НА ПЛОСКОСТИ
Прямая на плоскости в декартовой прямоугольной системе координат  может быть задана уравнением одного из следующих видов:
может быть задана уравнением одного из следующих видов:
1) 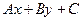 - общее уравнение прямой.
- общее уравнение прямой.
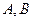 - координаты нормального вектора
- координаты нормального вектора 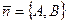 прямой (вектора, перпендикулярного данной прямой).
прямой (вектора, перпендикулярного данной прямой).
2)  - уравнение прямой, проходящей через точку
- уравнение прямой, проходящей через точку 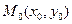 перпендикулярно вектору
перпендикулярно вектору  .
.
3) 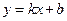 - уравнение с угловым коэффициентом, где
- уравнение с угловым коэффициентом, где 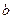 - отрезок, отсекаемый прямой на оси
- отрезок, отсекаемый прямой на оси 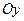 ,
, 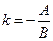 или
или 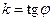 , где
, где  - угол наклона прямой к оси
- угол наклона прямой к оси 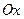 .
.
4) 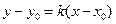 - уравнение прямой с угловым коэффициентом
- уравнение прямой с угловым коэффициентом  , проходящей через данную т.
, проходящей через данную т. 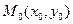 .
.
5) 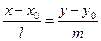 - каноническое уравнение прямой, или уравнение прямой, проходящей через т.
- каноническое уравнение прямой, или уравнение прямой, проходящей через т. 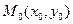 параллельно направляющему вектору
параллельно направляющему вектору  .
.
6)  - параметрические уравнения прямой,
- параметрические уравнения прямой, 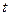 - параметр.
- параметр.
7) 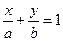 - уравнение прямой в отрезках, где
- уравнение прямой в отрезках, где  и
и 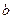 - величины отрезков, отсекаемых прямой на координатных осях
- величины отрезков, отсекаемых прямой на координатных осях 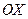 и
и 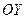 соответственно.
соответственно.
8)  - уравнение прямой, проходящей через две данные точки
- уравнение прямой, проходящей через две данные точки 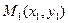 и
и 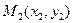 .
.
Угол между двумя прямыми можно найти, зная угловые коэффициенты прямых: 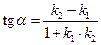 .
.
Условие параллельности двух прямых: 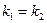 или
или  .
.
Условие перпендикулярности двух прямых:  , или
, или 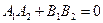 .
.
плоскость
Плоскость 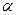 в декартовой прямоугольной системе координат
в декартовой прямоугольной системе координат 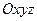 может быть задана уравнением одного из следующих видов:
может быть задана уравнением одного из следующих видов:
1) 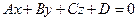 - общее уравнение плоскости,
- общее уравнение плоскости, 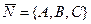 - нормальный вектор плоскости,
- нормальный вектор плоскости, 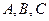 - его координаты;
- его координаты;
2)  - уравнение плоскости, проходящей через т.
- уравнение плоскости, проходящей через т. 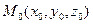 перпендикулярно нормальному вектору
перпендикулярно нормальному вектору 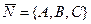 .
.
3) 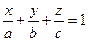 - уравнение плоскости в отрезках, где
- уравнение плоскости в отрезках, где  - отрезки, отсекаемые плоскостью на осях координат
- отрезки, отсекаемые плоскостью на осях координат 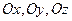 соответственно.
соответственно.
4)  - уравнение плоскости, проходящей через три данные точки:
- уравнение плоскости, проходящей через три данные точки: 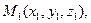
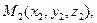
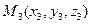 .
.
ПРЯМАЯ В ПРОСТРАНСТВЕ
Прямая в пространстве может быть задана:
1) общими уравнениями:
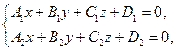
т.е. системой уравнений двух пересекающихся плоскостей.
2) параметрическими уравнениями:
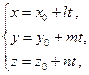
где 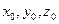 - координаты данной точки, а
- координаты данной точки, а 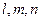 – координаты направляющего вектора прямой
– координаты направляющего вектора прямой 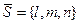 , т.е. вектора, параллельного данной прямой;
, т.е. вектора, параллельного данной прямой;
3) каноническими уравнениями:
|
|
|

4) уравнениями прямой, проходящей через две точки:
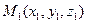 и
и 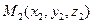 :
:
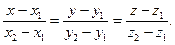
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПЛОСКОСТЕЙ
И ПРЯМЫХ В ПРОСТРАНСТВЕ
Угол  между плоскостями
между плоскостями 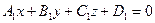 и
и  определяется по формуле
определяется по формуле
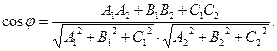
Условие перпендикулярности плоскостей:
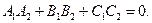
Условие параллельности плоскостей: 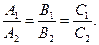
Расстояние от точки 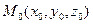 до плоскости, определяемой уравнением
до плоскости, определяемой уравнением 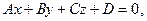 можно найти по формуле
можно найти по формуле
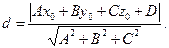
Угол между двумя прямыми в пространстве, заданными их каноническими уравнениями, определяется по формуле
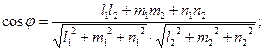
условие параллельности двух прямых: 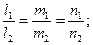 условие перпендикулярности двух прямых:
условие перпендикулярности двух прямых:  Угол между прямой и плоскостью определяется по формуле
Угол между прямой и плоскостью определяется по формуле
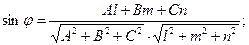
условие параллельности прямой и плоскости: 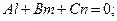
условие перпендикулярности прямой и плоскости: 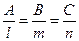 .
.
При решении задач надо уметь переходить от общих уравнений прямой в пространстве к каноническим.
Пример.
По уравнениям плоскостей 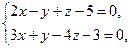
образующих прямую, составить ее уравнения в каноническом виде. Решение. Определим координаты одной точки прямой: положим  , тогда для значений
, тогда для значений  и
и 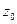 решим систему уравнений
решим систему уравнений 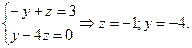
Теперь канонические уравнения имеют вид
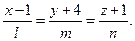
Направляющий вектор 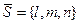 искомой прямой будет перпендикулярен нормальным векторам
искомой прямой будет перпендикулярен нормальным векторам 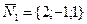 и
и 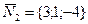 данных плоскостей, следовательно, его координаты можно найти, используя векторное произведение.
данных плоскостей, следовательно, его координаты можно найти, используя векторное произведение.
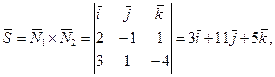 т.е.
т.е. 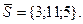
Канонические уравнения искомой прямой имеют вид

КРИВЫЕ ВТОРОГО ПОРЯДКА
Определение кривой второго порядка
Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих декартовых координат.
В общем случае это уравнение имеет следующий вид:
 (1)
(1)
где коэффициенты 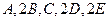 и
и 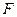 — действительные числа и, кроме того, по крайней мере одно из чисел:
— действительные числа и, кроме того, по крайней мере одно из чисел:  или
или  отлично
отлично
от нуля. Коэффициенты при 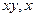 и
и 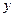 обозначены соответственно через
обозначены соответственно через  и
и 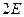 для удобства преобразований уравнения. Известно, что уравнение окружности с центром в точке
для удобства преобразований уравнения. Известно, что уравнение окружности с центром в точке 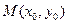 и радиуса
и радиуса 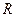 имеет вид
имеет вид
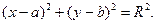 (2)
(2)
Это уравнение второй степени относительно 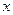 и
и 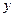 . Следовательно,
. Следовательно,
окружность есть кривая второго порядка. Далее будут рассмотрены четыре кривые второго порядка: окружность, эллипс, гипербола и парабола.
Окружность
Раскрыв скобки в уравнении (2) и выполнив некоторые тождественные преобразования, мы получим уравнение окружности в следующем виде:
|
|
|

При сравнении этого уравнения с общим уравнением (1) кривой второго порядка легко заметить, что для уравнения окружности выполнены два условия: 1) отсутствует член с произведением координат 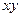 ; 2) коэффициенты при
; 2) коэффициенты при  и
и 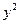 равны между собой.
равны между собой.
Пример. Показать, что уравнение 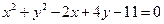 определяет окружность, и найти координаты ее центра и радиус.
определяет окружность, и найти координаты ее центра и радиус.
Решение. Условия 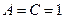 и
и 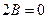 здесь выполняются. Преобразуем данное уравнение:
здесь выполняются. Преобразуем данное уравнение:
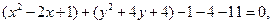
или

Мы получили уравнение окружности с центром 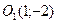 и радиусом
и радиусом 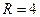 .
.
Пример. Показать, что уравнение  не определяет никакой линии.
не определяет никакой линии.
Решение. Преобразуем это уравнение:
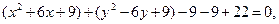
или
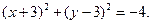
Теперь ясно, что данное уравнение не определяет никакой линии.
Эллипс
Определение. Эллипсом называется геометрическое место точек плоскости, сумма расстояний каждой из которых от двух данных точек этой плоскости, называемых фокусами, есть постоянная величина (при условии, что эта величина больше расстояния между фокусами).
 Обозначим фокусы через
Обозначим фокусы через 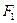 и
и  , расстояние между ними – через
, расстояние между ними – через 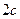 , а постоянную величину, равную сумме расстояний от каждой точки эллипса до фокусов, – через
, а постоянную величину, равную сумме расстояний от каждой точки эллипса до фокусов, – через 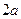 (по условию
(по условию 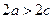 ).
).
Построим декартову систему координат так, чтобы фокусы 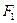 и
и  оказались на оси абсцисс, а начало координат совпало с серединой отрезка
оказались на оси абсцисс, а начало координат совпало с серединой отрезка  (рис.2.3). Тогда фокусы будут иметь следующие координаты: левый фокус
(рис.2.3). Тогда фокусы будут иметь следующие координаты: левый фокус 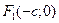 и правый фокус
и правый фокус 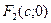 . Выведем уравнение эллипса в выбранной нами системе координат. С этой целью рассмотрим произвольную точку
. Выведем уравнение эллипса в выбранной нами системе координат. С этой целью рассмотрим произвольную точку 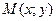 эллипса. По определению эллипса сумма расстояний от этой точки до фокусов
эллипса. По определению эллипса сумма расстояний от этой точки до фокусов 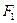 и
и  равна
равна 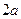 :
:
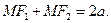
Пользуясь формулой для расстояния между двумя точками, получим 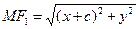 ,
, 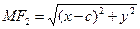 ; следовательно,
; следовательно,

Для упрощения этого уравнения запишем его в форме

Возведя затем обе части уравнения в квадрат, получим

или, после очевидных упрощений:
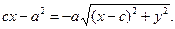
Теперь опять возводим обе части уравнения в квадрат, после чего будем иметь
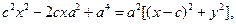
или после тождественных преобразований:
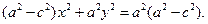
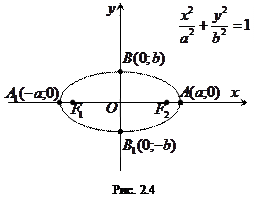 Так как согласно условию в определении эллипса
Так как согласно условию в определении эллипса 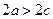 , то
, то 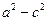 — число положительное. Введем обозначение
— число положительное. Введем обозначение
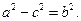
Тогда уравнение примет следующий вид:
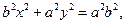
или
|
|
|
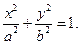
Можно показать, что эллипс имеет форму, изображенную на рис. 2.4. Точки пересечения эллипса с осями называются вершинами эллипса. Из симметрии эллипса следует, что, кроме вершин  и
и 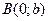 , эллипс имеет еще две вершины:
, эллипс имеет еще две вершины: 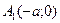 и
и  (см. рис. 2.4). Отрезки
(см. рис. 2.4). Отрезки 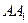 и
и 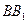 , соединяющие противоположные вершины эллипса, а также их длины
, соединяющие противоположные вершины эллипса, а также их длины 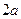 и
и 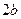 , называются соответственно большой и малой осями эллипса. Числа
, называются соответственно большой и малой осями эллипса. Числа  и
и 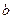 называются соответственно большой и малой полуосями эллипса.
называются соответственно большой и малой полуосями эллипса.
Отношение 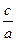 половины расстояния между фокусами к большой полуоси эллипса называется эксцентриситетом эллипса и обозначается обычно буквой
половины расстояния между фокусами к большой полуоси эллипса называется эксцентриситетом эллипса и обозначается обычно буквой 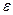 :
:
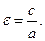
Так как  , то эксцентриситет эллипса меньше единицы:
, то эксцентриситет эллипса меньше единицы: 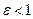 .
.
Пример. Найти каноническое уравнение эллипса, зная его большую полуось 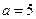 и эксцентриситет
и эксцентриситет 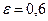 .
.
Решение. По условию 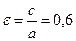 . Следовательно, половина расстояния между фокусами
. Следовательно, половина расстояния между фокусами  . Но тогда квадрат малой полуоси эллипса
. Но тогда квадрат малой полуоси эллипса  . Таким образом, искомое каноническое уравнение эллипса имеет следующий вид:
. Таким образом, искомое каноническое уравнение эллипса имеет следующий вид:
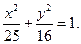
Пример. Составить каноническое уравнение эллипса, проходящего через точку 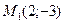 и имеющего большую полуось
и имеющего большую полуось 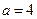 .
.
Решение. Каноническое уравнение эллипса при 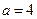 имеет следующий вид:
имеет следующий вид:
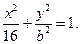
Этому уравнению должны удовлетворять координаты точки 
Следовательно,
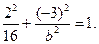
Найдя отсюда 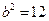 и подставив его в уравнение, получим искомое каноническое уравнение эллипса:
и подставив его в уравнение, получим искомое каноническое уравнение эллипса:
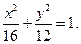
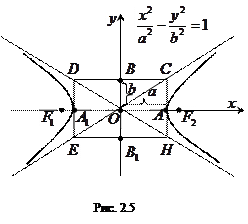
Гипербола
Определение. Гиперболой называется геометрическое место точек плоскости, абсолютная величина разности расстояний каждой из которых от двух данных точек этой плоскости; называемых фокусами, есть постоянная величина, при условии, что эта величина не равна нулю и меньше расстояния между фокусами.
Обозначим расстояние между фокусами 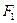 и
и  через
через 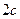 , а постоянную величину, равную модулю разности расстояний от каждой точки гиперболы до фокусов, через
, а постоянную величину, равную модулю разности расстояний от каждой точки гиперболы до фокусов, через 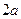 (по условию
(по условию  ). Как и в случае эллипса, ось абсцисс проведем через фокусы, а за начало координат примем середину отрезка
). Как и в случае эллипса, ось абсцисс проведем через фокусы, а за начало координат примем середину отрезка 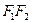 (см. рис. 2.3). Фокусы в такой системе будут иметь координаты
(см. рис. 2.3). Фокусы в такой системе будут иметь координаты 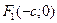 и
и  . Выведем уравнение гиперболы в выбранной системе координат. По определению гиперболы для любой ее точки
. Выведем уравнение гиперболы в выбранной системе координат. По определению гиперболы для любой ее точки 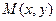 имеем
имеем 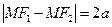 , или
, или

Но 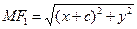 и
и  Поэтому получим
Поэтому получим

После упрощений, подобных тем, которые были сделаны при выводе уравнения эллипса, получим следующее уравнение:

 Нетрудно заметить, что это уравнение совпадает с уравнением, полученным для эллипса. Однако здесь разность
Нетрудно заметить, что это уравнение совпадает с уравнением, полученным для эллипса. Однако здесь разность  , так как для гиперболы
, так как для гиперболы 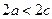 . Поэтому положим
. Поэтому положим
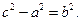
Тогда последнее уравнение приводится к следующему виду:
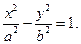
Форма гиперболы и способ её построения показаны на рис. 2.5. Точки  и
и  – вершины гиперболы. Прямые
– вершины гиперболы. Прямые  и
и  , имеющие уравнения
, имеющие уравнения  , называются асимптотами гиперболы.
, называются асимптотами гиперболы.
Отношение половины расстояния между фокусами к действительной полуоси гиперболы называется эксцентриситетом гиперболы и обозначается обычно буквой 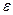 :
:
|
|
|
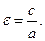
Так как для гиперболы 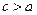 , то эксцентриситет гиперболы больше единицы
, то эксцентриситет гиперболы больше единицы 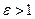 .
.
Пример. Составить каноническое уравнение гиперболы, зная что расстояние между ее фокусами равно 26, а эксцентриситет равен 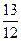 .
.
Решение. По условию  и
и 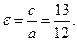 Следовательно, большая полуось гиперболы
Следовательно, большая полуось гиперболы 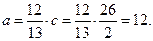 Согласно формуле малая полуось гиперболы
Согласно формуле малая полуось гиперболы 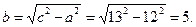
Уравнение гиперболы имеет следующий вид:

Пример. Гипербола, оси которой совпадают с осями координат, проходит через точки 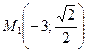 и
и  . Найти ее каноническое уравнение.
. Найти ее каноническое уравнение.
Решение. Напишем каноническое уравнение гиперболы
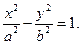
Этому уравнению удовлетворяют координаты точек 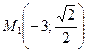 и
и  . Следовательно,
. Следовательно,
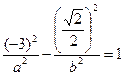 и
и 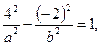
или
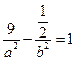 и
и 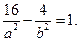
Отсюда находим 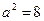 и
и 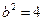 и подставляем их в каноническое уравнение гиперболы:
и подставляем их в каноническое уравнение гиперболы:
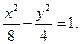
Парабола
Определение. Параболой называется геометрическое место точек плоскости, равноудаленных от данной точки 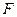 , называемой фокусом, и данной прямой, называемой директрисой. (Предполагается, что фокус не лежит на директрисе.)
, называемой фокусом, и данной прямой, называемой директрисой. (Предполагается, что фокус не лежит на директрисе.)
Обозначим расстояние от фокуса до директрисы через 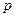 . Эта величина называется параметром параболы.
. Эта величина называется параметром параболы.
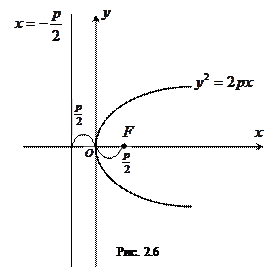
Выведем уравнение параболы. Расположим ось абсцисс так, чтобы она проходила через фокус перпендикулярно директрисе и имела положительное направление от директрисы к фокусу (рис. 2.6). За начало координат выберем середину перпендикуляра  , опущенного из фокуса на директрису. В выбранной таким образом системе координат фокус будет иметь координаты
, опущенного из фокуса на директрису. В выбранной таким образом системе координат фокус будет иметь координаты 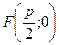 . Уравнение директрисы будет иметь следующий вид:
. Уравнение директрисы будет иметь следующий вид:
Пусть 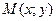 — точка параболы. По определению параболы, расстояние
— точка параболы. По определению параболы, расстояние  точки
точки 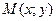 от директрисы равно ее расстоянию
от директрисы равно ее расстоянию 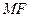 от фокуса:
от фокуса: 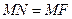 .
.
Из рис. 2.6 ясно, что  а
а 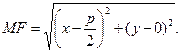 Следовательно,
Следовательно,
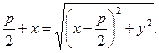
Возведя обе части этого уравнения в квадрат, получим

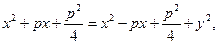
или, после упрощений:
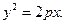
Полученное уравнение называется каноническим уравнением параболы. Ему, очевидно, удовлетворяют координаты любой точки параболы. Можно показать, что координаты точек, не лежащих на параболе, уравнению не удовлетворяют.
Парабола, определяемая уравнением 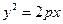 имеет вид, изображенный на рис. 2.6.
имеет вид, изображенный на рис. 2.6.
Ось симметрии параболы называется фокальной осью. Точка пересечения параболы с осью симметрии называется ее вершиной. В данном случае вершина параболы совпадает с началом координат.
Пример. Дана парабола  . Составить уравнение ее директрисы и найти ее фокус.
. Составить уравнение ее директрисы и найти ее фокус.
Решение. Сравнивая данное уравнение с каноническим уравнением параболы, видим, что 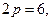
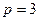 . Так как директриса параболы имеет уравнение
. Так как директриса параболы имеет уравнение 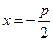 , а фокус — координаты
, а фокус — координаты 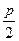 и
и  , то уравнение директрисы
, то уравнение директрисы  , а фокус
, а фокус 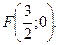
Замечание. Если фокальную ось параболы принять за ось ординат, то уравнение параболы примет вид
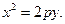
Уравнение второй степени вида
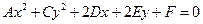
(не содержащее члена 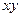 с произведением координат) называется пятичленным уравнением кривой второго порядка.
с произведением координат) называется пятичленным уравнением кривой второго порядка.
Причем, если 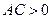 , то определяемая этим уравнением кривая есть эллипс.
, то определяемая этим уравнением кривая есть эллипс.
Если 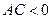 , то соответствующая кривая является гиперболой, которая может вырождаться в две пересекающиеся прямые, если левая часть уравнения распадается на произведение двух линейных множителей.
, то соответствующая кривая является гиперболой, которая может вырождаться в две пересекающиеся прямые, если левая часть уравнения распадается на произведение двух линейных множителей.
Если  (т.е. либо
(т.е. либо  , либо
, либо 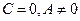 ), то уравнение определяет параболу, которая может вырождаться в две параллельные прямые, если левая часть уравнения не содержит либо
), то уравнение определяет параболу, которая может вырождаться в две параллельные прямые, если левая часть уравнения не содержит либо 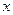 , либо
, либо 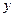 .
.
Вид кривой и расположение ее на плоскости легко устанавливаются
преобразованием пятичленного уравнения к виду 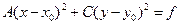 (т.е. группируем в скобки члены с одноименными координатами и дополняем выражения в скобках до полных квадратов). Затем переносим начало координат в точку
(т.е. группируем в скобки члены с одноименными координатами и дополняем выражения в скобках до полных квадратов). Затем переносим начало координат в точку 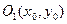 , сохраняя направление осей координат (параллельный перенос). Таким образом получаем канонический вид кривой второго порядка.
, сохраняя направление осей координат (параллельный перенос). Таким образом получаем канонический вид кривой второго порядка.
Пример. Уравнение кривой второго порядка путем выделения полного квадрата привести к каноническому виду:

Решение.
Преобразуем данное уравнение следующим образом:
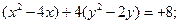
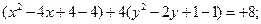

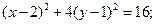

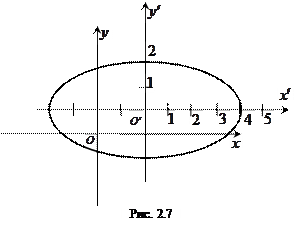
Произведем параллельный перенос осей координат, приняв за новое начало координат точку 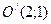 . Относительно новых осей уравнение кривой примет вид
. Относительно новых осей уравнение кривой примет вид 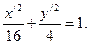 Таким образом, заданная кривая является эллипсом с полуосями
Таким образом, заданная кривая является эллипсом с полуосями 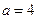 ;
; 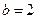 . (рис. 2.7).
. (рис. 2.7).
 Приведение к каноническому виду уравнения второй степени, содержащего член с произведением переменных, значительно сложнее. Этот вопрос подробно рассмотрен в литературе [1].
Приведение к каноническому виду уравнения второй степени, содержащего член с произведением переменных, значительно сложнее. Этот вопрос подробно рассмотрен в литературе [1].
В заключение этой темы рассмотрим два примера на определение уравнения геометрического места точек.
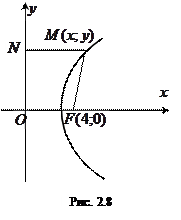 Пример. Составить уравнение геометрического места точек, одинаково удаленных от оси
Пример. Составить уравнение геометрического места точек, одинаково удаленных от оси 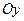 и от точки
и от точки 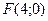 .
.
Решение. Пусть точка 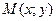 лежит на искомом геометрическом месте точек (черт. 2.8). Тогда согласно условию задачи
лежит на искомом геометрическом месте точек (черт. 2.8). Тогда согласно условию задачи  ,
, 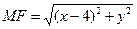 ,
,  .
.
В силу равенства

имеем:
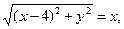
или
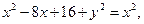
и окончательно: 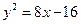 .
.
Искомое геометрическое место точек есть парабола, симметричная оси  и с фокусом в точке
и с фокусом в точке  (рис. 2.8).
(рис. 2.8).
Покажем, что координаты точки, не принадлежащей нашему геометрическому месту, т. е. параболе, не удовлетворяют найденному уравнению 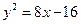 .
.
Предположим, что точка 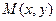 не принадлежит искомому геометрическому месту. Тогда либо
не принадлежит искомому геометрическому месту. Тогда либо  , либо
, либо 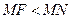 .
.
Пусть, например,  . Тогда
. Тогда 
После возведения в квадрат, раскрытия скобок и переноса всех членов влево, получим: 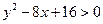 .
.
Следовательно, точка 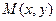 не удовлетворяет уравнению геометрического места
не удовлетворяет уравнению геометрического места 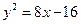 .
.
Для случая 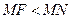 доказательство аналогично.
доказательство аналогично.
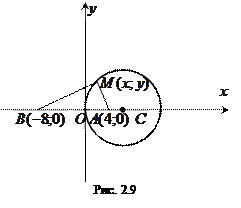 Пример. Определить траекторию точки
Пример. Определить траекторию точки  , которая движется так, что ее расстояние от точки
, которая движется так, что ее расстояние от точки  остается вдвое меньше расстояния от точки
остается вдвое меньше расстояния от точки  .
.
Решение. Пусть точка 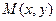 лежит на искомой траектории. Тогда, согласно условию,
лежит на искомой траектории. Тогда, согласно условию, 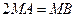 .
.
Расстояние 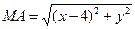 ,
,
расстояние 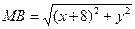 .
.
В силу равенства 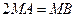 имеем:
имеем:
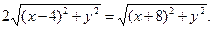
Возводим правую и левую части равенства в квадрат, получаем

После преобразования получим
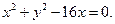
Таким образом, искомая траектория точки  — окружность (рис.2.9).
— окружность (рис.2.9).
Контрольная работа № 2 по теме
"АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ"
2.1. Даны три последовательные вершины параллелограмма 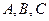 .
.
Найти:
1) уравнение стороны 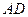 ;
;
2) уравнение высоты, опущенной из вершины  на сторону
на сторону 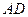 , длину этой высоты;
, длину этой высоты;
3) уравнение диагонали  ;
;
4) площадь параллелограмма;
5) угол между диагоналями параллелограмма;
2.1.1. 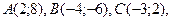
2.1.2. 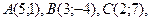
2.1.3. 
2.1.4. 
2.1.5. 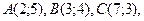
2.1.6. 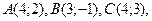
2.1.7. 
2.1.8. 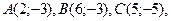
2.1.9. 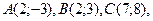
2.1.10. 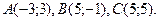
2.2. Задачи на уравнения прямой и плоскости в пространстве.
2.2.1. Даны две точки: 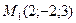 и
и  . Составить уравнение плоскости, проходящей через т.
. Составить уравнение плоскости, проходящей через т.  перпендикулярно к вектору
перпендикулярно к вектору 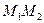 .
.
2.2.2. Составить уравнение плоскости, которая проходит через т. 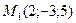 параллельно плоскости
параллельно плоскости 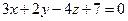 .
.
2.2.3. Составить канонические уравнения прямой, проходящей через т.  параллельно прямой
параллельно прямой 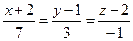 .
.
2.2.4. Составить уравнение плоскости, проходящей через т.  параллельно двум векторам:
параллельно двум векторам: 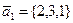 и
и 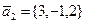 .
.
2.2.5. Составить уравнение плоскости, проходящей через три точки: 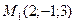 ,
, 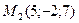 ,
, 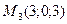 .
.
2.2.6. Составить уравнение прямой, проходящей через т. 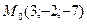 перпендикулярно к плоскости
перпендикулярно к плоскости 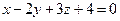 .
.
2.2.7. Найти угол между прямыми 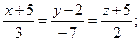

2.2.8. Составить уравнение плоскости, проходящей через т.


