 |
Двойной интеграл. Основные определения и свойства.
|
|
|
|
Касательная и нормаль к поверхности
Определение. Нормалью к поверхности в точке N0 называется прямая, проходящая через точку N0 перпендикулярно касательной плоскости к этой поверхности.
В какой – либо точке поверхность имеет, либо только одну касательную плоскость, либо не имеет ее вовсе.
Если поверхность задана уравнением z = f(x, y), где f(x, y) – функция, дифференцируемая в точке М0(х0, у0), касательная плоскость в точке N0(x0,y0,(x0,y0)) существует и имеет уравнение:
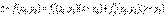 . Уравнение нормали к поверхности в этой точке:
. Уравнение нормали к поверхности в этой точке:

Геометрическим смыслом полного дифференциала функции двух переменных f(x, y) в точке (х0, у0) является приращение аппликаты (координаты z) касательной плоскости к поверхности при переходе от точки (х0, у0) к точке (х0+Dх, у0+Dу).
Как видно, геометрический смысл полного дифференциала функции двух переменных является пространственным аналогом геометрического смысла дифференциала функции одной переменной.
Пример. Найти уравнения касательной плоскости и нормали к поверхности

в точке М(1, 1, 1).
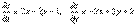

Уравнение касательной плоскости:
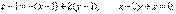
Уравнение нормали: 
Вычисление двойного интеграла в полярных координатах.
Пусть область D ограничена линией r = r() и лучами = и =, где и r – полярные координаты точки на плоскости, связанные с ее декартовыми координатами x и y
 соотношениями
соотношениями  (рис. 5). В этом случае
(рис. 5). В этом случае

Замечание. Если область D в декартовых координатах задается уравнением, содержащим бином  , например,
, например,  и т.д., то вычисление двойного интеграла по такой области удобнее производить в полярных координатах.
и т.д., то вычисление двойного интеграла по такой области удобнее производить в полярных координатах.
Двойной интеграл. Основные определения и свойства.
Двойные интегралы.
Рассмотрим на плоскости некоторую замкнутую кривую, уравнение которой
|
|
|
f(x, y) = 0.
y
Совокупность всех точек, лежащих внутри кривой и на самой кривой назовем замкнутой областью D. Если выбрать точки области без учета точек, лежащих на кривой, область будет называется незамкнутой область D.
С геометрической точки зрения D - площадь фигуры, ограниченной контуром.
Разобьем область D на n частичных областей сеткой прямых, отстоящих друг от друга по оси х на расстояние Dхi, а по оси у – на Dуi. Вообще говоря, такой порядок разбиения наобязателен, возможно разбиение области на частичные участки произвольной формы и размера.
Получаем, что площадь S делится на элементарные прямоугольники, площади которых равны Si = Dxi × Dyi.
В каждой частичной области возьмем произвольную точку Р(хi, yi) и составим интегральную сумму

где f – функция непрерывная и однозначная для всех точек области D.
Если бесконечно увеличивать количество частичных областей Di, тогда, очевидно, площадь каждого частичного участка Si стремится к нулю.
Определение: Если при стремлении к нулю шага разбиения области D интегральные суммы  имеют конечный предел, то этот предел называется двойным интегралом от функции f(x, y) по области D.
имеют конечный предел, то этот предел называется двойным интегралом от функции f(x, y) по области D.

С учетом того, что Si = Dxi × Dyi получаем:

В приведенной выше записи имеются два знака S, т.к. суммирование производится по двум переменным х и у.
Т.к. деление области интегрирования произвольно, также произволен и выбор точек Рi, то, считая все площади Si одинаковыми, получаем формулу:
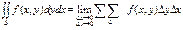
Условия существования двойного интеграла.
Сформулируем достаточные условия существования двойного интеграла.
Теорема. Если функция f(x, y) непрерывна в замкнутой области D, то двойной интеграл  существует
существует
Теорема. Если функция f(x, y) ограничена в замкнутой области D и непрерывна в ней всюду, кроме конечного числа кусочно – гладких линий, то двойной интеграл  существует.
существует.
|
|
|
Свойства двойного интеграла.
1) 
2) 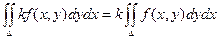
3) Если D = D1 + D2, то

4) Теорема о среднем. Двойной интеграл от функции f(x, y) равен произведению значения этой функции в некоторой точке области интегрирования на площадь области интегрирования.
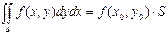
5) Если f(x, y) ³ 0 в области D, то  .
.
6) Если f1(x, y) £ f2(x, y), то  .
.
7)  .
.
№43 Определение Предположим, что кривая C задана векторной функцией  где переменная s − длина дуги кривой. Тогда производная векторной функции
где переменная s − длина дуги кривой. Тогда производная векторной функции
 представляет собой единичный вектор, направленный вдоль касательной к данной кривой (рисунок 1).
представляет собой единичный вектор, направленный вдоль касательной к данной кривой (рисунок 1).
В приведенной выше формуле α, β и γ − углы между касательной и положительными направлениями осей O x, O y и O z, соответственно.
Введем векторную функцию  , определенную на кривой C, так, чтобы для скалярной функции
, определенную на кривой C, так, чтобы для скалярной функции
 существовал криволинейный интегра
существовал криволинейный интегра  Такой интеграл
Такой интеграл  называется криволинейным интегралом второго рода от векторной функции
называется криволинейным интегралом второго рода от векторной функции  вдоль кривой C и обозначается как
вдоль кривой C и обозначается как

Таким образом, по определению, 
где  − единичный вектор касательной к кривой C.
− единичный вектор касательной к кривой C.
Последнюю формулу можно переписать также в векторной форме:

 где.
где.
Если кривая C лежит в плоскости O xy, то полагая R = 0, получаем
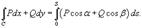 Свойства криволинейногоинтеграла второго рода
Свойства криволинейногоинтеграла второго рода
Криволинейный интеграл II рода обладает следующими свойствами: Пусть C обозначает кривую с началом в точке A и конечной точкой B. Обозначим через −C кривую противоположного направления - от B к A. Тогда 
Если C − объединение кривых C 1 и C 2 (рисунок 2 выше), то  Если кривая C задана параметрически в виде
Если кривая C задана параметрически в виде  , то
, то  Если кривая C лежит в плоскости O xy
Если кривая C лежит в плоскости O xy  и задана уравнениTм (предполагается, что R = 0 и t = x), то последняя формула записывается в виде
и задана уравнениTм (предполагается, что R = 0 и t = x), то последняя формула записывается в виде 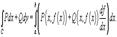
№49Поверхность F задана явно z = z(x,y), (x,y)Î D (компакт),
где z(x,y) имеет в D непрерывные частные производные первого порядка, фунуция f(x,y,z) определена и непрерывна на F. Тогда существует интеграл  , равный
, равный
 =
=  .
.
Доказательство. Для площадей  получаем
получаем
mFk= 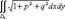 =
=  .
.
Тогда интегральные суммы будут равны
s = 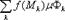 =
= 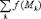
 =
= 
 +
+ 
 .
.
Первая из сумм является интегральной для  , вторая может быть сделана сколь угодно малой выбором достаточно мелкого разбиения. Последнее следует из равномерной непрерывности функции f(x,y,z(x,y)) на D.
, вторая может быть сделана сколь угодно малой выбором достаточно мелкого разбиения. Последнее следует из равномерной непрерывности функции f(x,y,z(x,y)) на D.
№40(продолжение) Достаточное условие существования криволинейного интеграла I рода будет сформулировано позже, когда покажем способ его вычисления.
|
|
|
Определение криволинейного интеграла I рода по структуре такое же, как и определение определенного интеграла. Поэтому криволинейный интеграл I рода обладает теми же свойствами, что и определенный интеграл. Приведем эти свойства без доказательства.
СВОЙСТВА КРИВОЛИНЕЙНОГО ИНТЕГРАЛА I РОДА
1. 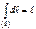 , где
, где  – длина кривой
– длина кривой  .
.
2. Постоянный множитель можно выносить за знак криволинейного интеграла I рода, т.е. 
3. Криволинейный интеграла I рода от алгебраической суммы двух (конечного числа) функций равен алгебраической сумме криволинейных интегралов I рода от этих функций, т.е.


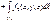 .
.
4. Если кривая  разбита на две части
разбита на две части  и
и 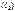 , не имеющие общих внутренних точек, то
, не имеющие общих внутренних точек, то
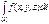


(свойство аддитивности криволинейного интеграла I рода).
5. Если всюду на кривой  функция
функция 
 (
(
 ), то
), то

 .
.
6. Если всюду на кривой 

 (
(
 ),
),
то 
 .
.
7. (следствие свойств 6 и 1) Если  и
и  – соответственно наименьшее и наибольшее значения функции
– соответственно наименьшее и наибольшее значения функции  на кривой
на кривой  , то
, то
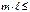

 ,
,
где  – длина кривой
– длина кривой  .
.
8. (теорема о среднем для криволинейного интеграла I рода) Если функция  непрерывна на кривой
непрерывна на кривой  [1], то найдется такая точка
[1], то найдется такая точка 
 , что справедливо равенство
, что справедливо равенство

 ,
,
где  – длина кривой
– длина кривой  .
.
№42Длина кривой.
Если подынтегральная функция f(x, y, z) ≡ 1, то из определения криволинейного интеграла 1-го рода получаем, что в этом случае он равен длине кривой, по которой ведется интегрирование:

Масса кривой.
Считая, что подынтегральная функция γ (x, y, z) определяет плотность каждой точки кривой, найдем массу кривой по формуле
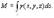
3. Моменты кривой l найдем, рассуждая так же, как в случае плоской области:  -
-
статические моменты плоской кривой l относительно осей Ох и Оу;
 -
-
момент инерции пространственной кривой относительно начала координат;
 -
-
· моменты инерции кривой относительно координатных осей.
4.Координаты центра масс кривой вычисляются по формулам
 .
.
№38(2) Замена переменных в тройных интегралах
При вычислении тройного интеграла, как и двойного, часто удобно сделать замену переменных. Это позволяет упростить вид области интегрирования или подынтегральное выражение.
|
|
|
Пусть исходный тройной интеграл задан в декартовых координатах x, y, z в области U:

Требуется вычислить данный интеграл в новых координатах u, v, w. Взаимосвязь старых и новых координат описывается соотношениями:

Предполагается, что выполнены следующие условия:
1.Функции φ, ψ, χ непрерывны вместе со своими частными производными;
2.Существует взаимно-однозначное соответствие между точками области интегрирования U в пространстве xyz и точками области U' в пространстве uvw;
3.Якобиан преобразования I (u,v,w), равный

отличен от нуля и сохраняет постоянный знак всюду в области интегрирования U.
Тогда формула замены переменных в тройном интеграле записывается в виде:

В приведенном выражении означает абсолютное значение якобиана.
№38 Тройные интегралы в сферических координатах
Сферическими координатами точки M(x,y,z) называются три числа − ρ, φ, θ, где
ρ − длина радиуса-вектора точки M;
φ − угол, образованный проекцией радиуса-вектора на плоскость Oxy и осью Ox;
θ − угол отклонения радиуса-вектора от положительного направления оси Oz (рисунок 1).
Рис.1 
Обратите внимание, что определения ρ, φ в сферических и цилиндрических координатах отличаются друг от друга.
Сферические координаты точки связаны с ее декартовыми координатами соотношениями

Якобиан перехода от декартовых координат к сферическим имеет вид:

Раскладывая определитель по второму столбцу, получаем
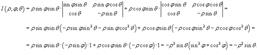
Соответственно, абсолютное значение якобиана равно

Следовательно, формула замены переменных при преобразовании декартовых координат в сферические имеет вид:

Тройной интеграл удобнее вычислять в сферических координатах, когда область интегрирования U представляет собой шар (или некоторую его часть) и/или когда подынтегральное выражение имеет вид f (x2 + y2 + z2).
№52
Поверхность
Выберем на гладкой поверхности (замк-нутой или ограниченной гладким контуром) точку М0 и проведем в ней нормаль к поверхности, выбрав для нее определенное направление (одно из двух возможных). Проведем по поверхности замкнутый контур, начинающийся и заканчивающийся в точке М0. Рассмотрим точку М, обходящую этот контур, и в каждом из ее положений проведем нормаль того направления, в которое непрерывно переходит нормаль из предыдущей точки. Если после обхода контура нормаль вернется в точке М0 в перво-начальное положение при любом выборе точки М0 на поверхности, поверхность называется двусторонней. Если же направление нормали после обхода хотя бы одной точки изменится на противоположное, поверхность называется односторон-ней (примером односторонней поверхности служит лист Мебиуса).Из вышесказанного следует, что выбор направления нормали в одной точке одно-значно определяет направление нормали во всех точках поверхности.
|
|
|
Определение
Совокупность всех точек поверхности содинаковымнаправлени-ем нормали называется стороной поверхности.
Ориентация поверхности.
Рассмотрим незамкнутую гладкую двустороннюю поверхность S, ограниченную контуром L, и выберем одну сторону этой поверхности.
Определение
Назовем положительным направление обхода контура L, при котором движение по контуру происходит против часовой стрелки относительно наблюдателя, находящегося в конечной точке нормали к какой-либо точке поверх-ности S, соответствующей выбранной стороне поверхности. Обратное направление обхода контура назовем отрицательным.
Поток векторного поля.
Рассмотрим векторное поле А(М), определенное в пространственной области G, ориентированную гладкую поверхность S G и поле единичных нормалей п(М) на выбранной стороне поверхности S.
Определение 13.3. Поверхностный интеграл 1-го рода 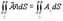 , (13.1)
, (13.1)
где An – скалярное произведение соответствующих векторов, а Ап – проекция вектора А на направление нормали, называется потоком векторного поля А(М) через выбранную сторону поверхности S.
Замечание 1.
Если выбрать другую сторону поверхности, то нормаль, а, следова-тельно, и поток изменят знак.
Замечание 2.
Если вектор А задает скорость течения жидкости в данной точке, то интеграл (13.1) определяет количество жидкости, протекающей в единицу времени через поверхность S в положительном направлении (отсюда общий термин «поток»).
№53 Поверхностный интеграл второго рода. Определение и св-ва.
Определение
Рассмотрим двустороннюю поверхность  , гладкую или кусочно-гладкую, и фиксируем какую-либо из двух ее сторон, что равносильно выбору на поверхности определенной ориентации.
, гладкую или кусочно-гладкую, и фиксируем какую-либо из двух ее сторон, что равносильно выбору на поверхности определенной ориентации.
Для определенности предположим сначала, что поверхность задана явным уравнением  причем точка
причем точка  изменяется в области
изменяется в области  на плоскости
на плоскости  , ограниченный кусочно-гладким контуром.
, ограниченный кусочно-гладким контуром.
Пусть теперь в точках данной поверхности  определена некоторая функция
определена некоторая функция  . Разбив поверхность сетью кусочно-гладких кривых на части
. Разбив поверхность сетью кусочно-гладких кривых на части  и выбрав на каждой такой части точку
и выбрав на каждой такой части точку  вычисляем значение функции
вычисляем значение функции 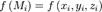 в данной точке и умножим его на площадь
в данной точке и умножим его на площадь  проекции на плоскость
проекции на плоскость 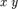 элемента
элемента  , снабженную определенным знаком. Составим интегральную сумму:
, снабженную определенным знаком. Составим интегральную сумму: 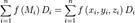
Конечный предел этой интегральной суммы при стремлении диаметров всех частей к нулю называют поверхностным интегралом второго рода от

распространенным на выбранную сторону поверхности  , и обозначают символом
, и обозначают символом

(здесь  ) напоминает о площади проекции элемента поверхности на плоскость
) напоминает о площади проекции элемента поверхности на плоскость 
Если вместо плоскости  спроектировать элементы поверхности на плоскость
спроектировать элементы поверхности на плоскость  или
или  , то получим два других поверхностных интеграла второго типа:
, то получим два других поверхностных интеграла второго типа:
 или
или 
В приложениях чаще всего встречаются соединения интегралов всех этих видов:
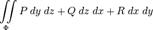
где  суть функции от
суть функции от  , определенные в точках поверхности
, определенные в точках поверхности  .
.
Связь между поверхностными интегралами второго и первого рода
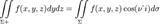
, где  — единичный вектор нормали поверхности
— единичный вектор нормали поверхности 
 — орт.
— орт.
Свойства
1. Линейность:  ;
;
2. Аддитивность:  ;
;
3. При изменении ориентации поверхности, поверхностный интеграл меняет знак.
№60 Опера́торна́бла (оператор Гамильтона) — векторный дифференциальный оператор, обозначаемый символом  (набла). Для трёхмерного евклидова пространства в прямоугольных декартовых координатах оператор набла определяется следующим образом:
(набла). Для трёхмерного евклидова пространства в прямоугольных декартовых координатах оператор набла определяется следующим образом:  где
где  — единичные векторы по осям x, y, z.
— единичные векторы по осям x, y, z.
Свойства оператора набла. Этот вектор приобретает смысл в сочетании со скалярной или векторной функцией, к которой он применяется.Если умножить вектор  на скаляр φ, то получится вектор
на скаляр φ, то получится вектор  который представляет собой градиент функции. Если вектор
который представляет собой градиент функции. Если вектор  скалярно умножить на вектор
скалярно умножить на вектор  , получится скаляр
, получится скаляр 
то есть дивергенция вектора  . Если
. Если  умножить на
умножить на  векторно, то получится ротор вектора
векторно, то получится ротор вектора  :
: 
Замечание: как и для обозначения скалярного и векторного произведения вообще, в случае их применения с оператором набла, наряду с использованными выше, часто используются эквивалентные им альтернативные обозначения, так, например, вместо  нередко пишут
нередко пишут  , а вместо
, а вместо  пишут
пишут  ; это касается и формул, приводимых ниже.
; это касается и формул, приводимых ниже.
Соответственно, скалярное произведение  есть скалярный оператор, называемый оператором Лапласа. Последний обозначается также
есть скалярный оператор, называемый оператором Лапласа. Последний обозначается также  . В декартовых координатах оператор Лапласа определяется следующим образом:
. В декартовых координатах оператор Лапласа определяется следующим образом:  Поскольку оператор набла является дифференциальным оператором, то при преобразовании выражений необходимо учитывать как правила векторной алгебры, так и правила дифференцирования. Например:
Поскольку оператор набла является дифференциальным оператором, то при преобразовании выражений необходимо учитывать как правила векторной алгебры, так и правила дифференцирования. Например: 
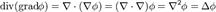
То есть производная выражения, зависящего от двух полей, есть сумма выражений, в каждом из которых дифференцированию подвергается только одно поле. Для удобства обозначения того, на какие поля действует набла, принято считать, что в произведении полей и операторов каждый оператор действует на выражение, стоящее справа от него, и не действует на всё, что стоит слева. Если требуется, чтобы оператор действовал на поле, стоящее слева, это поле каким-то образом отмечают, например, ставя над буквой стрелочку:  Такая форма записи обычно используется в промежуточных преобразованиях. Из-за её неудобства в окончательном ответе от стрелочек стараются избавиться.
Такая форма записи обычно используется в промежуточных преобразованиях. Из-за её неудобства в окончательном ответе от стрелочек стараются избавиться.
№61 Векторными дифференциальными операциями второго порядка называются следующие пять операций:
1.  где
где  - оператор Лапласа.
- оператор Лапласа.
- - - - - - - -- - - - - - - - - - - - - -
2 
. 
- - - - - - - - - - - - -
3. 
- - - - - - - - - - - - - - - - -
4. 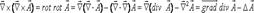 Здесь
Здесь  — это векторная величина, полученная в результате применения оператора Лапласа к каждой проекции вектора
— это векторная величина, полученная в результате применения оператора Лапласа к каждой проекции вектора  .
.
- - - - - - - - - - - - - - -
5. 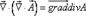 ;
; 

 - правильная рациональная дробь, знаменатель P(x) которой представлен в виде произведения линейных и квадратичных множителей (отметим, что любой многочлен с действительными коэффициентами может быть представлен в таком виде: P(x) = (x - a)a…(x - b)b(x2 + px + q)l…(x2 + rx + s)m ), то эта дробь может быть разложена на элементарные по следующей схеме:
- правильная рациональная дробь, знаменатель P(x) которой представлен в виде произведения линейных и квадратичных множителей (отметим, что любой многочлен с действительными коэффициентами может быть представлен в таком виде: P(x) = (x - a)a…(x - b)b(x2 + px + q)l…(x2 + rx + s)m ), то эта дробь может быть разложена на элементарные по следующей схеме:
 где Ai, Bi, Mi, Ni, Ri, Si – некоторые постоянные величины.
При интегрировании рациональных дробей прибегают к разложению исходной дроби на элементарные. Для нахождения величин Ai, Bi, Mi, Ni, Ri, Si применяют так называемый метод неопределенных коэффициентов, суть которого состоит в том, что для того, чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х.
Метод Остроградского— метод выделения рациональной части неопределенного интеграла от рациональной дроби, знаменатель которой — многочлен степени n с кратными корнями, а числитель — многочлен степени m< n-1. Согласно этому методу,
где многочлены Q1, Q2, P1, P2 имеют степени соответственно n1, n2, m1, m2, такие что n1 + n2 = n, m1< n1 — 1, m2< n2 — 1 и многочлен Q2(x) не имеет кратных корней. Таким образом, Q1(x) является наибольшим общим делителем многочленов Q(x) и, следовательно, его можно найти, используя алгоритм Евклида. Из этого равенства, дифференцируя, получаем тождество, которое позволяет найти явное выражение многочленов P1(x) и P2(x).
Метод Остроградского назван по имени М. В. Остроградского, впервые предложившего его в 1844 году.
№22 Функции нескольких переменных
При рассмотрении функций нескольких переменных ограничимся подробным описанием функций двух переменных, т.к. все полученные результаты будут справедливы для функций произвольного числа переменных.
Определение: Если каждой паре независимых друг от друга чисел (х, у) из некоторого множества по какому - либо правилу ставится в соответствие одно или несколько значений переменной z, то переменная z называется функцией двух переменных.
z = f(x, y)
Определение: Если паре чисел (х, у) соответствует одно значение z, то функция называется однозначной, а если более одного, то – многозначной.
Определение: Областью определения функции z называется совокупность пар (х, у), при которых функция z существует.
Определение: Окрестностью точкиМ0(х0, у0) радиуса r называется совокупность всех точек (х, у), которые удовлетворяют условию
где Ai, Bi, Mi, Ni, Ri, Si – некоторые постоянные величины.
При интегрировании рациональных дробей прибегают к разложению исходной дроби на элементарные. Для нахождения величин Ai, Bi, Mi, Ni, Ri, Si применяют так называемый метод неопределенных коэффициентов, суть которого состоит в том, что для того, чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х.
Метод Остроградского— метод выделения рациональной части неопределенного интеграла от рациональной дроби, знаменатель которой — многочлен степени n с кратными корнями, а числитель — многочлен степени m< n-1. Согласно этому методу,
где многочлены Q1, Q2, P1, P2 имеют степени соответственно n1, n2, m1, m2, такие что n1 + n2 = n, m1< n1 — 1, m2< n2 — 1 и многочлен Q2(x) не имеет кратных корней. Таким образом, Q1(x) является наибольшим общим делителем многочленов Q(x) и, следовательно, его можно найти, используя алгоритм Евклида. Из этого равенства, дифференцируя, получаем тождество, которое позволяет найти явное выражение многочленов P1(x) и P2(x).
Метод Остроградского назван по имени М. В. Остроградского, впервые предложившего его в 1844 году.
№22 Функции нескольких переменных
При рассмотрении функций нескольких переменных ограничимся подробным описанием функций двух переменных, т.к. все полученные результаты будут справедливы для функций произвольного числа переменных.
Определение: Если каждой паре независимых друг от друга чисел (х, у) из некоторого множества по какому - либо правилу ставится в соответствие одно или несколько значений переменной z, то переменная z называется функцией двух переменных.
z = f(x, y)
Определение: Если паре чисел (х, у) соответствует одно значение z, то функция называется однозначной, а если более одного, то – многозначной.
Определение: Областью определения функции z называется совокупность пар (х, у), при которых функция z существует.
Определение: Окрестностью точкиМ0(х0, у0) радиуса r называется совокупность всех точек (х, у), которые удовлетворяют условию  .
№6. Определение: Биноминальным дифференциаломназывается выражение
xm(a + bxn)pdx
где m, n, и p – рациональные числа.
Как было доказано академиком Чебышевым П.Л. (1821-1894), интеграл от биноминального дифференциала может быть выражен через элементарные функции только в следующих трех случаях:
1) Если р – целое число, то интеграл рационализируется с помощью подстановки
.
№6. Определение: Биноминальным дифференциаломназывается выражение
xm(a + bxn)pdx
где m, n, и p – рациональные числа.
Как было доказано академиком Чебышевым П.Л. (1821-1894), интеграл от биноминального дифференциала может быть выражен через элементарные функции только в следующих трех случаях:
1) Если р – целое число, то интеграл рационализируется с помощью подстановки
 , где l - общий знаменатель m и n.
2) Если
, где l - общий знаменатель m и n.
2) Если  - целое число, то интеграл рационализируется подстановкой
- целое число, то интеграл рационализируется подстановкой
 , где s – знаменатель числа р.
3) Если
, где s – знаменатель числа р.
3) Если  - целое число, то используется подстановка
- целое число, то используется подстановка  , где s – знаменатель числа р.
Однако, наибольшее практическое значение имеют интегралы от функций, рациональных относительно аргумента и квадратного корня из квадратного трехчлена.
На рассмотрении этих интегралов остановимся более подробно.
Интегралы вида
, где s – знаменатель числа р.
Однако, наибольшее практическое значение имеют интегралы от функций, рациональных относительно аргумента и квадратного корня из квадратного трехчлена.
На рассмотрении этих интегралов остановимся более подробно.
Интегралы вида 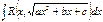 .
Существует несколько способов интегрирования такого рода функций. В зависимости от вида выражения, стоящего под знаком радикала, предпочтительно применять тот или иной способ.
Как известно, квадратный трехчлен путем выделения полного квадрата может быть приведен к виду:
.
Существует несколько способов интегрирования такого рода функций. В зависимости от вида выражения, стоящего под знаком радикала, предпочтительно применять тот или иной способ.
Как известно, квадратный трехчлен путем выделения полного квадрата может быть приведен к виду:
 Таким образом, интеграл приводится к одному из трех типов:
1)
Таким образом, интеграл приводится к одному из трех типов:
1)  2)
2)  3)
3)  №10 Теорема: (Теорема Ньютона – Лейбница)
Если функция F(x) – какая- либо первообразная от непрерывной функции f(x), то
№10 Теорема: (Теорема Ньютона – Лейбница)
Если функция F(x) – какая- либо первообразная от непрерывной функции f(x), то
 это выражение известно под названием формулы Ньютона – Лейбница.
Доказательство: Пусть F(x) – первообразная функции f(x). Тогда в соответствии с приведенной выше теоремой, функция
это выражение известно под названием формулы Ньютона – Лейбница.
Доказательство: Пусть F(x) – первообразная функции f(x). Тогда в соответствии с приведенной выше теоремой, функция  - первообразная функция от f(x). Но т.к. функция может иметь бесконечно много первообразных, которые будут отличаться друг от друга только на какое – то постоянное число С, то
- первообразная функция от f(x). Но т.к. функция может иметь бесконечно много первообразных, которые будут отличаться друг от друга только на какое – то постоянное число С, то
 при соответствующем выборе С это равенство справедливо для любого х, т.е. при х = а:
при соответствующем выборе С это равенство справедливо для любого х, т.е. при х = а:

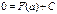
 Тогда
Тогда  .
А при х = b:
.
А при х = b:  Заменив переменную t на переменную х, получаем формулу Ньютона – Лейбница:
Заменив переменную t на переменную х, получаем формулу Ньютона – Лейбница:
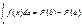 Теорема доказана..
Свойства определенного интеграла.
1)
Теорема доказана..
Свойства определенного интеграла.
1)  2)
2)  3)
3)  4) Если f(x) £ j(x) на отрезке [a, b] a < b, то
4) Если f(x) £ j(x) на отрезке [a, b] a < b, то  5) Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b], то:
5) Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b], то:
 №12-14 Несобственные интегралы.
Пусть функция f(x) определена и непрерывна на интервале [a, ¥). Тогда она непрерывна на любом отрезке [a, b].
Определение: Если существует конечный предел
№12-14 Несобственные интегралы.
Пусть функция f(x) определена и непрерывна на интервале [a, ¥). Тогда она непрерывна на любом отрезке [a, b].
Определение: Если существует конечный предел  , то этот предел называется несобственным интегралом от функции f(x) на интервале [a, ¥).
Обозначение:
, то этот предел называется несобственным интегралом от функции f(x) на интервале [a, ¥).
Обозначение:
 Если этот предел существуетиконечен, то говорят, что несобственный интеграл сходится.
Если предел не существует или бесконечен, то несобственный интеграл расходится.
Аналогичные рассуждения можно привести для несобственных интегралов вида:
Если этот предел существуетиконечен, то говорят, что несобственный интеграл сходится.
Если предел не существует или бесконечен, то несобственный интеграл расходится.
Аналогичные рассуждения можно привести для несобственных интегралов вида:

 Конечно, эти утверждения справедливы, если входящие в них интегралы существуют.
(14)Если этот предел существуетиконечен, то говорят, что несобственный интеграл сходится.
Если предел не существует или бесконечен, то несобственный интеграл расходится.
№21 Формула трапеций.
Эта формула является более точной по
сравнению с формулой прямоугольников. Подинтегральная функция в этом случае заменяется на вписанную ломаную.
Геометрически площадь криволинейной трапе
Конечно, эти утверждения справедливы, если входящие в них интегралы существуют.
(14)Если этот предел существуетиконечен, то говорят, что несобственный интеграл сходится.
Если предел не существует или бесконечен, то несобственный интеграл расходится.
№21 Формула трапеций.
Эта формула является более точной по
сравнению с формулой прямоугольников. Подинтегральная функция в этом случае заменяется на вписанную ломаную.
Геометрически площадь криволинейной трапе|
|
|


