Задачи на расчет течения газа при наличии энергообмена.

Курсовая работа

Расчет течений газа при наличии энергообмена.

 

Выполнил студент III курса мехмата:

Закиев Р.Н.

Научный руководитель:

Филатов Е.И.

 

 

Казань 2003.

 

Движение подогреваемого газа по трубе постоянного сечения.

Процесс подвода тепла вносит особый вид сопротивления: при подогреве движущегося газа полное давление падает. Будем рассматривать движение газа в трубке изображенной на рисунке:

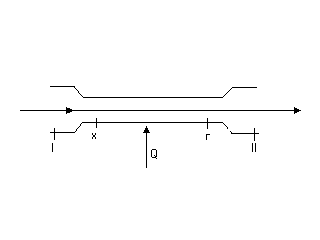
Прибегнем к следующей идеализированной схеме. Газ поступает в трубу х-г из канала с большим поперечным сечением. Пусть скорость потока мала. l_Х<<1, l_Г<<1.

Согласно уравнению Бернулли

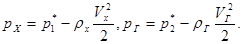
Отсюда изменение полного давления

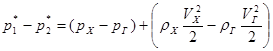(1).

Из уравнения неразрывности 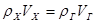следует,что если вследствие подогрева плотность газа уменьшается, то скорость его растет и, следовательно, статическое давление падает.

Из уравнения импульсов можно определить падение статического давления при подогреве на участке х-г (пренебрегая трением):

.

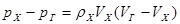
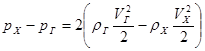Подставив эту разность в уравнение (1), имеем

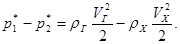Отсюда видно, что при подогреве медленно движущегося газа величина потерь мала. При значительной же скорости ими пренебрегать уже нельзя.

Обнаруженное “тепловое сопротивление” можно объяснить так: как известно, повышение энтропии в газе зависит как от количества подведенного тепла, так и от температурного уровня:

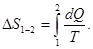При одном и том же количестве тепла прирост энтропии, а следовательно, и потери тем больше, чем ниже средняя температура процесса, т.е. чем выше скорость потока.

Оценим влияние подвода тепла на расход газа в трубе. Отношение расходов газа при наличии и отсутствии подогрева в трубе:

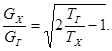Как видим подвод тепла при заданном перепаде давлений ведет к уменьшению расхода газа при одновременном увеличении скорости истечения.

Исследуем теперь падение давления на участке х-г трубы при большой дозвуковой скорости движения газа.

При значительных скоростях течения плотность газа при подогреве уменьшается не только из-за повышения температуры, но и вследствие понижения статического давления.В связи с этим скорость газа увеличивается вдоль трубы быстрее, чем температура. Скорость звука, которая пропорцианальна корню квадратному из абсолютной температуры, увеличивается вдоль трубы значительно медленнее, чем скорость потока. По этой причине число М=V/a по длине трубы растет.

Поток имеющий любую начальную скорость, можно за счет соответствующего подогрева довести до критической скорости(М_Г=1). При большом начальном значении числа М понадобится незначительный подогрев. Чем ниже скорость, тем более сильный критически й подогрев необходим. Но никаким подогревом нельзя перевести поток в цилиндрической трубе в сверхзвуковую область. Это явление носит название теплового кризиса.

Естественно, после того, как в конце трубы достигнут кризис, скорость потока в начале трубы не может быть увеличена никакими способами. Если по достижении кризиса продолжать подогрев газа, то величина критической скорости в конце трубы растет, а скорость в начале трубы падает. Иначе говоря, заданному количеству тепла соответствует совершенно определенное предельное значение числа М в начале трубы. Величины l и М связаны следующим соотношением: .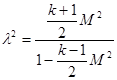

Задачи на расчет течения газа при наличии энергообмена.

I задача. (Давидсон В. Е. “Основы газовой динамики в задачах”. Задача№169)

(Все формулы использованные при решении задач взяты из задачника Давидсона В.Е.)

Постановка задачи:

Поток воздуха подогревается в цилиндрической трубе сжиганием в нем горючего, расход которого составляет 5% от расхода воздуха. До подогрева скорость воздуха V₁=50 м/сек, давление р₁=9,89 ата, температура торможения Т₀₁=400⁰К.Найти скорость и давление газа в сечении трубы,где температура торможения Т₀₂=1500⁰К.Принять к=1,33, R=291 дж/кг*град. Трением пренебречь.

Решение задачи:

Воспользуемся теоремой импульсов переписанной (для труб с прямолинейной осью) в скалярной форме:

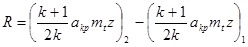                                              (1)

Применим ее в виде теоремы сохранения импульсов, т.е. при 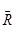=0.Откуда:

                                                        (2)

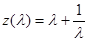здесь                                                                              (3)

-газодинамическая функция,

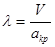                                                                                              (4)

l-коэффициент скорости,l₁ - коэффициент скорости на входе,l₂- коэффициент скорости на выходе из трубы.

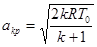                                                                                   (5)

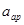-критическая скорость звука, G_t-секундный расход газа.

Найдем 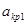 и 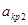.Так как для воздуха к=1,4 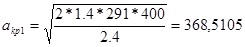м/сек.

Внутри трубы к=1,33

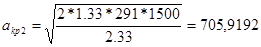м/сек.

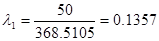. Так как расход G_t2 больше G_t1 на 5% то . z(l₁)=7.5049.Подставим найденные значения в формулу (2)

z(l₂)=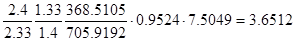

 

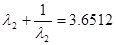.Решив уравнение найдем два значения l_2.

l₂=0,29825

l₂=3,35295

Реальным будет только первое решение, поскольку подогревом нельзя перевести дозвуковой поток в сверхзвуковой. Зная коэффициент скорости мы можем найти скорость, этому коэффициенту соответствующую:

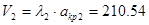м/сек.

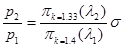                                                                            (6)

где по уравнению расхода

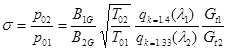                                                  (7)

s-коэффициент восстановления полного давления. p-газодинамическая функция. B_1G и B_2G здесь постоянные.

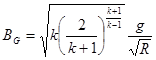                                                                     (8)

Вычисляем B_1G и B_2G по формуле (8):

B_1G=0,3937 и B_2G=0,3868.Найдем значения q_k=1.4(l₁), q_k=1,33(l₂), p_л=1,4(l₁), и p_л=1,4(l₁) по таблицам газодинамических функций: q_k=1.4(l₁)=0,2036, q_k=1,33(l₂)=0,4443, p_л=1,4(l₁)=0,9886, p_л=1,4(l₁) =0,9496.Подставим все найденные значения в формулы (6),(7) и (8).Найдем из формулы (6) р₂: р₂=9,0126 ата.

 

Ответ:V₂=210.54 м/сек, р₂=9,0126 ата.

 

II задача. (Давидсон В. Е. Основы газовой динамики в задачах. Задача№170).

Постановка задачи:

Сделать одномерный расчет степени подогрева, скорости воздуха и поперечных размеров для полутеплового сопла (тепловое воздействие на дозвуковую часть потока в цилиндрической трубе, геометрическое—на сверхзвуковую) по следующим данным: до подогрева в камере температура торможения Т₀₁=289⁰ К, давление торможения р₀₁=20 ата, скорость потока V₁=62,2 м/сек, секундный весовой расход воздуха через сопло Gt=9 кг/сек, истечение расчетное в атмосферу при давлении р_а=1,03 ата. Определить тягу сопла R.

Решение задачи:

В конце камеры подогрева воздух должен иметь критическую скорость. 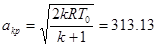 м/сек. При известной критической скорости и начальной скорости на входе в цилиндрическую часть сопла можно вычислить l₁. l₁-коэффициент скорости на входе в трубу. l₁=V/a_kp=0.1999. Т.к. в конце трубы воздух имеет критическую скорость, l на выходе из трубы-l₂=1. По теореме сохранения полного импульса

,

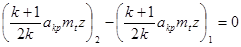в цилиндрической части  Из этой формулы находим температуру торможения на выходе из трубы:Т₀₂=1955⁰ К При известной температуре торможения можем найти скорость воздуха на выходе из цилиндрической части сопла: V₂=809.24 м/сек. Та же теорема,выраженная через газодинамическую функцию f(l), дает коэффициент восстановления полного давления s= 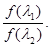=0,8066. Уравнение p(l_а)=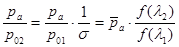 определяет коэффициент скорости в конце расширяющейся части сопла l_а и, следовательно, 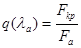. p(l_а)=0,0638. По газодинамическим таблицам находим значение l_а=1,81.Найдем скорость потока V_а=1464м/сек. Площадь поперечного сечения можно найти по формуле ,

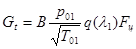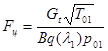=0,00198 м².F_ц - площадь поперечного сечения дозвуковой части сопла. Отсюда диаметр сечения дозвуковой части сопла: d_ц=88 мм. q(l_a)=0.3965. F_a - площадь поперечного сечения сверхзвуковой части сопла.

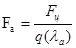
 F_a=0,0049936м². Диаметр сечения сверхзвуковой части сопла: d_а=135мм. Тягу сопла найдем по уравнению импульсов в форме .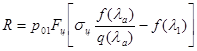

R=2154 H.

Ответ: Т₀₂=1955⁰ К V₂=809.24 м/сек,V_а=1464м/сек,d_ц=88 мм, d_а=135мм,R=2154Н

 

 

Список использованной литературы:

1) Давидсон В. Е. “Основы газовой динамики в задачах”. Издательство “Высшая школа” Москва-1965г,

2) Г.Н.Абрамович “Прикладная газовая динамика”. Издательство “Наука” Москва-1976г.

Поделиться:

Воспользуйтесь поиском по сайту: