 |
Индексация элементов массивов
|
|
|
|
Порядковый номер элемента, который является его адресом, называется индексом. Напоминаем, что нижняя граница индексации задается значением системной переменной ORIGIN, которая может принимать значение 0 или 1.
Имя массива естественно увязать с именами индексированных переменных, значениями которых являются элементы массива. Для этого достаточно в виде подстрочного индекса указать индекс элемента. Например, если третий из представленных массивов имеет имя V, то его элементами при ORIGIN=0 будут индексированные переменные:
Vo=0 V1=x V2=2x2 Vз-Зх3 V4=4x4
Векторы могут быть двух типов: векторы-строки и векторы-столбцы. Например:
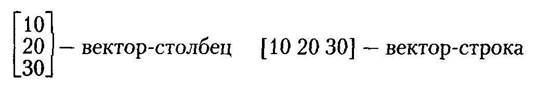
Несмотря на то что два этих вектора имеют одни и те же числовые значения элементов, они различны по типу и дадут разные результаты при векторных и матричных операциях, чувствительных к типу векторов.
Матрицы
Матрица может рассматриваться как совокупность ряда векторов одинаковой длины, например:
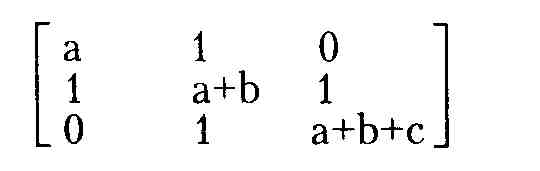
Элементы матриц являются индексированными переменными, имена которых совпадают с именами матриц. Но в этом случае для каждой индексированной переменной указываются два индекса: один — для номера строки, другой — для номера столбца. Например, для указанной матрицы М средний элемент обозначается как М1,1, а последний как М;2,2
Для задания векторов и матриц можно воспользоваться операцией Matrix... (Матрицы...) в позиции Math (Математика) основного меню, нажав клавиши Ctrl+V или введя пиктограмму с изображением шаблона матрицы. Это вызывает вначале появление диалогового окна, в котором надо указать размерность матрицы, т. е. количество ее строк т и столбцов п. Для векторов один из этих параметров должен быть равен 1. При m=1 получим вектор-столбец, а при п=\ — вектор-строку. Матрица является двумерным массивом с числом элементов тхп. Элементы векторов и матриц помещаются между большими квадратными скобками.
|
|
|
Ввод элементов векторов и матриц
Для указания подстрочных индексов после имени переменной вводится знак открывающей квадратной скобки:
Ввод Изображение в окне
V3 [ 2: V32 :=
Для элементов матрицы подстрочные индексы вводятся в круглых скобках с разделением их запятыми:
Ввод Изображение в окне редактирования
М [ (1, 2): M1,2: =
Индексы могут иметь только целочисленные значения Они могут начинаться с нуля или с целого числа, например с единицы, в соответствии со значением системной переменной ORIGIN
Задание векторов и матриц
В отношении индексированных переменных действуют те же правила присваивания и вывода, что и для обычных В частности, с помощью операций присваивания можно создать вектор или матрицу заданной размерности и заданного типа без ручного вывода их шаблоном и без их заполнения. Это иллюстрирует рис. 11. 4, на котором показано задание нулевой, единичной и специальной матриц путем поэлементного их формирования.
Рис. 11. 4 Задание матриц без применения их шаблонов

Такой способ задания матриц очень напоминает применяемый в обычных программах метод, при котором значения элементам матриц присваиваются в двух вложенных циклах с управляющими переменными и г. Однако это сходство чисто внешнее, так как в нашем случае ранжированные переменные i и j — векторы.
Данные файлового типа
Еще один важный тип данных системы MathCAD — файловые данные В сущности, это те же векторы и матрицы, но с элементами, которые могут записываться в виде файлов, имеющих свои имена. Файлы данных в системе представляет собою запись матриц в их естественной форме как последовательных текстовых файлов. Это простейший тип файлов, который легко обрабатывается в программах на различных языках программирования и может создаваться такими программами, благодаря чему возможен обмен данными между системой MathCAD и другими программами.
|
|
|
В ходе создания файла система считывает значения элементов векторов и матриц поэлементно (для матриц слева направо и сверху вниз) и по ходу считывания преобразует числовые значения элементов в их символьные эквиваленты, использующие ASCII-коды цифр и символы, относящиеся к заданию чисел. Эти символьные значения и записываются в виде данных файлов.
Существует семь файловых операций, рассматриваемых ниже. Создаваемые или используемые ими файлы легко просмотреть любым текстовым редактором, воспринимающим тексты в виде ASCII-кодов. При считывании файлов система обеспечивает обратное преобразование символьных представлений значений элементов в их числовые значения. Начнем рассмотрение этих операций с операции считывания файла, содержащего данные векторы.
READ (Имя_файла)
Эта операция-функция считывает данные из файла с указанным именем Имя_файла и возвращает значение — вектор. Обычно она используется для присваивания значений векторам, например:
V: = READ (DATA)
Здесь элементы вектора V получают значения, считанные из файла с именем DATA. Естественно, что такой файл должен существовать на диске, иначе ситуация будет считаться ошибочной. Для указания полного имени файла (если он не в текущем каталоге системы) следует использовать общеупотребительные для MS-DOS составные имена, например D: \EXPER\DATA, если файл DATA расположен на диске D в каталоге EXPER.
WRITE (Имя_файла)
Эта операция записывает данные в файл и присваивает ему указанное имя. Данные могут порождаться математическим выражением, например:
WRITE (Имя_файла): = Выражение
Разумеется, выражение должно создавать данные векторного типа.
APPEND (Имя_файла)
Эта операция подобна операции WRITE, но она дописывает данные в конец уже существующего файла. Нельзя использовать другие функции для до-писывания данных, поскольку эти функции уничтожают прежние данные в файле и заносят новые.
READPRN (Имя_файла)
Эта операция подобна READ, но считывает данные в виде двумерного массива — матрицы. Функция READPRN возвращает матрицу, значения элементов которой однозначно связаны со значениями элементов файла. Точнее, каждая строка или столбец возвращаемой матрицы подобны соответствующим строкам или столбцам текстового представления файла.
|
|
|
WRITEPRN (Имя_файла)
Эта операция подобна WRITE, но применяется для записи матричного выражения (или матрицы) в файл с указанным именем. Структура файла подобна структуре матрицы.
APPENDPRN (Имя_фaйлa)
|
|
|


