 |
Элементы теории вероятностей
|
|
|
|
Министерство образования РЕСПУБЛИКИ БАШКОРТОСТАН
Государственное автономное профессиональное образовательное учреждение
Уфимский колледж предпринимательства, экологии и дизайна
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
По выполнению контрольной работы
По дисциплине «математика»
Для студентов заочного отделения
Аннотация
Пособие предназначено для оказания помощи студентам заочного отделения при выполнении контрольной работы по математике или по элементам высшей математики. Пособие включает в себя разделы, имеющиеся в этих курсах.
Содержание
1. Дифференциальное исчисление.
2. Интегральное исчисление.
3. Элементы дискретной математики.
4. Численное интегрирование
5. Элементы теории вероятностей.
6. Ряды
7. Литература.
Дифференциальное исчисление
Изучить по учебной литературе вопросы:
1. Производная функция: определение, свойства, таблица производных. 
2. Исследование функции на монотонность.
3. Исследование функции на выпуклость (вогнутость) и точки перегиба.
4. Исследование функции на экстремум.
5. Геометрический и механический смыслы производной.
6. Построение графика функции, используя схему исследования свойств.
Примеры решения задач
1. Найти производные функций:
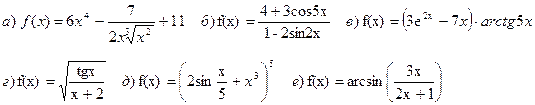
Решение
При выполнении дифференцирования будем использовать свойства производных, таблицу производных, правило дифференцирования сложных функций.
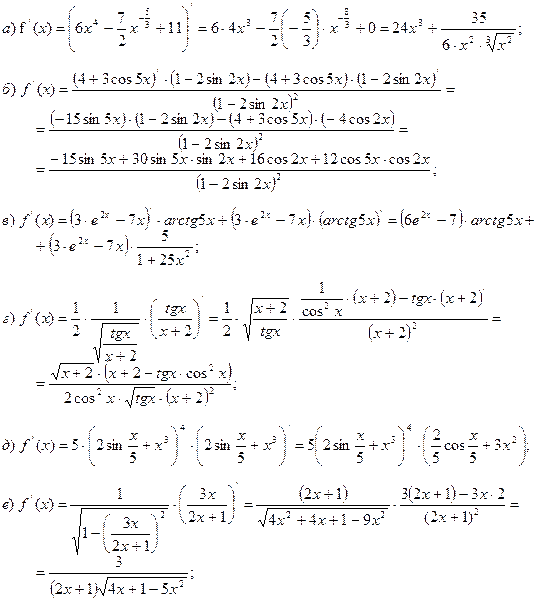
2. Выполнить исследование свойств функции по первой и второй производным и построить график функции f(x)=x3 - 3x2 - 45x + 20
Решение
Воспользуемся некоторыми пунктами исследования функции:
1)Областью определения этой функции является множество всех действительных чисел. Эта функция не является четной или нечетной. График этой функции не имеет асимптот.
|
|
|
2) Найдем первую производную и определим соответствующие свойства
функции. f’(x)=3x2 – 6x –45. Решим уравнение 3х2 – 6х – 45 = 0. Корнями уравнения являются числа (-3) и 5.
Воспользуемся таблицей:
| х | (-¥; -3) | -3 | (-3;5) | (5;¥) | |
| f’(x) | + | - | + | ||
| f(x) | 
| max | 
| min | 
|
Функция возрастает в интервалах (-¥;-3) и (5;¥), убывает в интервале (-3; 5).
Функция имеет максимальное значение f(-3)=101, имеет минимальное значение f(5)= - 155.
3) Найдем вторую производную f”(x)=(3x2 – 6x –45)’=6x-6.
Решим уравнение 6х-6=0. Решением уравнения является х=1.
Для определения свойств функции воспользуемся таблицей:
| х | (-¥; 1) | (1;¥) | |
| f”(x) | - | + | |
| f(x) | Ç выпуклая | точка перегиба | È вогнутая |
4) Для построения графика функции воспользуемся результатами вычислений, оформленными в виде таблицы:
| х | - 6 | -5 | -3 | - 1 | |||||||
| f(x) | - 34 | - 27 | -74 | -144 | -155 | -99 | |||||
| max | пер. | min |
Интегральное исчисление
Изучить по учебной литературе вопросы:
1. Неопределенный интеграл: определение, свойства, таблица интегралов.
2. Способы вычисления неопределенного интеграла: непосредственное интегрирование, способ подстановки.
3. Определенный интеграл: определение, свойства, геометрический смысл.
4. Способы вычисления определенного интеграла.
5. Применение определенного интеграла к решению практических задач: вычисление площадей плоских фигур.
Примеры решения задач
1) Найти неопределенные интегралы:
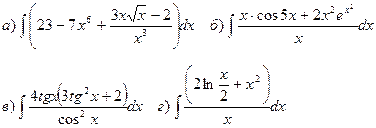
Решение
При решении примеров следует пользоваться свойствами неопределенных интегралов, таблицей интегралов, в которую включена формула интеграла функции линейного аргумента, непосредственным интегрированием и методом подстановки.
|
|
|
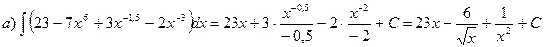
б) Выполнив почленное деление в подынтегральной функции, получим:
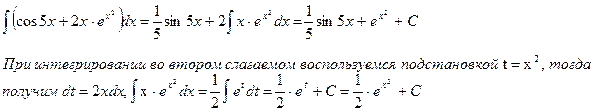
в)
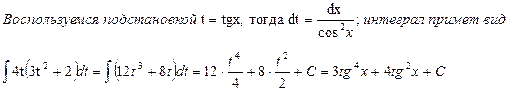
г) Будем использовать подстановку:
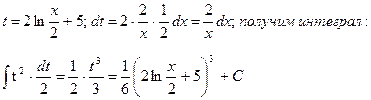
д) Воспользуемся подстановкой:
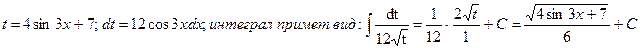
2) Вычислить определенные интегралы:
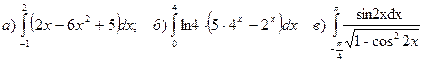
Решение
При вычислении определенных интегралов используем формулу Ньютона-Лейбница
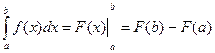. Получение первообразной функции F(x) будем выполнять или непосредственно или способом подстановки.
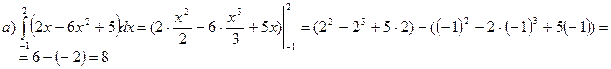
б)
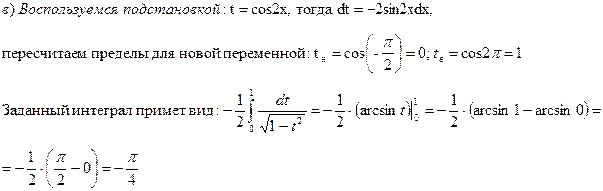
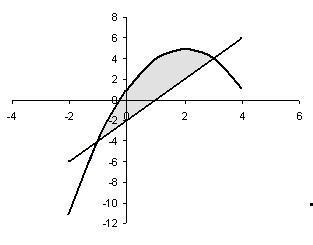
3. Найти площадь фигуры, ограниченной линиями: у=1 – х2 + 4х и 2х – у – 2 =0
Для определения точек пересечения линий составим уравнение из равенства выражений этих линий: 1 – х2 + 4х = 2х – 2; получим уравнение: х2 – 2х – 3 = 0.
Корнями этого уравнения являются числа: (-1) и 3. Для построения линий найдем
значения функций и составим их таблицы:
| х | -1 | х | -1 | ||||||
| у1 | -4 | у2 | -4 |
Построив фигуру на плоскости, вычислим ее площадь, определив значение интеграла
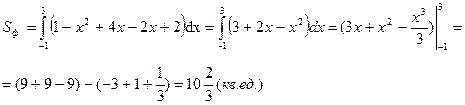
Дискретная математика
Изучить по учебной литературе вопросы:
1. Множества, их виды, способы задания.
2. Простейшие действия над множествами.
3. Отношения, их некоторые виды.
4. Графы, их основные элементы.
5. Некоторые виды графов.
Упражнения и их решение.
1) Составить объединение, пересечение и разность двух множеств.
а) А={3; 4; 6; 7}, B={2; 3; 4; 5}
AÈB={2; 3; 4; 5; 6; 7}, AÇB={3; 4}, A \ B ={6; 7}
б) А=(-1; 3]; B=[1; 5]
AÈB=(-1;5]; AÇB=[1; 3]; A \ B=(-1; 1)
В этом упражнении решение следует сопровождать рисунками.
Численное интегрирование
Определенным интегралом функции f(x), взятом в интервале от a до b, называется предел, к которому стремится интегральная сумма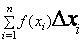 
при стремлении всех промежутков ∆xi к нулю
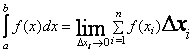
При приближенном вычислении определенного интеграла шаг интегрирования h=∆x выбирается конечным: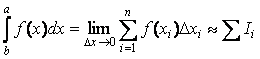 
, где Ii - элемент интегральной суммы. Заменяя подынтегральную функцию на каждом шаге отрезками линий нулевого, первого и второго порядков, получаем приближенные формулы для вычисления интеграла методами прямоугольников, трапеций и Симпсона соответственно.
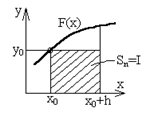
Правило прямоугольников (n=0). Заменяем график функции F(x) горизонтальной линией (линий нулевого порядка) и вычисляем значение элемента интегральной суммы как площадь прямоугольника
|
|
|
, где h - шаг интегрирования, у0 - значение функции в точке х=х0
у(х0)=у0
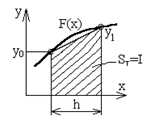
Правило трапеций (n=1). Заменяем график функции F(x) прямой, проходящей через две точки (х0,у0) и (х0+h,у1), и вычисляем значение элемента интегральной суммы как площадь трапеции
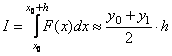
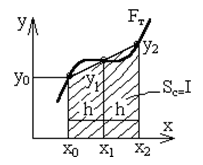
Правило Симпсона (n=2). Заменяем график функции F(x) квадратичной параболой, проходящей через три точки с координатами (х0,у0), (х0+h,у1), (х0+2h,у2). Расчетную формулу для вычисления элемента интегральной суммы получим, используя интерполяционный многочлен Лагранжа, в виде
y(x)=y0A0(x)+y1A1(x)+y2A2(x), где
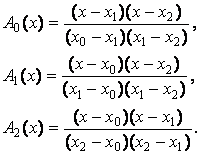
При x0=0; x1=h; x2=2h, получим
При интегрировании на отрезке [a,b] расчетные формулы для методов прямоугольника, трапеций и Симпсона имеют вид
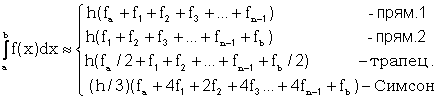
где h - шаг по x, fa, fi, fb - значения функции при x равном a, xi, b соответственно. Для метода прямоугольников приведены две расчетные формулы, так как площадь прямоугольника на каждом шаге интегрирования может определяться по левой или правой стороне. Суть метода прямоугольников для отрезка [a,b] проиллюстрирована на рисунке, при этом площадь под кривой f(x) (вспомните геометрический смысл определенного интеграла) заменена суммой площадей заштрихованных прямоугольников.
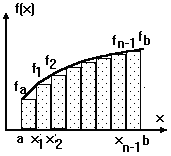
Рис. Численное интегрированние методом прямоугольников
Пример. Вычислить определенный интеграл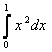 
четырьмя численными методами, сравнить с точным значением.
Этапы решения задачи приведены в таблице
Таблица
| N | Этап программирования | Выполнение |
| 1. | Постановка задачи | Вычислить определенный интеграл четырьмя численными методами и сравнить с точным значением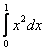 
|
| 2. | Математическое описание | Аналитическое решение:
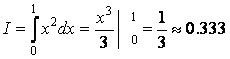Численное решение:
выполнить самостоятельно
|
Элементы теории вероятностей
Изучить по учебной литературе вопросы:
1. Случайные события, их виды.
2. Вероятность случайного события, способы ее получения.
3. Комбинаторика. Применение элементов комбинаторики к вычислению вероятности.
|
|
|
4. Действия над случайными событиями, вычисление вероятностей результатов действий.
5. Случайные величины, их виды. Закон распределения случайной величины
6. Ряд и функция распределения дискретной случайной величины.
7. Математическое ожидание дискретной случайной величины.
8. Дисперсия дискретной случайной величины.
Примеры решения задач
1) Имеется набор разноцветных шариков, среди которых 5 синих, 3 красных и 2 зеленых. Наугад извлекают 4 шарика. Найти вероятность того, что среди извлеченных шариков 2 синих, 1 красный и 1 зеленый.
Решение
Для определения вероятности случайного события будем использовать классическую формулу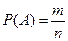 
, в которой n – число всех возможных исходов, m- число исходов, благоприятных появлению события. В задаче значения этих величин следует находить при помощи сочетаний.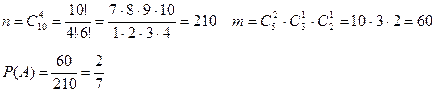 
2) Из карточек разрезной азбуки составлено слово «панорама». Карточки перемешали и наудачу по одной извлекают 5 карточек, выкладывая их в порядке извлечения. Найти вероятность того, что окажется составленным слово «роман».
Решение
В этой задаче можно воспользоваться произведением зависимых случайных событий
А – получение слова «роман»; В1 – извлечение первой карточки с буквой «р»;
В2 – извлечение второй карточки с буквой «о»; и т.д. Тогда А=В1 . В2 . В3 . В4 . В5
Р(А)=Р(В1) . Р(В2) . Р(В3) . Р(В4) . Р(В5)=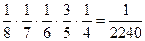 
3) В трех ящиках имеется по 6 одинаковых изделий, среди которых соответственно 2,
1, 3 бракованных. Наугад из каждого ящика извлекают по одному изделию. Найти вероятность того, что среди них окажутся два качественных и одно бракованное изделия.
Решение
Для решения задачи рассмотрим события: А – извлечение двух качественных и одного бракованного изделий, В1 – извлечение качественного изделия из первого ящика;
В2 – извлечение качественного изделия из второго ящика; В3– извлечение качественного изделия из третьего ящика; извлечение бракованного изделия для каждого ящика является событиями 
Составим событие А и вычислим его вероятность
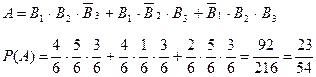
4) Вычислить математическое ожидание и дисперсию случайной величины, составить функцию распределения, начертить многоугольник распределения и график функции распределения. Имеется заданный ряд распределения дискретной случайной величины
| хi | -1 | ||
| pi | 0,5 | 0,3 | 0,2 |
Для вычисления математического ожидания воспользуемся формулой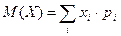 
Получим M(X)=(-1).0,5+2.0,3+6.0,2=1,3
Для вычисления дисперсии воспользуемся двумя соотношениями, одно из которых соответствует определению дисперсии, другое – ее свойству.
|
|
|
В примере получим: D(X)=(-1-1,3)2 . 0,5+(2-1,3)2 . 0,3+(6-1,3)2 . 0,2=7,21
M(X2)=(-1)2 . 0,5+22 . 0,3+62 . 0,2=8,9
D(X)= 8,9 – 1,32 =7,21 (значения должны совпадать)
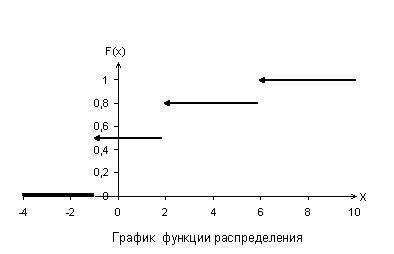
Для построения многоугольника распределения нужно на координатной плоскости построить точки (xi;pi) и последовательно их соединить отрезками.
Для построения функции распределения воспользуемся схемой:
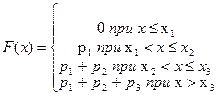
В примере получим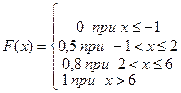 
Используя значения заданного примера получим графики:
РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ
Упражнение 1. Найти указанные пределы.
Решение:
1) 
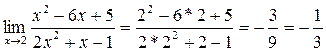
2) 
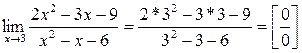
При подстановке вместо переменно х ее предельного значения 3 получается неопределенность вида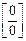 
. Для избавления от этого типа неопределенности в этом случае представим квадратные трехчлены числителя и знаменателя в виде произведения линейных множителей, воспользовавшись известной формулой 
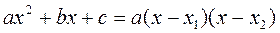, где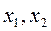 
- корни квадратного трехчлена 
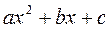. У нас 
, т.к. дискриминант квадратного трехчлена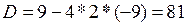 
, а следовательно, 
.
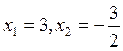Аналогично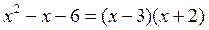 
.
Теперь условие примера можно переписать а другом виде и продолжить решение:
.
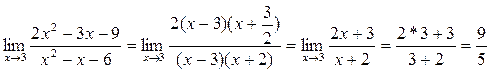3) 
.
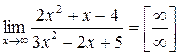Здесь сталкиваемся с неопределенностью вида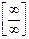 
, избавиться от которой можно вынесением за скобки в числителе и знаменателе дроби старшей степени переменной: 
.
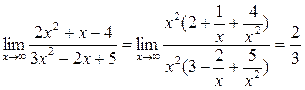4) 
.
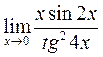В данном случае для освобождения от возникшей неопределенности вида будем использовать I замечательный предел и одно из его очевидных следствий:
.
Решение примера будет выглядеть следующим образом:
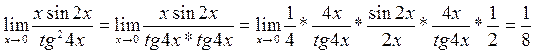
Упражнение 2. Найти производные, пользуясь правилами и формулами дифференцирования.
Решение:
Кроме формул дифференцирования нужно использовать правила дифференцирования (суммы, разности, произведения, частного).
Необходима и теорема о производной сложной функции:
если задана сложная функция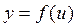 
, где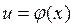 
, то есть 
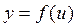; если каждая из функций и 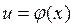дифференцируема по своему аргументу, то
.
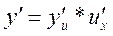1) 
, 
,
.
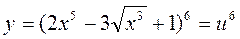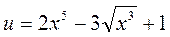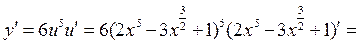
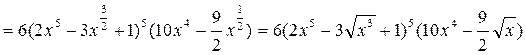2) 
,
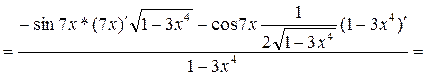
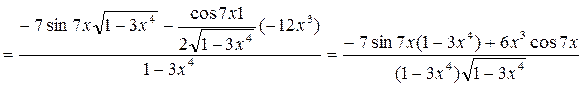
3) 
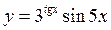
4) 
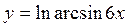
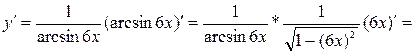
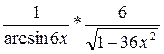
Упражнение 3. Исследовать функцию методами дифференциального исчисления и начертить график.
Исследование функции и построение графика рекомендуется проводить по следующей схеме:
1) найти область определения функции D(y);
2) найти точки экстремума функции и определить интервалы ее монотонности;
3) найти точки перегиба графика функции и определить интервалы выпуклости и вогнутости графика функции;
4) найти асимптоты графика функции;
5) построить график, используя результаты предыдущих исследований;
6) дополнительно найти наибольшее и наименьшее значения на отрезке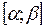 
.
Решение:
Дана функция: 
1) Областью определения данной функции являются все действительные значения аргумента х, то есть D(y): 
, а это значит, что функция непрерывна на всей числовой прямой и график ее не имеет вертикальных асимптот.
2) Исследуем функцию на экстремум и интервалы монотонности. С этой целью найдем ее производную и приравняем к нулю:
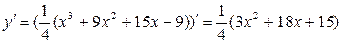
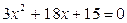
Решая полученное квадратное уравнение, делаем вывод о том, что функция имеет две критические точки I рода х1 = -5, х2 = -1. Разбиваем область определения этими точками на части и по изменению знака производной в них выявляем промежутки монотонности и наличие экстремума:
| x |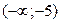 
| -5 | 
| -1 | 
|
| + | - | + | ||
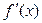
| & | max | ( | min | & |
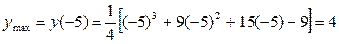
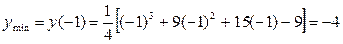
3) Определим точки перегиба графика функции и интервалы его выпуклости и вогнутости. Для этого найдем II производную заданной функции и приравняем ее к нулю:
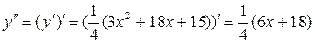
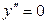, т.е.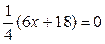 
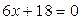
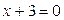
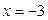
Итак, функция имеет одну критическую точку 2 рода 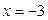. Разобьем область определения полученной точкой на части, в каждой из которой установим знак II производной:
| x |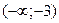 
| -3 |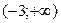 
|
| - | + | |
|
| 
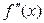
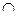
| т.п. |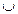 
|
Значение 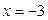является абсциссой точки перегиба графика функции, а ордината этой точки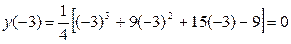 
4) Выясним наличие у графика заданной функции наклонных асимптот. Для определения параметров уравнения асимптоты 
воспользуемся формулами: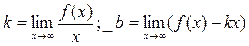 
.
Имеем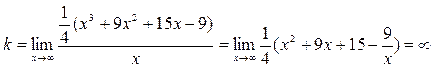 
.
Таким образом, у графика заданной функции наклонных асимптот нет.
5) 
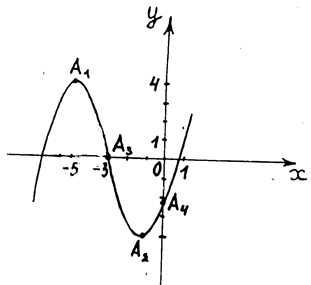Для построения графика в выбранной системе координат изобразим точки максимума А1(-5; 4), минимума А2(-1; -4), перегиба А3 (-3; 0) и точку пересечения графика с осью Оу А4 (0; 
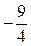). С учетом результатов предыдущих исследований построим кривую.
6) Найдем наибольшее и наименьшее значения заданной функции на отрезке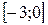 
. Для этого посчитаем значения функции на концах этого отрезка, в критических точках I рода, попавших на отрезок, и сравним результаты:
.
Очевидно, что 
.
Упражнение 5. Найти неопределенные интегралы
а) способом подстановки (методом замена переменной) 
, 
;
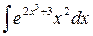б) применяя метод интегрирования по частям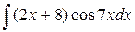 
, 
.
Решение:
а) : применим подстановку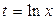 
. Тогда 
и 
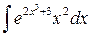: применим подстановку 
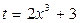. Тогда 
,
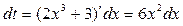, откуда 
б) 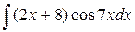: применим формулу интегрирования по частям 
.
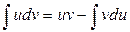Положим 
. Тогда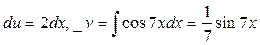 
.
Следовательно,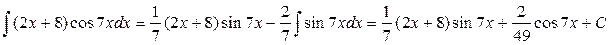 
.
: положим 
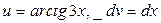. Тогда 
.
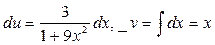Отсюда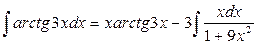 
. Применяя в последнем интеграле подстановку 
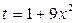, получаем 
, следовательно, 
.
Отсюда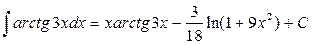 
.
Упражнение 6. В ычислить площадь плоской фигуры, ограниченную параболами.
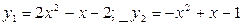
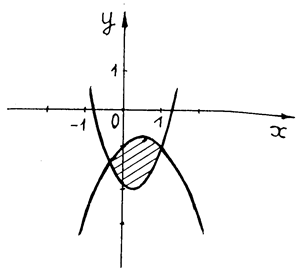Решение:
Найдем абсциссы точек пересечения заданных парабол. Для этого приравняем правые части их уравнений: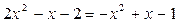 
.
Решаем полученное квадратное уравнение: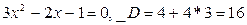 
.
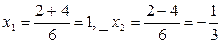Вычисление площади фигуры осуществляем по формул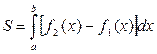е 
, где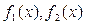 
- кривые, ограничивающие фигуру 
.
В нашем случае 
(кв. ед.)
Упражнение 7. Найти общее решение (общий интеграл) дифференциального уравнения I порядка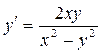 
.
Решение:
Правая часть уравнения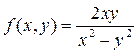 
обладает свойством 
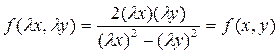. Поэтому заданное уравнение является однородным дифференциальным уравнением I порядка. Совершим замену 
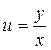, где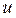 
- некоторая функция от аргумента х. Отсюда 
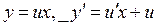. Исходное уравнение приобретает вид 
.
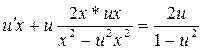Продолжаем преобразования: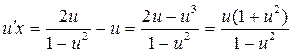 
; 
.
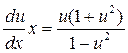Производим разделение переменных: 
.
После интегрирования обеих частей уравнения получаем
;
.
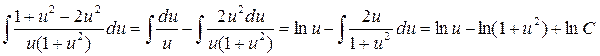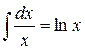Таким образом 
; 
.
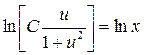Потенцируя, находим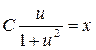 
или 
; 
.
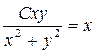Итак, общий интеграл исходного уравнения приобретает вид
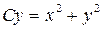, где С – произвольная постоянная.
Упражнение 8. Найти частное решение линейного однородного дифференциального уравнения II порядка с постоянными коэффициентами:
а) 
б)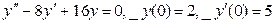 
в)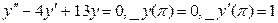 
Решение:
а) Для заданного дифференциального уравнения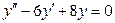 
составим соответствующее характеристическое уравнение 
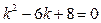по принципу: 
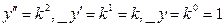. Решаем полученное квадратное уравнение и получаем два вещественных разных корня 
.
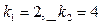Т.к.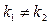 
, то общее решение данных уравнений записывается в виде 
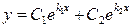. В нашем случае 
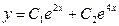, где 
- произвольные постоянные.
Отсюда 
, 
.
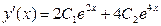Используя начальные условия 
: 
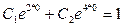, т.е. 
.
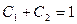Из того что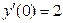 
следует 
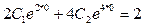, т.е. 
, 
.
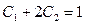Решая систему уравнений 
, получаем 
.
Теперь в наше общее решение 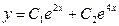подставим найденные значения . Частное решение исходного уравнения, удовлетворяющее заданным начальным условиям, приобретает вид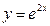 
.
б) Для заданного дифференциального уравнения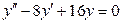 
составим соответствующее характеристическое уравнение 
по принципу: 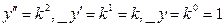. Решаем полученное квадратное уравнение и получаем два равных вещественных корня 
.
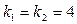Т.к. 
, то общее решение данных уравнений записывается в виде 
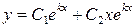. В нашем случае 
, где - произвольные постоянные.
Отсюда 
, 
.
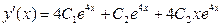Учитывая начальные условия, получаем систему уравнений для определения : 
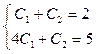. Решая систему, получаем 
.
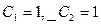Искомое частное решение имеет вид: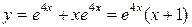 
в) Для заданного дифференциального уравнения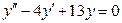 
составим соответствующее характеристическое уравнение 
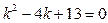. Решая это уравнение, убеждаем, что оно не имеет вещественных корней.
В этом случае общее решение соответствующего дифференциального уравнения записывается в ви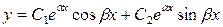де 
, где 
- коэффициенты характеристического уравнения).
У нас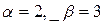 
поэтому общее решение заданного дифференциального уравнения имеет вид 
.
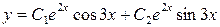Отсюда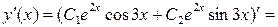 
.
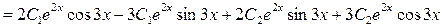Таким образом, для определения значений исходя из начальных условий, получаем систему уравнений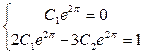 
,
решая которую имеем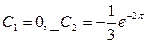 
.
Итак, искомое частное решение приобретает вид
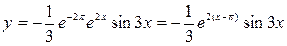
Упражнение 9. Дискретная случайная величина Х имеет только два возможных значения х1 и х2, причем х1 < х2. Найти закон распределения величины Х, если известно, что математическое ожидание М (х) = 1,4, дисперсия D (х) = 0,24 и вероятность р1 того, что Х примет значение х1, равна 0,6.
Решение:
Так как сумма вероятностей всех возможных значений Х равна 1, то вероятность p2 того, что Х примет значение х2, равна p2 = 1 - p1 = 1 – 0,6 = 0,4.
Напишем закон распределения Х:
| Х | х1 | х2 |
| p | 0,6 | 0,4 |
Для отыскания х1 и х2 составим два уравнения.
Для составления первого уравнения воспользуемся тем, что математическое ожидание
M(x) определяется по формуле M(x) = х1 р1 + х2 р2 + … + хn рn
В нашем случае: M(x) = х1 р1 + х2 р2
Учитывая, что по условию M(x) = 1,4, можем записать первое уравнение:
0,6х1 + 0,4х2 = 1,4.
Учитывая, что по условию D(x) = 0,24, пользуясь формулой D (х) = M (X2) – [M(X)]2, напишем второе уравнение:
0,6 х12 + 0,4 х22 - 1,42 = 0,24, или
0,6 х12 + 0,4 х22 = 2,2.
Решив полученную систему уравнений, найдем два решения:
х1 = 1, х2 = 2 и х1 = 1,8, х2 = 0,8.
По условию, х1 < х2, поэтому задаче удовлетворяет лишь первое решение.
Окончательно получим искомый закон распределения:
| Х | ||
| p | 0,6 | 0,4 |
Ряды Записать ряд по его заданному общему члену:
;
;
.
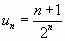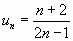Решение.
Полагая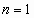 
, 
, 
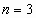,…, имеем бесконечную последовательность чисел:
, 
, 
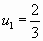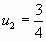. Сложив его члены, получим ряд
.
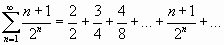Поступая так же, получим ряд
.
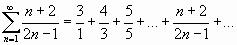Придавая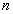 
значения 1,2,3,… и учитывая, что 
, 
, 
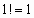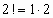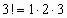,…, получим ряд
.
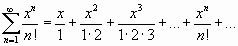Найти n- ый член ряда по его данным первым членам:
;
.
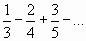Решение.
Знаменатели членов ряда, начиная с первого, являются четными числами; следовательно, n- ый член ряда имеет вид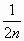 
.
Числители членов ряда образуют натуральный ряд чисел, а соответствующие им знаменатели – натуральный ряд чисел, а соответствующие им знаменатели – натуральный ряд чисел, начиная с 3. Знаки чередуются по закону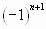 
или по закону 
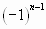. Значит, n- й член ряда имеет вид . 
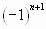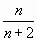или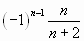 
.
Исследовать сходимость ряда, применяя необходимый признак сходимости и признак сравнения:
;
;
.
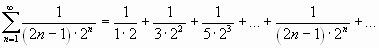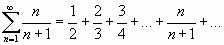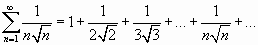Решение.
Находим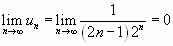 
.
Необходимый признак сходимости ряда выполняется, но для решени
|
|
|
