Динамика оснований и фундаментов

В предыдущих разделах книги были рассмотрены вопросы напряженного со­стояния и деформаций грунтов под влиянием ста­тических, т. е. не меняю­щихся во времени или весьма медленно ме­няющихся воздействий. Но как бу­дет пока­зано ниже, прочностные свойства грунтов (особенно дисперсных) и их несущая способность существенно изменяются под влиянием различного рода динами­ческих воздей­ствий, возбуждаемых динамическими нагрузками от неуравнове­шенных машин, движением транспорта, ветра и т. п.

Колебания от этих источников вибраций распространяются на значитель­ные расстоя­ния через грунт и передаются окружающим зданиям, сооружениям и наземным резервуарам, которые опираются на песчаные основания боль­шой площади. Под влиянием распространяющихся через грунт сотрясений не­редко уси­ливается развитие неравномерных осадок зданий и сооружений, а также де­форма­ций конструкций. Поэтому учет динамических нагрузок при проек­тиро­вании технологических объектов транспорта и хранения нефти и газа в на­стоящее время является обяза­тельным.

Давно уже установлено, что под влиянием вибраций сопротивление грунтов сдвигу снижается, однако в настоящее время о его природе и в особенности о количественных характеристиках имеется лишь при­ближенное представление.

Причина этого обстоятельства заключается, прежде всего, в том, что сниже­ние сопротивления грунтов сдвигу может зависеть от двух факторов, раздель­ные изучение которых представляют большое затруд­нение. Первый из них - изменение истинного коэффициента внутрен­него трения в величине сце­пления вследствие изменения физико-меха­нических свойств грунта под дейст­вием вибраций.

Имеющиеся экспе­риментальные данные показывают, что при сильных виб­рациях это из­менение может быть весьма значительным; в водонасыщенных песчаных грунтах при их расширении в процессе уплотнения под влиянием ви­браций наблюдается почти полное исчезновение внутреннего трения. Не столько значительным, но все же существенным может быть снижение коэф­фициента внутреннего трения и в сухих песках при их уплотне­нии, а также в пластичных глинистых грунтах. Однако при слабых ви­брациях изменения ис­тинного коэффициента внутреннего трения и ве­личины сцепления грунтов бы­вают небольшими, а в некоторых случаях вовсе не имеют места.

Вторым фактором является изменение напряженного состояния грунта при вибрациях. Если под влиянием вибраций периодически уменьшается нор­мальное составляющее давления на плоскость сдвига или возникают силы инерции, действующие в направлении статическо­го сдвигающего усилия, то, естественно, снижается и эффективное со­противление сдвигу, даже если коэф­фициент внутреннего трения и величина сцепления остаются совершенно не­изменными.

В результате анализа работ многих авторов в настоящее время можно счи­тать установленным, что изменение сопротивления грунтов сдвигу при пульси­рующих напряжениях одного знака происходит не за счет изменения истинного угла внутреннего трения, который остается таким же как при ста­тических воз­действиях, а в связи с изменением напряженного состояния под влиянием виб­раций. Другими словами, под воздействием вибраций происхо­дит изменение лишь аффективного угла внутреннего трения в смысле, при­данном этому поня­тию И.И.Блехманом и Г.Ю.Джа­нелидзе [5]. Однако, как показывают наблю­дения, даже тогда, когда вибрации слабые и сдвигающие усилия, передаваемые на образец грунта, не достигает предельного значения, деформации сдвига все же могут иметь место. В этом случае они протекают с весьма малой постоян­ной или слабозатухающей скоростью все время, пока образец подвергается вибрации и, накапливаясь, могут достигать ощутимых величин.

Следовательно, для достаточно сильно нагруженных фундаментов даже сравнительно небольшие динамические нагрузки или слабые сотрясения осно­вания могут явиться причиной возникновения дополнительных (ди­намиче­ских) осадок.

Этот вывод подтверждается данными натурных наблюдений за пове­дением зданий и инженерных сооружений, возведенных в непосредственной близости от тех или иных источников вибраций.

Особенно наглядным в этом отношении являются результаты наблюдений за неравномерными динамическими осадками стальных вертикальных цилин­дри­ческих резервуаров из-за колебаний грунта от движущего железнодорож­ного состава, а также зданий, расположенных вблизи городских магистралей с ин­тенсивным движением транспорта. По имеющимся данным, при расстоя­ниях 10-15 м от оси улицы ускоре­ния колебания грунта на обычных глубинах зало­жения фундаментов жилых и общественных зданий могут составить 15-20 см / сек², то есть достигать примерно 0,03g. Многолетние наблюдения за осадками таких зданий, проводившиеся как в нашей стране, так и за рубежом, показы­вает, что сотрясения указанной интенсивности приводят к до­полни­тельной осадке зданий даже тогда, когда возраст конструкций очень велик и статиче­ская осадка полностью стабилизировалась. Например, среднегодовая осадка не­скольких десятков зданий в Петрограде в период 1911-1927 г.г. со­ставила всего 0,3 мм/год, а за 1927-1953 г.г. с увеличением интенсивности движения транспорта на улицах возросла более чем в 7 раз и достигла 2,2 мм/год. При­чем, эти осадки носят неравномерный характер и вызываются не уплотнением толщи грунта основания, а образованием в ней малых пластиче­ских сдвигов.

Чтобы изучить механизм образования динамических осадок оснований, рас­смотрим сначала процесс распространения волн напряжений и деформаций в грунте от перечисленных выше источников вибрации. В настоящее время при исследовании волновых процессов в грунтах наибольшее применение находят следующие модели грун­та: идеально упругой среды (линейной и нелинейной), упругопластической среды (X. А. Рахматулина, С. С. Григоряна и др.), модели вязкопластической среды (Г. М. Ляхова) и нелинейной дилатационной модели (А. П. Синицына) и др.

Модель идеально упругой сплошной среды является наиболее простой моде­лью для исследования волновых процессов в грунтах как сплошных средах. Эту модель применяют при невысоких давлениях, например при сейсмических воздействиях (на некотором уда­лении от очага землетрясения), колебаниях от неуравновешенных машин железных и шоссейных дорог и т. п., она позволяет уяснить картину распространения волн в грунтах и их взаимодействие с пре­градами. Поэтому перейдем к рассмотрению именно этой модели грунта.

6.1. Распространение волн в грунтах при динамических воздействиях

Дифференциальные уравнения распространения волн в изотропной иде­ально упругой среде плотностью r можно получить из общих уравнений рав­новесия прямоугольного параллелепипеда с ребрами dx, dy, dz (рис.6.1), выде­ленного в произвольной точке упругой среды.

 

 

Рис.6.1. Напряжения на гранях бесконечно малого параллелепипеда упругой среды

С этой целью воспользуемся уравнениями равновесия этого элемента теории упругости [12], записанными в перемещениях. Усилия, входящие в эти уравне­ния, приравняем нулю и добавим члены, содержащие инерционные силы.

Тогда дифференциальные уравнения перемещения волн в упругой среде при­мут вид:

(6.1)

где: 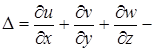объёмная деформация;

оператор Лапласа второго порядка;

E и G – модули упругости и сдвига упругой среды соответственно;

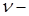коэффициент Пуассона;

u, v, w – перемещения элементов упругой среды соответственно вдоль коорди­натных осей 0x, 0y, 0z (рис.6.1).

Если предположить, что перемещения происходят только вдоль направле­ния оси 0x, то u = u(x,t); v = w = 0.

В этом случае

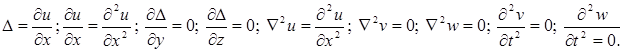
Если подставить полученные значения в систему дифференциальных урав­нений (6.1), то второе и третье уравнения удовлетворяются тождественно, а первое принимает вид:

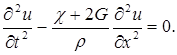(6.2)

Обозначим

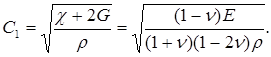(6.3)

Здесь С₁ представляет собой скорость распространения деформаций в упру­гой среде.

Решение дифференциального уравнения (6.2) можно представить в следую­щем виде:

(6.4)

где: А – амплитуда колебания, зависящая от интенсивности внешнего воз­действия и равная наибольшему перемещению каждой точки в упругой среде;

l₁ – длина продольной волны (расстояние между точками среды с одинако­выми перемещениями в один и тот же момент времени).

Период колебания равен:

(6.5)

Из соотношения (6.3) видно, что скорость распространения волн расшире­ния зависит только от упругих свойств грунта.

Рассмотрим теперь распространение поперечных волн (волн искажения) в упругой среде. В этом случае в точках упругой среды, расположенной на оси 0х, возможны только поперечные перемещения, параллельные оси 0z (рис.6.1), поэтому w= w(x,t); v = u = 0.

Кроме того:

После подстановки этих величин в систему дифференциальных уравнений (6.1) первые два уравнения обращаются в тождество, а третье уравнение при­нимает вид:

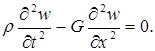(6.6)

В этом случае скорость поперечных волн равна:

(6.7)

а соотношение 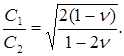(6.8)

С учетом численных значений коэффициента Пуассона грунтов из соотно­шения (6.8) следует, что скорость поперечных волн всегда меньше скорости продольных волн. То есть в упругой среде продольные волны опережают попе­речные. Это явление наблюдается при землетрясениях. На сейсмических стан­циях судят о расстояниях от эпицентра землетрясения по величине запаз­дыва­ния поперечных волн в сравнении с продольными.

Численные значения С₁ и С₂ для некоторых видов грунтов представлены в таблице 6.1.

Таблица 6.1.

№	Тип грунта	С1, см/сек	С2, см/сек
	Песок	слабовлажный	200-500	120-150
водонасыщенный	500-1000	120-150
	Глины и суглинки	твердые	1100-1500	400-600
пластичные	300-1000	150-400
	Лёсс естественной влажности	600-800	130-160
	Гравелисто-песчаный грунт	400-1000	150-200

 

Для поперечных колебаний решение дифференциального уравнения (6.6) имеет вид:

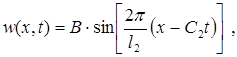(6.9)

где B - амплитуда поперечных колебаний,

l₂ = T₂ × C₂ - длина поперечной волны,

T ₂ - период колебания.

Поперечные колебания сопровождаются сдвигами и искажениями углов, по­этому они и называются волнами искажения.

В однородной упругой среде продольные и поперечные волны распростра­няются независимо друг от друга. В зависимости от характера начального смещения среды, вызывающего колебания, могут возникнуть либо оба указан­ных вида волн, либо один вид.

На поверхности среды возможно появление волн различного типа, прони­кающих внутрь среды лишь на небольшую глубину (порядка длины волны). Так как все источники возбуждения колебания расположены фактически на по­верхности промышленных территорий (или близко к ним), изучение по­верхно­стных волн представляет большой интерес при решении рассматривае­мой за­дачи. Подробное ис­следование динамики движения поверхностных волн (волн Релея) в упругой среде представлено в работе [13].

Поверхностные волны, распространяясь лишь в двух направлениях, на срав­нительно небольшом расстоянии от источника приобретают непрерывно воз­растающее преобладание над продольными и поперечными. Поэтому, при ре­шении практических задач динамики оснований обычно принимают во внима­ние именно поверхностные волны.

Скорость С₃ распространения поверхностных волн в однородной среде не­сколько меньше скорости поперечных волн:

С₃ = nС₂. (6.10)

Коэффициент n определяется путем решения уравнения:

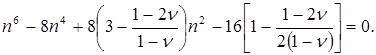(6.11)

Например, при численном значении коэффициента Пуассона n =0,25 полу­чим:

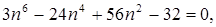
или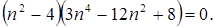

Из трех корней этого уравнения следует выби­рать наименьшее значение n² (иначе теряется физический смысл решае­мой задачи). Поэтому 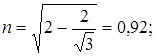а С₃ = 0,92С₂.; при n =0,5 n = 0,95 и С₃ = 0,95С₂.

Периоды колебаний грунта, вызываемых поверхностными волнами, распро­страняющимися от фундаментов машин с установившимся движе­нием, равны периодам возмущающих сил, возникающих при работе машин. Что касается колебаний грунта, наблюдающихся при действии на фун­дамент ударных или иных нагрузок типа импульса, то, как показали экспериментальные исследова­ния И.Р.Свинкина [18], Я.Н.Смоликова [19] и других авторов, периоды этих колебаний весьма близки к периодам собственных колебаний фундамента - ис­точника, возникающих под действием ударов.

Таким образом, если известны характеристики упругости среды, в каждом случае нетрудно приближенно вычислить скорость распростра­нения поверхно­стных волн, а для источников подвергающихся действию ударных нагрузок - также и периоды Т колебаний грунта. Зная вели­чины С₃ и Т для различных случаев можно найти длину рас­пространяющихся волн, численно равную про­изведению С₃×Т.

Скорость распространения поверхностных волн в грунтах четвер­тичных от­ложений, на которых возведено подавляющее большинство промышленных предприятий, обычно колеблются в пределах от 75 м/с до 300 м/с, а соответст­вующие этим цифрам длины волн в пре­делах от 2 до 200 м (в зави­симости от частоты). Так, если длины волн, распространяющихся от фунда­ментов низко­частотных машин (компрессоров, лесопильных дробилок и др.) весьма значи­тельны и достигают несколько десятков (и иногда и сотен) мет­ров, то для вы­сокочастотных агрегатов они значительно меньше. Например, от фундаментов под турбоагрегаты при скорости вращения вала 1500-3000 об/мин распростра­няются волны длиной не более 10-12 м. Длины волн, рас­пространяющихся от фундаментов под молоты, собственные частоты, которых обычно близки (800-1200 кол/мин), варьируют в пределах от 5 до 20 м.

Для предупреждения неравномерных осадок оснований, сложенных из не­связных грунтов, большое значение имеет вопрос выбора безопасного расстоя­ния между источником вибрации и основанием, при котором не возникнет про­цесс виброползучести грунта основания.

Определение амплитуд поверх­ностных волн на сравнительно больших рас­стояниях от источника колебаний можно производить по формуле Д.Д. Бар­кана [1]:

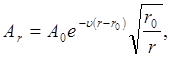(6.12)

где А_r и A₀ - амплитуды колебаний грунта на расстоянии r и r₀ от источника; ex - коэффициент затухания колебаний, м ^-1.

На основании опытов, произведенных Я. Н. Смоляковым, в прак­тических целях для различных грунтов можно пользоваться следую­щими значениями коэффициента затухания колебаний :

мелкозернистые песчаные, супесчаные и суг­линистые грунты, насыщенные во­дой = 0,03 -0,04 м ^{– 1};

пески средние и крупнозернистые (независи­мо от влажности); влажные глины и суглинки =0,04 - 0,06 м ^{– 1};

суглинки и супеси (сухие и слабовлажные) = 0,06 - 0,10 м ^–1.

Существенное значение имеют результаты экспериментального изучения из­менений амплитуд поверхностных волн по глубине. Так, оказалось, что на ма­лых глубинах, не превышающих 0,2 - 0,3 длины волны, амплитуды колеба­ний уменьшаются сравнительно незначи­тельно.

О характере затухания поверхностных волн по глубине можно судить по графику Д. Д. Баркана (рис.6.2), который построен по данным измерения вер­тикальных колебаний, вызываемых работой копра.

Рис.6.2. Изменение амплитуд колебаний грунта под фундаментом

Следует иметь в виду, что в непосредственной близости к фун­даменту (ис­точнику волн) характер изменения амплитуд с глубиной будет несколько иным (рис.6.3). Рассматривая этот график, можно убедиться, что не следует за­клады­вать фундаменты машин (например, насосных или компрессорных це­хов) глубже, чем смежные фундаменты зда­ний или сооружений; часто целесо­образ­нее на­значать глубину заложения фундаментов под машины (на основа­нии опытов, произведенных Я. Н. Смоликовым) меньше, чем глубина заложе­ния фундамен­тов близлежащих зданий.

Некоторые задачи динамики дисперсных грунтов принципиально не могут быть решены в рамках модели упругой среды. Так, например, решение задачи о распространении плоской волны приводит к отсут­ствию угасания и измене­ния профиля волны с расстоянием, что про­тиворечит опытным данным.

Более сложной является модель нелинейно упругой среды, в которой зависи­мость между напряжениями и деформациями нелинейна, но одинакова при росте и снижении нагрузки.

 

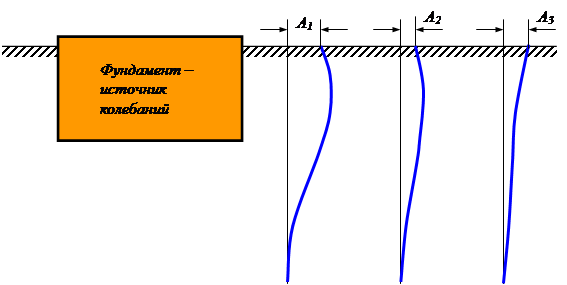Рис.6.3.Изменение амплитуд колебаний грунта на различном расстоянии от фундамента

Но формула Д.Д.Баркана (6.12) не учитывает свойства грунтов строительной площадки, геометрической формы фундамента – источника колебаний, вида и частотной характеристики динамического воздействия на фундамент. Как показывают данные натурных наблюдений, расчет по этой формуле приводит к завышенным значениям амплитуд колебаний.

Наиболее точные результаты дает метод оснований на анализе эксперимен­тальных и натурных исследованиях, выполненных О.А.Савиновым, Я.Д.Гиль-зельбергом, М.И.Забылиным и В.В.Игольниковым, В.А.Ильичевым и В.Г.Тарановым, А.А.Саниковым, Э.И. Дасовым и другими.

В основу метода положены результаты теоретического исследования рас­пространения волн в упругом полупространстве при сосредоточен­ных горизон­тальном, вертикальном и моментном воздействиях, выпол­ненного Я.Д.Гиль-зельбергом и К.И.Огурцовым [6, 7]. В ходе этого исследования были полу­чены формулы, описывающие поля смещения по­верхности полупро­странства от ка­ждого из указанных воздействий, изменяющихся во времени по линей­ному за­кону. Далее, пользуясь мето­дом наложения, авторы осуществили пере­ход к им­пульсному (треуголь­ному) и синусоидальному воздействиям, а затем построили для таких источников сеймограммы на различных расстоя­ниях от них.

Полученные Я.Д.Гильзельбергом и К. И. Огурцовым графики зависи­мости максимальных смещений поверхности полупространства от относительного расстояния r/s (где r - расстояние от оси источни­ка; s - полуразмер его по­дошвы) при (вертикальное воздействие) представлены на рис. 6.4 – 6.6. Символом W обозначена вертикальная, U_r и U_v - соответственно ради­альная и тангенсальная составляющая максимального смещения по­верх­ности грунта, выраженные в процентах от величины максимально­го смещения грунта непо­средственно рядом с фундаментом-источником колебаний в рас­сматри­ваемом направлении.

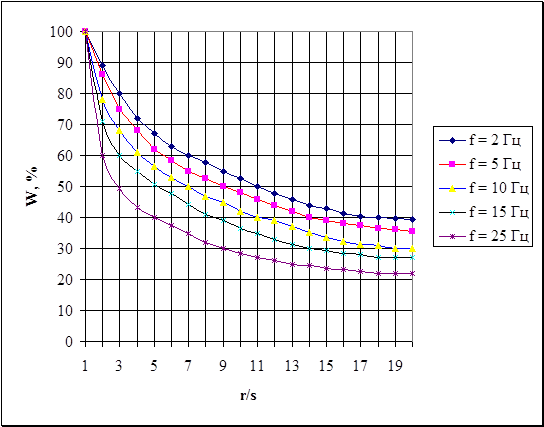
Рис.6.4. Графики зависимости W = f(r/s)

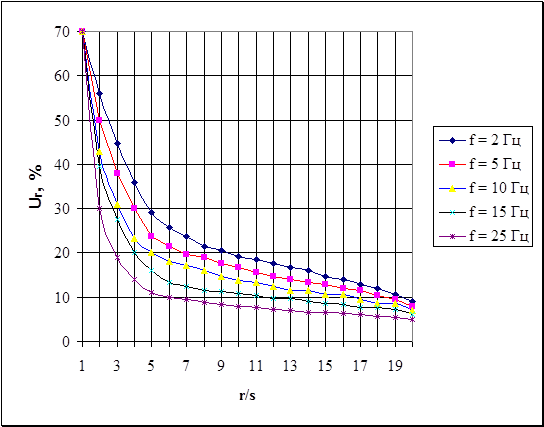
Рис.6.5. Графики зависимости U_r = f(r/s)

 

Рис.6.6. Графики зависимости U_v = f(r/s)

Из графиков видно, что эти смещения зависят от частоты возму­щения f и от параметра Как оказалось, около фундаментов промышленных устано­вок можно выде­лить зону, в которой сказываются особенности прило­жения динамической нагрузки на грунт. Главный признак этой зоны - форма волнового фронта, которая из прямо­угольной, соответствующей форме по­дошвы источника, вырождается с расстоянием, проходя через эллип­тическую в кольцевую, такую же, как у сосредоточенного источника.

При низкочастотных возмущениях, характерных для промышленной сейс­мики, величины максимальных Релеевских или квазистатических смещений, вызванных гармоническим и импульсным воздействиями, близки друг к другу, что в принципе позволяет распространить графики, помещенные на рис.6.4-6.6 на все типы промышленных установок.

Эти выводы были подтверждены путем экспериментальных исследований в полигонных и натурных условиях. Одновременно были проанализиро­ваны дан-ные экспериментов, проведенных другими авторами. Цель ра­боты заклю­чалась в проверке результатов теоретических исследований и в получении до­полни­тель­ных данных, необходимых для учета поглощения энергии на пути распро­стра­нения волн, выявления местных особеннос­тей передачи колебаний от фун­да­мента грунтовому массиву и др.

В соответствии с этим в составе обследован­ных объектов имелись ис­точ­ники как с импульсным, так и гармоническим ха­рактером воздей­ствия.

Основные результаты экспериментальных исследований сводятся к следую­щему:

- всесторонне проверен и подтвержден основной вывод о том, что каждому сочетанию инженерно-геологических условий промплощадки и особенностям приложения динамической нагрузки соответствует своя кривая затухания коле­баний с расстоянием от источника;

- подтверждена правильность вывода исследователей о на­личии перепада амплитуд колебаний между фундаментом машины (источ­ником колебаний) и грунтом рядом с ним. Установлено, что коэффи­циент перепада К_П, равный от­ношению амплитуды колебаний грунта рядом с фундаментом к амплитуде ко­лебаний фундамента, зависят от соотношения между частотами собственных и вынужденных колебаний источника и от характеристик упругости грунтов ос­нования.

В дорезонанской области всегда К_П < 1. В области первого ре­зонанса вели­чина К_П достигает минимума, а в зарезонанской области возрастает и при неко­торых условиях может быть больше единицы. Для низкочастотных не­уравно­вешенных машин величину К_П можно опре­делить по графику (рис. 6.7).

Рис.6.7.Функциональная зависимость К_П = f (n₀ = C₂ /C₁)

Подтвержден вывод о существовании около фундамента источника волн "ближней" зоны, в которой необходимо учитывать особенности приложения нагрузки. Радиус r_з площади "ближней" зоны может с достаточной для практи­ческих целей точностью определяться по фор­муле [17]:

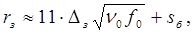(6.13)

где: D_з – разница в длинах сторон подошвы фундамента – источника колеба­ний;

f₀ – безразмерная величина, численно равная частоте возмущения f, Гц;

s_б – полуразмер большей стороны подошвы фундамента.

Натурные измерения, проведенные на 30 промышленных площадках с раз­личными грунтовыми условиями, показали [17], что наиболее точно характер за­тухания колебаний, вызванных работой промышленных установок, выража­ется формулой:

(6.14)

где: A₀ и A_r – амплитуда вертикальных (горизонтальных) колебаний грунта соответственно под подошвой фундамента и на расстоянии r от центра пло­щади его;

x - относительная амплитуда колебаний, определяемая по соответствующим графикам (рис. 6.4 и 6.5);

h₀ – параметр, учитывающий в «ближней» зоне не только неупругие свой­ства грунта, но и особенности приложения динамической нагрузки.

В интервале s £ r £ r_з 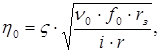(6.15)

а при r > r_з (6.16)

где: V - безразмерный коэффициент, принимаемый для вертикальных коле­баний равным 0,06, а для горизонтальных – 0,043;

i – отношение большей стороны подошвы фундамента (источника вибра­ций) к меньшей.

Учитывая, что часто при проектировании отсутствуют сведения о скоростях продольных и поперечных волн в грунтах, Я.Д. Гимзельберг предложил для определения параметра следующую эмпирическую формулу [7]:

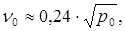(6.17)

где p₀ – условное расчетное давление на грунт, кгс/см ² (СНИП II.15-74).

6.2.Влияние вибрационных нагрузок на прочностные и деформационные свойства грунтовых оснований

Динамические воздействия как слабые, возникающие вследствие движения неуравновешенных частей машин (вибрации, колебания и пр.), так и сильные - кратковременные однократные и многократные (удары, импульсы большой силы, взрывы и т. п.), существенно ска­зываются на свойствах несвязных (сы­пучих) грунтов и несколько меньше грунтов связных (глинистых). Распростра­няясь в упругой грунтовой среде с большой скоростью от источников вибра­ций, поверхностные волны достигают оснований, на которые опираются фун­даменты различных сооружений нефтяной и газовой промышленности. Вибра­ции вызывают уменьшение трения между частицами грун­тов оснований и об­щее уменьшение их сопротивления сдвигу, (что снижает несущую способ­ность грунтов); импульсные воздействия средней величины (при ускорениях, мень­ших ускорения силы тяжести) вы­зывают осадки и просадки, а импульсы значи­тельной величины - разрушение структуры грунтов и потерю их прочно­сти.

Рассмотрим, как изменяются прочностные свойства грунтовых оснований при динамических воздействиях.

Уменьшение сопротивления сдвигу при вибрациях в грунтах яв­ляется ос­нов­ным фактором, влияющим на прочностные свойства грунтов.

Еще в 30-х годах проф. Г. И. Покровским было установлено, что коэффи­ци­ент внутреннего трения грунтов зависит от энергии колебаний, уменьшаясь с ее увеличением, стремясь, однако, к неко­торому пределу. Для грунтов же связ­ных влияние вибрации на со­противление сдвигу будет тем меньше, чем больше сцепление грунта.

Согласно опытам В. А. Ершова и Се-Дин-И (ЛИСИ, 1962), при вибрациях наб­людалось постепенное снижение сопротивления песчаных грунтов сдвигу (рис. 6.8), которое можно описать эмпири­ческой зависимостью

(6.18)

где: t - сопротивление сдвигу при 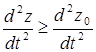(причем 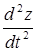- ускорение ко­ле­баний при данной возмущающей силе, a - начальное ускорение, до вели­чины которого не происходит еще изменений сопротивления сдвигу);

t₀ - сопротивление сдвигу при статических нагрузках;

V - постоянный коэффициент, равный 0,003 сек²/см для мелкозернистого и 0,0025 сек²/см для среднезернистого песка.

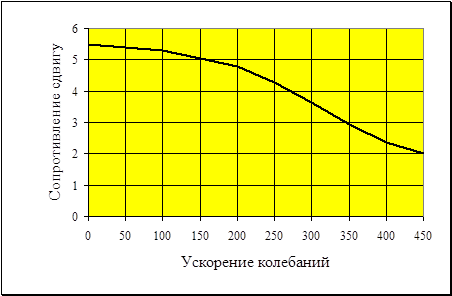
Рис.6.8. Зависимость сопротивления грунта сдвигу (Н/см²) от ускорения ко­лебаний (см/сек²)

На основании опытов было также установлено, что начальное ускорение (когда при вибрациях еще не преодолеваются структур­ные связи в точ­ках контакта грун­товых частиц и не снижается соп­ротивление грунта сдвигу) линейно зависит от величины внешнего дав­ления на грунт, возрастая с его уве­личением.

При определенной частоте ко­лебаний трение в грунтах (особенно у несвяз­ных) может настолько уме­ньшиться, что грунты приобретают свойства вязкой жидкости (вибро­вязкость) с внутренним трением, близким к нулю, и ничтож­ной не­сущей способностью. Проф. Д.Д. Баркан демонстрировал свойства виб­ровязкости песчаных грунтов на следующем опыте: он помещал на дно стек­лянного сосуда дробинку и засыпал ее песком. Удельный вес этой дробинки был ниже объёмного веса песка. В процессе вибраций с определенной часто­той колебаний дробинка в сосуде медленно всплывала через толщу песка на его поверхность. Если же на песчаную поверхность поместить дробинку с удельным весом большим, чем объёмный вес песка, например, свинцовую, то при вибрациях сосуда с песчаным грунтом, свинцовая дробинка окажется на дне сосуда.

Эта особенность действия вибра­ций на сыпучие грунты была использована Д.Д. Барканом при раз­работке виброметода – быстрого погружения (забивки) с помощью вибраций шпунтов, свай и опор-оболочек в несвязные грунты на глубину до нескольких десятков метров [2]. Скорость погружения конструкций в грунт виброметодом зависит от час­тоты применяемых вибраций, величины возмущающих сил и свойств вибровяз­кости грунтов.

Вибровязкость грунтов может быть охарактеризована некоторым коэффици­ентом вибровязкости, величина которого различна для различных грунтов и за­висит от относительного ускорения колебаний, что может быть описано зави­симостью 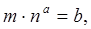(6.19)

где m - коэффициент вибровязкости, H×сек/см²; п -отношение ускорения ко­лебаний к ускорению силы тяжести; a, b - эмпиричес­кие коэффициенты.

Опыты Д. Д. Баркана показали, что величина коэффициента вибровязкости зависит от физического состояния грунтов и особенно от их влажности.

На рис. 6.9 приведена кривая зависимости коэффициента вибро­вязкости мелкозернистого песка от влажности, из которой видно, что наименьшая вели­чина коэффициента вибровязкости наблюдается у сухих и полностью водона­сыщенных песков и при некоторой величи­не влажности (в данном случае 14%) имеет место максимум вибровязкости.

Подобные же результаты были по­лучены и для слабых глинистых грун­тов, супесей и суглин­ков. Приведенные данные показывают, что наиболее успешно погружение шпунтов, свай и т. п. конструкций будет в случае песчаных грун­тов - сухих и водонасыщенных. Производ­ственные испытания [17] показы­вают, что скорость погружения в грунт свай с помощью высокочастотных виб­рато­ров (особенно с подрессоренной на­грузкой) достигает нескольких мет­ров в ми­нуту.

Рис.6.9. Зависимость коэффициента вибровязкости песка от влажности

Как пример на рис. 6.10 приве­ден график погружения вибрирова­нием метал­лического шпунта в песчаные грунты на глубину около 13 м, на что по­требова­лось менее 6 мин времени [17].

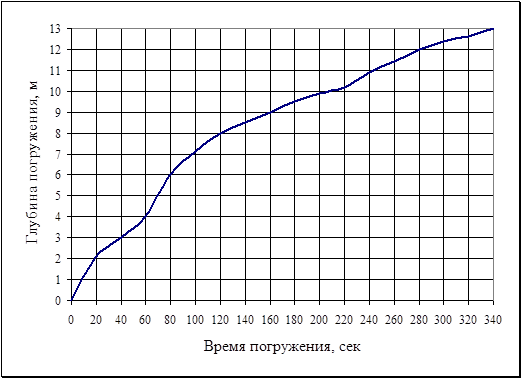
Рис.6.10. График вибропогружения металлического шпунта в песчаный грунт

В настоящее время виброметод находит широкое применение в фундамен-тостроении, при прокладке магистральных трубопроводов в грунтах под ис­кус­ственными и естественными препятствиями, при установке свай и анкер­ных устройств и в других слу­чаях погружения трубчатых конструкций в грунт.

Виброуплотнение. Под действием вибраций рыхлые отложения грунтов, особенно не обладающие сцеплением, могут давать значи­тельные осадки, обу­словленные изменением пористости грунтов в про­цессе их вибрирования.

Иногда осадки оснований соседних с работающими машинами фундаментов достигают нескольких десятков сантиметров, что влечет за собой недопусти­мые деформации промышленных объектов.

По данным Д. Д. Баркана, на одном заводе от вибраций, вызванных работой кузнечного молота (с весом падающего молота в 4,5 тc), возникли настолько значитель­ные осадки грунтов основания соседнего кирпичного здания, распо­ложенного на расстоянии 6 м от фундамента молота, что постепенно привели здание к разрушению [1].

Как показывают соответствующие исследования, между коэффи­циентом по­ристости грунтов (изменения которого и обусловливают осадки оснований) и ускорением колебаний существует зависимость, подобная компрессионной за­висимости, называемая виброкомпресси­онной кривой грунтов (рис.6.11).

Полученные О.В. Савиновым численные значения коэффициента динамиче­ского уплотнения песчаных грунтов при вибрационных воздействиях, пред­ставлены в таблице 6.2 [17].

Таблица 6.2

№	Тип грунта	J
	Крупнозернистые пески	0,55 – 0,80
	Среднезернистые пески	0,58 - 0,60
	Мелкозернистые пески	0,80 - 0,82
	Шлак	0,40 - 0,50

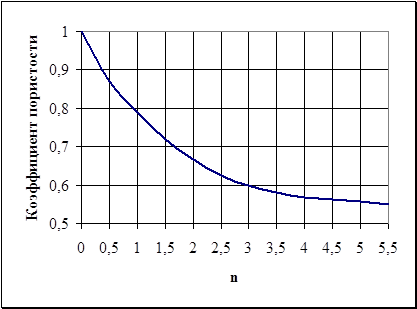
Рис.6.11. Зависимость коэффициента пористости песка e от отношения n ус­корения колебаний к ускорению силы тяжести

Функциональные зависимости у плотнения сухого среднезернистого песка представлены на рис. 6.12.

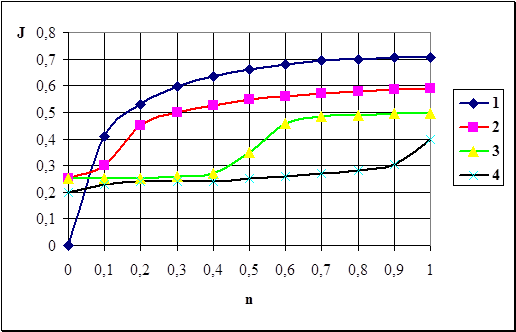
Рис.6.12. Кривые уплотнения сухого среднезернистого песка в зависимости от параметра n и интенсивности внешней нагрузки: 1 – р = 0; 2 - р = 4 Н/см²; 3 - р = 8 Н/см²; 4 - р = 10 Н/см².

На этих графиках по оси абсцисс отложена величина относительного уско-рения грунта n, а по оси ординат величина коэффициента динамического уплотнения:

(6.20)

где: e_д – динамический коэффициент пористости, соответствующий вибро-уплотнению грунта при действии внешней нагрузки;

e_max и e_min максимальное и минимальное значения коэффициентов пори­сто­сти в самом плотном и самом рыхлом состояниях песка без пригрузки.

Из рассмотрения результатов опытов по виброуплотнению грун­тов можно сделать следующие выводы.

1. При отсутствии внешней нагрузки (р = 0) уплотнение сыпу­чих грунтов начинается при любых слабых вибрациях и всегда завер­шается уплотнением, близким к полному (J» 1), причем это уплот­нение достигается для сухих пес­ков при ускорении вибраций от 0,2 до 1,2 g, для водонасыщенных от 0,5 до 2g и для влаж­ных - при 2g.

2. При действии внешней нагрузки (р ¹ 0) уплотнения грунтов практически не воз­никает лишь до некоторой критической величины уско­рения 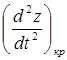; при большей же величине ускорения [для пес­ков больше (0,1 - 0,4)g ] имеет ме­сто виброуплотнение, кото­рое при дальнейшем увели­чении ускорения стабили­зи­руется до некоторой пористо­сти e_д, соответствующей коэффициенту динами­ческого уплотнения J.

Опыты профессоров А. Казагранде, Т. Сида и О. Олсона на одноосное, трех­осное сжатие и сдвиг глинистых грунтов показали, что их динамическая проч­ность R_д (при времени нагружения 0,02 сек.) гораздо больше статичес­кой R_ст , причем для относительно слабых глин R_д» 2 R_ст и для плот­ных глин R_д» 1,5 R_ст.

Сопротивление сдвигу глинистых грунтов в условиях закрытой системы также возрастает с увеличением скорости нагружения до 1,5 - 2,5 раз по срав­нению с сопротив­лением сдвигу при стати­ческой нагрузке.

Сравнивая прочность грунтов при кратковремен­ных (но неразрушающих) импульсах с прочностью при длительных вибрациях, можно придти к заклю­чению, что эти два вида динамиче­ских воздействий сказы­ваются противопо­ложно на механических свойствах грунтов - сопротивление грунтов при крат­ковремен­ных импульсах значитель­но больше, чем сопротивле­ние их при дли­тельно действующей виб­рации.