Главная | Обратная связь | Поможем написать вашу работу!

Расчёт на изгиб лопатки, связанной бандажом

Исходные данные те же, что и при расчёте лопатки без бандажа

Таблица№2

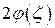
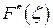
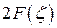
							*10^-7
	0,43
0,1	0,43	0,1	0,01	0,81	0,0905	0,009	0,0045	0,02
0,2	0,43	0,2	0,04	0,64	0,163	0,034	0,0170	0,1
0,3	0,43	0,3	0,09	0,49	0,2195	0,072	0,036	0,14
0,4	0,43	0,4	0,16	0,36	0,262	0,121	0,060	0,24
0,5	0,43	0,5	0,25	0,25	0,293	0,176	0,088	0,35
0,6	0,43	0,6	0,36	0,16	0,313	0,237	0,118	0,47
0,7	0,43	0,7	0,49	0,09	0,326	0,301	0,150	0,60
0,8	0,43	0,8	0,64	0,04	0,332	0,367	0,183	0,73
0,9	0,43	0,9	0,81	0,01	0,334	0,434	0,217	0,87
	0,43				0,335	0,501	0,250

Рис. 4. Вспомогательные кривые к расчету пакета лопаток на изгиб

Вычисляем величины:

где - относительная координата, .

Так как лопатка постоянного сечения, то при , следовательно .

Вносим значения в табл.1а.

Вычисляем интегралы:

Для этого по ординатам кривой , имеющимся в таблице 1а,вычисляем площади под этой кривой. Ординаты кривой вычислены для абсцисс 0,1;0,2;0,3…

Ординаты кривой для абсциссы 0,1 равна площади трапеции Oabc, средняя линия de (см. рис.3а.) которой равна . Поэтому площадь Oabc = 0,1·de = 0,1 .

Для абсциссы 0,2 ордината кривой равна площади Oafg=Oabc+cbfg.

Последняя площадь равна cbfg=0,1 .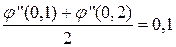

Площадь Oafg = 0,1+0,1=0,2 и т.д.

Для построения кривой поступаем аналогично. Для абсциссы 0,1 площадь под участком кривой равна . Для удобства находим двойную величину ординаты :

Для абсциссы 0,2:

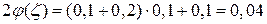Так же находятся величины 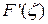и .Из таблицы 1а находим:

; .

Определяем коэффициент :

Изгибающий момент в корневом сечении лопатки:

По сравнению с лопаткой без бандажа этот момент снизился на

Напряжение изгиба в корневом сечении:

Для построения упругой линии лопатки при изгибе вычисляем по формуле прогибы лопатки в разных сечениях:

Рис. 5. Упругая линия лопатки при изгибе

Расчет вибрационной надежности облопачивания

Минимальная собственная частота единичной вращающейся лопатки с бандажом:

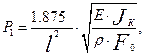
где плотность материала лопатки; - момент инерции сечения лопатки; F₀ =0,000207 м² - площадь поперечного сечения лопатки; - высота лопатки; модуль упругости, – число лопаток в пакете.

Тогда,

Собственная частота пакета лопаток:

Определим коэффициенты:

Гибкость лопатки:

По рис. 5.11 [3] получаем

Определим влияние вращения на частоту колебаний по тону А₀.

Определим влияние вращения на частоту колебаний по тону .

Динамическая частота на расчетном режиме:

где .

Частота колебаний на расчетном режиме (в Гц):

Рис. 6. Диаграмма Кэмпбелла.

Абсциссы точек пересечения лучей кратности с кривой частоты f_дколебаний начинаются от рабочей >15% для k=2, >8% для k=3, >6% для k=4, >5% для k=5, >3% для k=6, следовательно, лопатка вибронадежна.

Расчёт на прочность диска последней ступени

Исходные данные: n = 3000 об/мин, R =0,884 м, r_о = 0,1312 м,

r₁= r_в = 0,2361 м, r₂ = 0,46898 м, у₁= 0,0803 м, у_в = 0,2049 м, у₂= 0,05145 м,

s_r₀ = -5 МПа. Материал: ст. 35ХМ ρ = 7750 кг/м³.

Рисунок 8 – Диск последней ступени

Центробежная нагрузка на внешнем радиусе полотна:

где С _Л – центробежная сила облапачивания;

С_об – центробежная сила обода диска;

k – коэффициент, учитывающий разгружающее действие обода, k=2/3 для Т –образных и грибовидных хвостовиков, k=1,0 – для дисков с осевой завязкой хвостовиков лопаток, а так же дисков последних ступеней, имеющих большие значения внешнего радиуса.

, где ; =1,143/0,0831=13,755;

u_ср= π·d_ср·n/60 = π ·1,143·3000/60 = 179,542 м/с;

z = 97шт.; F_к = 0,000122 м²;

Материал лопаток: 20Х13 с плотностью ρ = 7750 кг/м³;

Центробежная сила обода диска:

где h = 0,05545 м; b₁=0,071 м; r_об = 0,52465 м.

Центробежная сила бандажа:

где

Тогда

1. Разбиваем втулку, полотно и обод диска на ряд сечений, включающих граничные радиусы:

для втулки: х = 0,1312; 0,184; 0,2361;

для полотна: x = 0,2361; 0,294; 0,353; 0,411; 0,469;

где x – текущий радиус.

2. Определяем радиус полного конуса:

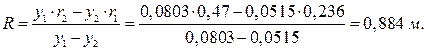
3. Для выбранных сечений определяем:

а) для втулки – отношение x/r_o;

б) для полотна диска – x/R.

По графикам [2, рис. 34, с. 56] и [2, рис. 39, с. 65] определяем:

-для втулки: К₁, К₂, К₃, К′₁, К′₂, К′₃;

-для полотна p_с, p₁, p₂, q_c, q₁, q₂;

Результаты приведены в таблице 3.

4. Определяем напряжения в тонких вращающихся кольцах радиусов r_o,R:

;

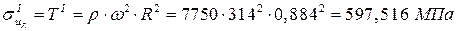Определим методом двух расчётов напряжения в диске.

I расчёт.

Исходные данные:

об/мин;

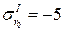МПа (действительное);

МПа – принимаем произвольно.

Результаты первого расчёта приведены в таблице 4.

Расчётные зависимости для втулки:

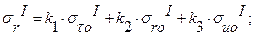
Расчётные зависимости для полотна диска:

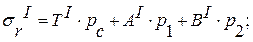
Найдём постоянные интегрирования А^I и В^I. Запишем уравнения для расчёта напряжений на радиусе r₁ конического диска.

;

Значения и находим по уравнениям перехода от ступицы к полотну:

47,453 = 104,565+А^I·2,01+В^I·(-8,01);

65,330 =100,98+А^I·1,595+В^I·13,01;

Получаем значения постоянных интегрирования:

А^I=-26,424; В^I=0,499.

II расчёт

Исходные данные:

об/мин;

МПа;

МПа – принимаем произвольно.

т.к. n^II=0, то и , и .

Результаты второго расчёта приведены в таблице 5.

Расчётные зависимости для втулки:

; .

Расчётные зависимости для полотна диска:

;

.

По формулам перехода определим напряжения на радиусе r₁:

;

Определим А^II и В^II:

44,654 = А^II·2,01+В^II·(-8,01);

40,646= А^II·1,595+ В^II·13,01.

Получаем: А^II = 23,288; В^II =0,269;

Определим коэффициент пересчёта:

Результаты приведены в таблице 6.

Оценка надёжности диска из стали 34ХН1МА:

По III теории прочности:

;

МПа – предел текучести при рабочей температуре;

k_t=2 – для насадных дисков.

Тогда,

.

Следовательно, надежность диска обеспечена.

По данным таблицы 6 строим графики напряжений в диске (рисунок 9).

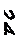Втулка Полотно

x, м 0,1312 0,184 0,2361 x, м 0,2361 0,294 0,353 0,411 0,469

x/r₀ 1,400 1,800 x/R 0,267 0,333 0,399 0,464 0,530

k₁ 0,22 0,35 p_c 0,175 0,171 0,166 0,15 0,138

k₂ 0,78 0,65 p₁ 2,01 2,21 2,495 2,7 3,1

k₃ -0,5 -1 p₂ -8,01 -5,2 -3,52 -2,48 -2

k₁' 0,75 0,65 q_c 0,169 0,168 0,17 0,161 0,152

k₂' 0,78 0,35 q₁ 1,595 1,6 1,79 1,81 2,05

k₃' -0,2 -0,5 q₂ 13,01 7,45 5,05 4,1

Таблица 3

Для контроля: К₁ + К₂ = 1; К′₁ + К′₂ = 1; К′₁ = К₂; К₁ = К′₂.

Втулка Полотно

X,м 0,1312 0,18365 0,2361 x, м 0,2361 0,294 0,353 0,411 0,469

104,57 102,18 99,19 89,63 82,46

-5 -3,75 -3,25 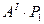-53,11 -58,40 -65,93 -71,34 -81,91

-6,577 -13,153 -4,00 -2,60 -1,76 -1,24 -1,00

-5 11,673 18,597 47,45 41,18 31,50 17,04 -0,46

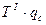
100,98 100,38 101,58 96,20 90,82

-1,1 -1,75 -42,15 -42,28 -47,30 -47,83 -54,17

-2,631 -6,577 6,50 4,99 3,72 2,52 2,05

71,269 56,673 65,33 63,10 58,00 50,89 38,70

Таблица 4

Таблица 5

Втулка Полотно

x, м 0,1312 0,18365 0,2361 x, м 0,236 0,294 0,353 0,411 0,469

k₁·σ_t0^II 17,5 T^II·p_c

k₂·σ_r0^II A^II·p₁ 46,810 51,468 58,105 62,879 72,194

k₃·σ_u0^II B^II·p₂ -2,156 -1,399 -0,947 -0,667 -0,538

σ_r^II 17,5 σ_r^II 44,654 50,068 57,158 62,212 71,656

k'₁·σ_t0^II 37,5 32,5 T^II·q_c

k'₂·σ_r0^II A^II·q₁ 37,145 37,262 41,686 42,152 47,742

k'₃·σ_u0^II B^II·q₂ 3,501 2,691 2,005 1,359 1,103

σ_t^II 37,5 32,5 σ_t^II 40,646 39,953 43,691 43,511 48,845

Таблица 6

Втулка диска Полотно диска

Х, м 0,1312 0,18365 0,2361 x, м 0,2361 0,294 0,353 0,411 0,469

-5 11,673 18,597 47,453 41,182 31,502 17,044 -0,456

6,174 9,823 25,064 28,103 32,082 34,919 40,220

-5 17,848 28,420 72,518 69,285 63,584 51,963 39,765

71,269 56,673 65,330 63,098 57,999 50,894 38,701

28,065 21,049 18,242 22,815 22,425 24,524 24,423 27,416

128,065 92,318 74,916 88,145 85,523 82,523 75,317 66,117

Рисунок 8

3. Расчёт диафрагмы второй ступени давления

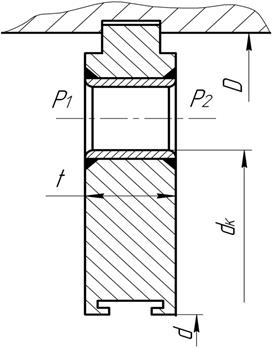Перед диафрагмой давление Р₁ = 1,445 МПа, за ней Р₂ = 1,216 МПа.

Внешний (опорный диаметр) D = 0,879 м,

d = 0,37 м, d_к = 0,8081 м;

толщина диафрагмы t = 0,05 м;

число сопловых лопаток z_д = 40 шт.

Момент сопротивления лопатки относительно оси изгиба W_л = 5,75 см³.

Материал лопаток сталь 20Х13;

σ_д.п = 220 МПа.

Материал диафрагмы - сталь 15Х1МФ;

σ_д.п. = 160 МПа, Е = 180·10³ МПа.

Перепад давлений на диафрагме:

∆Р = Р₁ – Р₂ = 1,573-1,307=0,229 МПа.

Относительный диаметр диафрагменного уплотнения: d/D = 0,421.

Относительная толщина диафрагмы:

Рис. 9.Сварная диафрагма. t/D = 0,0569.

Из рис.56 [1] определяем К_σ = 488.

Максимальное напряжение изгиба, действующее в плоскости симметрии полотна полукольца диафрагмы:

Из рис. 56 [1] определяем К_∆ = 790.

Прогиб диафрагмы в области уплотнения вала:

Прогиб получился <1/3 от расстояния между диафрагмой и диском ступени равный 3,4 мм.

Угловой размер сектора, соответствующего одной сопловой лопатке:

Отношение .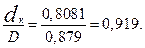

Из рис.57 [1] определяем:

Отсюда изгибающий момент, действующий на лопатку:

Напряжение изгиба в лопатке:

Коэффициент запаса по длительной прочности диафрагмы:

>1,7.

Коэффициент запаса по длительной прочности лопатки:

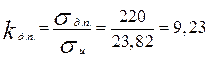>2,3.

Диафрагма по критериям прочности проходит.

4. Определение критической частоты вращения ротора

графоаналитическим методом.

1. Вал вычерчивается в определенном масштабе по длине. K_l=10.

2. После того как вал вычерчен, он разбивается на участки так, чтобы жесткость каждого была постоянна, а участки не особенно длинные.

3. Определим силу тяжести участков: G_i=9,81·m_i.

Таблица №7

№ п/п Масса m_i, кг Сила тяжести G_i, Н

19,135 187,719

12,487 122,493

49,398 484,598

57,922 568,215

189,384 1857,859

408,755 4009,885

194,176 1904,864

137,274 1346,654

140,482 1378,128

133,644 1311,043

138,743 1361,073

177,501 1741,283

181,217 1777,738

211,479 2074,606

190,843 1872,175

221,371 2171,649

235,684 2312,060

243,088 2384,693

351,607 3449,263

364,807 3578,761

455,445 4467,918

524,409 5144,451

562,148 5514,674

622,769 6109,363

63,523 623,158

68,018 667,260

15,090 148,038

20,430 200,420

4. Выбираем масштаб сил: K_G = 200 Н/мм.

5. Строим многоугольник сил. Выбираем полюсное расстояние: Н₁ = 350 мм.

6. Строим веревочный многоугольник под схемой вала. Этот многоугольник будет изображать эпюру изгибающих моментов в определенном масштабе: К_м = K_l· K_G ·H₁; K_м = 10·200·350·10³ =700кН.

Изгибающий момент в любом сечении: М_и_i = K_м · z_i,

где z_i – ордината эпюры в мм.

7. С целью учета переменного диаметра вала принимаем участок с наибольшим диаметром (d_o) за основной и увеличиваем ординаты остальных участков эпюры в отношении моментов инерции сечения вала, для этого вводится коэффициент ;

В нашем случае для сплошного вала: ;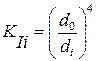

Для учета переменной температуры вала влияющей на величину модуля упругости вводят коэффициент ;

В нашем случае влиянием температурой пренебрегаем, таким образом, первоначально полученная эпюра M_u_зг изменится пропорционально произведению K_Ii·K_E.

8. Для построения упругой линии вала будем считать вал, находящийся под фиктивной нагрузкой измеряемой площадью эпюры изгибающих моментов.

Разделим эту площадь на ряд простых геометрических фигур.

В центре тяжести каждого участка эпюры прикладываем фиктивную силу:

, где f_i – площадь соответствующего участка в масштабе чертежа.

Таблица №8

№ п/п Диамер вала d, м K_I=(d₀/d_i)⁴ Площадь участка в масштабе чертежа f, мм² Значение фиктивной силы R_i, Н·мм²

0,175 8,987 26,931 1,69E+09

0,185 7,196 32,634 1,64E+09

0,205 4,773 108,840 3,64E+09

0,22 3,598 194,507 4,90E+09

0,24 2,541 443,231 7,88E+09

0,26 1,844 418,290 5,40E+09

0,274 1,495 510,793 5,35E+09

0,279 1,391 292,995 2,85E+09

0,279 1,391 336,733 3,28E+09

0,283 1,314 314,088 2,89E+09

0,283 1,314 377,398 3,47E+09

0,287 1,242 405,419 3,53E+09

0,289 1,208 376,558 3,18E+09

0,289 1,208 515,815 4,36E+09

0,295 1,113 377,264 2,94E+09

0,3 1,041 515,094 3,75E+09

0,303 1,000 451,480 3,16E+09

0,296 1,098 428,623 3,29E+09

0,289 1,208 626,802 5,30E+09

0,285 1,278 500,286 4,47E+09

0,279 1,391 620,096 6,04E+09

0,272 1,540 614,388 6,62E+09

0,269 1,610 639,868 7,21E+09

0,263 1,762 600,293 7,40E+09

0,239 2,583 227,828 4,12E+09

0,212 4,173 225,924 6,60E+09

0,192 6,202 63,268 2,75E+09

0,182 7,682 37,374 2,01E+09

9. Строим многоугольник сил в масштабе K_R=6·10⁸ Н·м²/мм.

Определяем полюсное расстояние: Н₂=Е₀·I₀/K_R;

Е₀=2,1·10¹¹ Н/м², ;

Так как величина Н₂ получилась большой, то уменьшаем её в k раз. Таким образом H₂’=Н₂/k.

Примем k = 804,518, тогда:

Строим многоугольник фиктивных сил и упругую линию прогибов. Определяем истинные прогибы вала, умножив снятые с чертежа величины на K_l/k = 10/804,518= 0,01101, т.е. в одном миллиметре чертежа будет 0,0110 1мм прогиба.

Таблица №9

№ п/п Стрела прогиба под грузом, по чертежу y, мм Истинное значение стрелы прогиба, y, мм G·y, Н·м m·y², кг·м²

2,98 0,0328 0,0062 2,056E-08

7,31 0,0804 0,0098 8,074E-08

11,53 0,1268 0,0615 7,946E-07

17,3 0,1903 0,1081 2,098E-06

24,44 0,2688 0,4995 1,369E-05

30,65 0,3372 1,3519 4,646E-05

35,16 0,3868 0,7367 2,905E-05

38,1 0,4191 0,5644 2,411E-05

39,97 0,4397 0,6059 2,716E-05

41,56 0,4572 0,5994 2,793E-05

42,96 0,4726 0,6432 3,098E-05

44,2 0,4862 0,8466 4,196E-05

45,12 0,4963 0,8823 4,464E-05

45,85 0,5044 1,0463 5,379E-05

46,19 0,5081 0,9512 4,927E-05

46,28 0,5091 1,1055 5,737E-05

46,04 0,5064 1,1709 6,045E-05

45,56 0,5012 1,1951 6,105E-05

44,66 0,4913 1,6945 8,486E-05

43,11 0,4742 1,6971 8,204E-05

41,02 0,4512 2,0160 9,273E-05

37,81 0,4159 2,1396 9,071E-05

33,26 0,3659 2,0176 7,525E-05

26,7 0,2937 1,7943 5,372E-05

20,11 0,2212 0,1378 3,108E-06

14,51 0,1596 0,1065 1,733E-06

8,49 0,0934 0,0138 1,316E-07

3,2 0,0352 0,0071 2,531E-08

10.

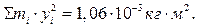
11. Определяем критическую частоту вращения ротора:

12. Оценим виброустойчивость вала:

1,4·n_кр1 < n_раб < 0,7·n_кр2;

n_раб = 3000 об/мин; n_кр1 = 1440,531 об/мин; n_кр2 = 3,25·n_кр1 = 3,25·1440,531 = 4681,725 об/мин;

2016,7434 < 3000 <3277,208;

Вывод: конструкция вала не удовлетворяет условиям прочности.

5. Гидродинамический расчёт опорного и упорного подшипников

5.1 Расчёт опорного подшипника

Исходные данные:

диаметр шейки вала d₁ = 0,175 м; d₂ = 0,182 м;

длина шейки вала l₁ = 0,16 м; l₂ = 0,14 м;

частота вращения ротора n = 3000 об/мин;

грузоподъёмность подшипника Р = 31714,895 Н.

Примем величину диаметрального зазора δ₁ = 0,45 мм, δ₂= 0,5 мм [2]; следовательно: ψ₁ = δ₁/d₁ = 0,45/0,175 = 0,0026;

ψ₂ = δ₂/d₂ = 0,5/0,182 = 0,00275.

Окружная скорость шейки:

u₁ = πd₁n/60 = π·0,175·3000/60 = 27,489 м/с.

u₂ = πd₂n/60 = π·0,182·3000/60 = 28,588 м/с.

Отношение l₁/d₁ = 0,914; l₂/d₂ = 0,769.

Плотность масла ρ = 900 кг/м³ заданная средней температурой масла в подшипнике t_ср = 50 °С.

Коэффициент динамической вязкости при t_ср = 50 °С; μ =0,0183 Н·с/м².

Определим коэффициент грузоподъёмности:

По рис. 314 [3] определяем

Подсчитаем минимальную толщину масляной плёнки:

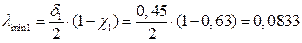мм;

мм.

Жидкостное трение в подшипнике осуществляется при коэффициенте запаса надёжности:

; λ_кр = 0,01…0,015;

К₁ = 0,0833/0,015 = 5,55; К₂ = 0,07/0,015 = 4,66.

По рис. 315 [3] определим величины: f₁/ψ₁ = 1,9; f₂/ψ₂ = 1,8

Коэффициент трения в нижней половине подшипника:

f₁ = 1,9·0,0026 = 0,00489; f₂ = 1,8·0,00275= 0,00495.

Коэффициент трения в верхней половине подшипника:

f′₁ = 1,5∙μ∙u₁∙l₁/ψ₁∙Р = 1,5∙ 0,0183·27,489·0,16/(0,0026·31714,895) = 0,00148;

f′₂ = 1,5∙μ∙u₂∙l₂/ψ₂∙Р = 1,5·0,0183·28,588·0,14/(0,00275·31714,895) = 0,00126.

Мощность, затрачиваемая на трение:

N₁ = P· (f₁ + f′₁)·u₁/10³ = 31714,89·(0,00489+ 0,00148)· 27,5/ 1000 = 5,55 кВт;

N₂ = P· (f₂ + f′₂)·u₂/10³ = 31714,89·(0,00495+ 0,0013)· 28,588/1000 = 5,627 кВт;

Коэффициент расхода масла через нижний вкладыш (рис. 316) [2]:

Q₁₁/ψ₁u₁d₁l₁ = 0,14; Q₁₂/ψ₂u₂d₂l₂ = 0,18.

Расход масла вытекающего через торцы подшипника под действием давления масляного клина:

Q₁₁ = 0,14·0,0026·27,5·0,175·0,16 = 0,000277 м³/с;

Q₁₂ = 0,18·0,00275·28,588·0,182·0,14 = 0,00036 м³/с.

Под действием избыточного давления Р_е=5·10⁴ Н/м² масло подводится к подшипнику и вытекает через торцы подшипника.

Расход масла:

где Р_{ср 1} = Р/l₁·d₁ = 31714,895/0,16·0,175 = 1132675 H;

P_cp₂ = P/l₂·d₂ = 22844,97/0,14·0,182 = 1244698 H;

Полный расход масла:

Q₁ = Q₁₁ + Q₂₁ = 0,000277 + 0,0002094 = 0,0004864 м³/с;

Q₂ = Q₁₂ + Q₂₂ = 0,00036 + 0,000336= 0,000697 м³/с.

Повышение температуры масла в подшипнике:

= 6,435 °С;

= 4,556 °С,

где с_p = 1,97 кДж/кг·град – удельная теплоёмкость масла.

Температура масла при входе в подшипник:

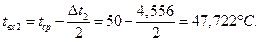
Температура масла на выходе из подшипника:

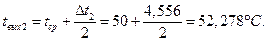
Обе величины являются приемлемыми, т.к. температура на входе в подшипник не должна быть ниже 35°С, а на выходе не выше 70°С.

5.2 Расчёт упорного подшипника

Исходные данные:

центральный угол охвата θ = 40°, наружный радиус сегментов R = 0,165 м, внутренний радиус колодки r = 0,0875 м, ширина колодки b = 0,0775 м, b/r = 0,886, число сегментов Z = 8, осевая нагрузка на подшипник Р = 43385,4 Н, n = 3000 об/мин, θ = 0,698 рад.

По величинам θ и b/r определяем коэффициенты по рис. 55[1]:

К₁ =2,351; К₂ = 0,063; К₃ = 0,357; К₄ = 0,77; К₅ = 0,0087;

Рабочая поверхность одной колодки:

F₁ = К₆ r² = 0,8922·0,0875² = 0,00683 м²;

Усилие, приходящееся на одну колодку:

P₁ = P/Z = 43385,4/8 = 5423,175 Н;

Среднее удельное давление:

P_ср = P₁

⇐ Предыдущая 12

Воспользуйтесь поиском по сайту: