 |
Метод использования канонической формы Ленбергера
|
|
|
|
Синтезировать наблюдатель Люенбергера полного порядка с распределением корней характеристического полинома по биномиальной стандартной линейной форме и среднегеометрическим корнем, равным
.
Примем 
В качестве измеряемой координаты вектора состояния принять х1.
Динамическая подсистема для оценивания вектора координат состояния строится на основе математической модели ОУ путем ее дополнения «стабилизирующей добавкой»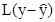 
[1]. Так как в системе производится прямое измерение х2, матрица выхода 
,
а сам вектор выходных (измеряемых) переменных: 
.
На основании последних соотношений и системы уравнений
Математическая модель наблюдателя Люенбергера полного порядка:
Проверка условия наблюдаемости объекта
выражаемого требованием равенства ранга матрицы наблюдаемости порядку ОУ rang(Н) = 2 [1].
Матрица наблюдаемости для принятого объекта (3.1) равна
,
= 
rang(Н) = 2, что удовлетворяет условию наблюдаемости.
Включение в подсистему оценивания координат «стабилизирующей добавки» влияет на собственные динамические свойства наблюдателя, которые должны обеспечить требуемую форму и качество свободных составляющих переходного процесса. По этой причине элементы матрицы L определяются из нормированного характеристического полинома Dн(р), который предлагается принять соответствующим биномиальной стандартной линейной форме [1]:
Увеличение среднегеометрического корня 
по соотношению к 
позволяет разнести темпы процессов в синтезированной САУ с модальным регулятором и в подсистеме оценивания координат состояния, в результате чего наличие наблюдателя Люенбергера практически не оказывает влияния на динамику системы управления [1].
|
|
|
Характеристический полином наблюдателя
Приравняв соответствующие коэффициенты 
и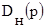 
, получим:
Структурная схема синтезированной замкнутой системы с наблюдателем Люенбергера полного порядка и модальным регулятором:
Рис. 1. Структурная схема СМУ с наблюдателем полного порядка.
Рис.2. Переходные процессы «ОУ + НПП»
а) по управляющему воздействию с нулевыми начальными условиями,
б) по возмущающему воздействию с нулевыми начальными условиями,
в) по управляющему воздействию с отклонениями по начальным условиям
Работа наблюдателя Люенбергера при отклонениях по начальным условиям: в момент времени от 0 до 1с координаты наблюдателя и ОУ не совпадают, далее оценки втягиваются и наблюдатель отслеживает работу координат ОУ для координаты х2
Стандартные реакции системы управления
В ряде случаев система управления не позволяет обеспечить приемлемую точность слежения за задающим воздействием. Для решения поставленной задачи возможны два способа. Первый способ состоит в введении в алгоритм управления дополнительной интегрирующей связи в канал ошибки слежения, которая повышает порядок астатизма. Тем самым повышается точность работы САУ. Такой способ управления называется изодромное управление. Второй способ состоит во введении дополнительных прямых связей по внешнему воздействию, которые компенсируют влияние этого воздействия и позволяют функционировать САУ с требуемой установившейся ошибкой. Такой способ управления имеет название метод комбинированного управления или метод динамической компенсации.
ЗАКЛЮЧЕНИЕ
В ходе выполнения данной работы была рассмотрены все вопросы, рассматриваемые в курсе «Информатика».
Можно заметить, что с помощью метода модального управления можно получить желаемый вид переходного процесса с необходимым перерегулированием и временем переходного процесса, используя стандартные распределения нормированных коэффициентов, что свидетельствует о высокой точности расчетов по данному методу.
|
|
|
Список использованной литературы
1. Бургин Б.Ш. Анализ и синтез двухмассовых электромеханических систем: Монография / Новосиб. электротехн. ин-т. – Новосибирск, 1992. 199 с.
2. Яворский В. Н., Макшанов В. И., Ермолин В. П. Проектирование нелинейных следящих систем с тиристорным управлением исполнительным двигателем. – Л.: Энергия, 1978. 208 с.
2. Кириллов В.И. Многоканальные системы управления. Минск. Новое издание, 2003г.
3. Скляр Б. Цифровая связь. Теоретические основы и практическое применение. Москва. Вильямс, 2003г.
|
|
|
