Составление и анализ математического описания

Составление, решение и анализ математического описания химических процессов в системе Г – Ж существенно затрудняются сложностью и недостаточной изученностью массопереноса в каждой из фаз и гидродинамических условий вблизи границы раздела фаз. Наиболее наглядная модель этих явлений была разработана в самой ранней – пленочной – теории массопереноса. Многие положения пленочной теории принимаются и в настоящее время, хотя уже показано, что эта теория исходит из слишком упрощенных представлений и имеет много недостатков. Были предложены другие более приближенные к реальности модели массопереноса-проницания, обновления поверхности, диффузионного пограничного слоя и т.д. Однако ни одна из них не является достаточно полной, и возможно поэтому расчетные результаты, полученные на основе различных моделей, практически совпадают. Учитывая это, мы при дальнейшем рассмотрении будем пользоваться пленочной моделью как наиболее простой и наглядной. Напомним основные положения пленочной теории (рис. 2.4).

Рис. 2.4. Пленочная модель массопереноса в системе Г – Ж:

Г – граница ядра потока газа и газовой пленки; Ж – граница ядра потока жидкости и жидкостной пленки; ГРФ – граница раздела фаз.

 

1. В обеих фазах непосредственно у межфазной границы имеется тонкий слой, представляющий собой неподвижную или ламинарно текущую пленку. Внутри пленок перенос вещества осуществляется только вследствие стационарной молекулярной диффузии, описываемой уравнением

, (2.38)

где D – коэффициент диффузии; х – направление диффузии. Проинтегрировав уравнение (2.38), получим коэффициент массопереноса

, (2.39)

где δ – толщина пленки.

2. На границе раздела фаз существует равновесие, для которого применим закон Генри

, (2.40)

где Н – константа фазового равновесия.

3. В ядре фаз перенос вещества осуществляется за счет быстрого конвективного, движения и турбулентного перемешивания; поэтому в ядре фазы вещества равномерно распределены и их концентрации постоянны по объему. В результате этого градиенты концентраций возникают лишь внутри пленок, в которых сосредоточено все диффузионное сопротивление массопереносу. Поскольку при равновесии сопротивление на границе раздела фаз отсутствует, то общее сопротивление массопередаче состоит из сопротивления каждой из фаз, т.е. существует аддитивность фазовых сопротивлений. В соответствии с этим коэффициент массопередачи из газовой в жидкую фазу можно выразить соотношением

. (2.41)

Согласно пленочной теории, скорость переноса газообразного вещества из ядра газового потока к поверхности контакта фаз определяется уравнением

, (2.42)

а скорость переноса растворенного вещества от межфазной границы к ядру жидкостного потока уравнением

. (2.43)

где Р ⁰ – парциальное давление вещества в ядре газового потока; С⁰ – концентрация растворенного вещества в ядре жидкостного потока.

Скорость переноса вещества в пределах жидкостной пленки от межфазной границы к течению на расстоянии δ₁ определяется выражением

, (2.44)

а скорость переноса из ядра жидкостного потока к этому же сечению выражением

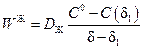. (2.45)

При рассмотрении химических процессов в системе обычно выделяют три режима, в которых составление, решение и анализ математического описания значительно упрощаются: 1) режим мгновенной реакции; 2) режим быстрой реакции; 3) режим медленной реакции.

Режим мгновенной реакции. Рассмотрим процесс (рис. 2.5, а), сопровождающийся протеканием в жидкой фазе мгновенной необратимой реакции

.

В этом случае реагенты диффундируют навстречу друг другу и мгновенно реагируют внутри жидкостной пленки на реакционной поверхности, расположенной на расстоянии δ₁ от поверхности контакта фаз. В результате мгновенного и необратимого взаимодействия концентрации реагентов в зоне реакции падают до нуля.

Рис. 2.5 Режим мгновенной реакции в системе Г – Ж:

а) , ;

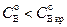б) , ;

в) , ;

г) .

Составим математическое описание стационарного протекания химического процесса с мгновенной реакцией исходя из условия стационарности:

(2.46)

В соответствии со схемой процесса (см. рис. 2.5, а) и уравнениями массопереноса (2.42), (2.44) и (2.45) уравнения скорости отдельных стадий имеют вид

С учетом условий стационарности (2.46), равновесия (2.40) и значений концентраций в зоне реакции С _А(δ₁) = С _В(δ₁) = 0 получим следующее математическое описание процесса:

 

(2.47)–(2.49)

Решив систему уравнений (2.47)–(2.49), можно найти δ₁, и W _набл. Совместным решением (2.48) и (2.49)

(2.50)

найдем

. (2.51)

Тогда

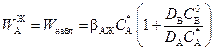. (2.52)

Совместно решив уравнения (2.52) и (2.47)

,

найдем

. (2.53)

Подставив (2.53) в (2.47), после преобразований получим

, (2.54)

где К _АГ – коэффициент массопередачи реагента А из газа в жидкость, определяемый по уравнению (2.41).

Анализ полученного математического описания показывает, что химический процесс с мгновенной реакцией протекает в диффузионной области, поскольку его скорость, определяемая по уравнению (2.54), зависит только от скорости диффузии реагентов к зоне реакции и не зависит от кинетики реакции; диффузионное сопротивление оказывают обе пограничные пленки.

Зона реакции, согласно (2.51), может перемещаться при изменении соотношений и 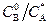. При увеличении этих соотношений зона реакции смещается в сторону границы раздела фаз, при уменьшении – к внутренней поверхности пленки жидкой фазы. При этом могут иметь место два предельных случая.

1. Зона реакции находится на границе фаз: δ₁ = 0 (см. рис. 2.5, б). Из (2.51) следует, что при этом . Согласно (2.53), такой случай возможен при условии, что числитель равен нулю. Отсюда критическое значение соответствующее этому случаю,

.

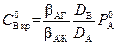При наблюдаемая скорость процесса, согласно (2.47),

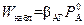. (2.55)

Это отвечает нулевому сопротивлению жидкой фазы; все диффузионное сопротивление сосредоточено в газовой пленке. Это же справедливо и при , но в этом случае концентрация реагента В у границы раздела фаз равна не нулю, а некоторой величине 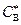(см. рис. 2.5, в). Диффузионное сопротивление остается тем же, и применение для ускорения процесса бесполезно.

2. Зона реакции находится на внутренней поверхности пленки жидкой фазы: δ₁ = δ (см. рис. 2.5, г). Из (2.50) следует, что при этом , и тогда, согласно (2.53) и (2.54), получим

;

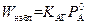. (2.56)

Режим мгновенной реакции имеет место при протекании ионных реакций, заключающихся только в обмене протонов (абсорбция кислоты сильным основанием или основания – сильной кислотой); ему соответствуют также реакции второго порядка с константой скорости более 10⁵ м³/(кмоль · с). Наибольшее практическое значение приобрели процессы поглощения аммиака серной, фосфорной и другими кислотами; оксида серы (IV) и сероводорода – щелочами; реакции высших спиртов с SО₃ при получении ПАВ, сульфирование олеумом реакционноспособных ароматических углеводородов, алкилирование бензола пропиленом в присутствии каталитического комплекса хлорида алюминия и др.

Режим быстрой реакции. По мере уменьшения скорости химической реакции (по сравнению с мгновенно протекающим взаимодействием) зона реакции расширяется. При этом возможны две схемы протекания процесса.

1. Зона реакции ограничивается пределами пограничной пленки жидкой фазы (рис. 2.6, а). Это значит, что за время диффузии через жидкостную пленку растворенный реагент А полностью превращается в продукт реакции и, следовательно, не поступает в ядро жидкостного потока .

Рис. 2.6. Режим быстрой реакции в системе Г—Ж:

а) ; б) .

2. Зона реакции занимает всю площадь пограничной пленки жидкости и часть объема ядра жидкостного потока (см. рис. 2.6, б). Это значит, что за время диффузии через пленку растворенный реагент А превращается неполностью и некоторая доля его переходит в ядро потока, где химическая реакция продолжается.

При математическом описании процесса, протекающего в жидкостной пленке, учитывается совместное действие диффузии и реакции. В стационарных условиях, согласно (2.38),

.

Наиболее простое аналитическое решение математического описания режима быстрой реакции имеется для псевдопервого порядка, когда при больших концентрациях реагента В () скорость реакции r = kC _A. Оно применимо для многих каталитических реакций (например, поглощение СО₂ растворами Na₂CО₃ или К₂СО₃ в присутствии катализаторов – арсенита или гипохлорита Na). Однако и это решение является сложным и громоздким. Анализ решения прежде всего показывает: 1) процесс протекает в смешанной диффузионно-кинетической области; 2) характер изменения концентрации растворенного реагента А в жидкостной пленке С _А = f (х) вследствие химического превращения является нелинейным. Зависимости С _А = f (х) для схемы, изображенной на рис 2.6, а, при разных значениях комплекса 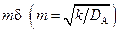представлены на рис. 2.7. Из него видно, что чем быстрее идет химическая реакция по сравнению с диффузией, т.е. чем больше , тем круче изгиб кривых и тем больше градиент концентрации на начальных участках. Линейная зависимость С _А = f (х) соответствует 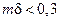и, следовательно, имеет место при протекании относительно медленных химических реакций.

Рис. 2.7. Профиль изменения концентрации растворенного газообразного реагента в жидкостной пленке в зависимости от величины соотношения константы скорости реакции и коэффициента диффузии.

 

Режим медленной реакции характеризуется столь малой скоростью реакции, что за время диффузии растворенного реагента А через жидкостную пленку его химическим превращением можно пренебречь. Реакция протекает в основной массе жидкости, зависимость С _А = f (х) в пределах жидкостной пленки имеет линейный характер (рис. 2.8).

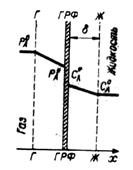
Рис. 2.8. Режим медленной реакции в системе Г—Ж.

 

Составим математическое описание химического процесса в режиме медленной реакции псевдопервого порядка, скорость которой

(2.57)

В стационарных условиях

(2.58)

Уравнения скорости отдельных стадий в соответствии с (2.42), (2.43) и (2.57), имеют вид

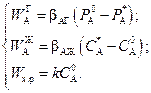
Прежде чем перейти к условию стационарности (2.58), обратим внимание, что

; ; ,

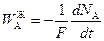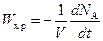где F – поверхность контакта фаз; V – объем жидкой фазы. Это требует введения выражения

(2.59)

где поверхностная константа скорости реакции k _f = kV / F. С учетом (2.59) условие стационарности (2.58) примет вид

(2.60)–(2.62)

Система уравнений (2.60)–(2.62) позволяет найти , и . Совместным решением (2.60) и (2.61)

найдем

. (2.63)

Подставив (2.63) в (2.60), получим уравнение скорости переноса реагента А из газовой фазы к ядру жидкостного потока, т.е. к зоне реакции

. (2.64)

Совместно решив (2.64) и (2.62), найдем

. (2.65)

Подставив (2.65) в (2.62), получим уравнение наблюдаемой скорости химического превращения

. (2.66)

Уравнение (2.66) показывает, что процесс, протекающий по схеме, представленной па рис. 2.8, идет в смешанной диффузионно-кинетической области. Роль наблюдаемой константы скорости играет выражение

,

соответствующее правилу аддитивности, по которому в рассматриваемом режиме общее сопротивление состоит из химического и диффузионного сопротивлений. Относительная роль этих сопротивлений изменяется в зависимости от соотношения величин k _f и Н _А К _АГ. При 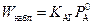, и медленная реакция протекает в диффузионной области.

При с учетом

; , (11.67)

и процесс протекает в кинетической области; его скорость определяется только скоростью реакции в жидкой фазе.

В кинетической области протекают такие сравнительно медленные химические реакции, как сульфирование, нитрование ароматических соединений, гидрирование, значительная часть процессов жидкофазного хлорирования и окисления.

Область применения схем, представленных на рис. 2.6 и 2.8, может быть определена по графику (рис. 2.9). С ростом mδ все меньшая доля реагента А проходит через пограничный слой в объем жидкости, т.е. все большая часть реагента А превращается в пленке. При mδ > 5 φ → 0 процесс протекает по схеме, приведенной на рис. 2.6, а; при mδ > 0,3 φ → 1 процесс протекает по схеме, приведенной на рис. 2.8; при 0,3 < mδ < 5 справедлива схема, приведенная на рис. 2.6, б.

Рис. 2.9. Зависимость доли φ растворенного газообразного реагента А, непрореагировавшего в пленке и перешедшего в ядро потока жидкости, от соотношения констант скорости реакции и коэффициента диффузии .

Важнейшей характеристикой химических процессов в системе Г—Ж является фактор ускорения

,

показывающий, во сколько раз увеличивается количество поглощенного газа при химическом процессе по сравнению с физической абсорбцией . Фактор ускорения может принимать значения от Ф = 1 для медленных реакций до Ф → ∞ для мгновенных реакций на поверхности контакта фаз.

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: