Тема: «Пространственная система сил»

Тема: «Пара сил. Момент пары сил»

Пример 1. Дана пара сил | F₁ | = | F'₁ | = 42кН; плечо 2 м. Заменить заданную пару сил эквивалентной парой с плечом 0,7 м (рис. 4.5).

Решение

Пары сил эквивалентны, ес­ли моменты этих пар численно равны:

 

Пример 2. Дана система пар сил (рис. 4.6). Определить момент результирующей пары.

Решение

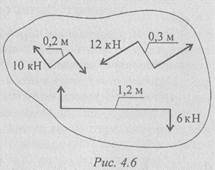
Момент результирующей па­ры равен алгебраической сумме моментов пар системы:

Подставив численные значе­ния, получим:

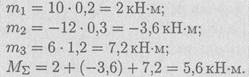
Знак свидетельствует о том, что момент вызывает вращение по часовой стрелке. Величину силы и плеча определить не удается.

Примечание. Чтобы уравновесить данную систему пар, необходимо приложить пару сил, равную по модулю и направленную в обратную сторону. Такую пару сил называют уравновешивающей.

Пример 3. Рассчитать сумму моментов сил относительно точки 0 (рис. 4.7).

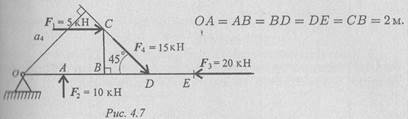
Решение

1. Момент силы относительно точки численно равен произведению модуля силы на плечо силы.

2. Момент силы равен нулю, если линия действия силы проходит через точку.

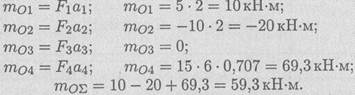
Тема: «Плоская система произвольно расположенных сил»

Пример 1. Найти момент присоединенной пары при переносе силыF₃ в точку В (рис. 5.3). F = 10кН; F₂ = 15кН; F₃ = 18кН; а = 0,2 м.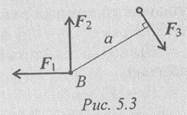

Решение

Используем теорему Пуансо.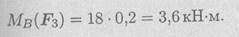

 

Пример 2. Найти главный вектор системы (рис. 5.4). F1 = 10кН; F₂= 16 кН; F₃= 12 кН; т = 60кН-м.

Решение

Главный вектор равен геометрической сумме сил:

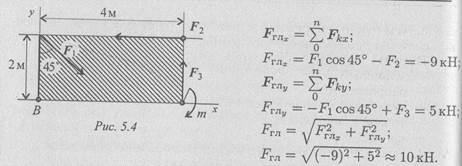
Пример 3. Найти главный момент системы относительно точ­ки В (использовать данные примера 2).

Решение

Главный момент равен алгебраической сумме моментов сил от­носительно точки приведения:

Пример 4. К телу приложена уравновешенная система сил (рис. 5.5). Две из них неизвестны. Определить неизвестные силы. F1 = 10 кН; F 2 = 16 кН.

Наносим оси координат и ис­пользуем уравнения равновесия:

Пример 5. Консольная (защемленная) балка нагружена со­средоточенными силами и парой сил (рис. 6.7). Определить реакции заделки.

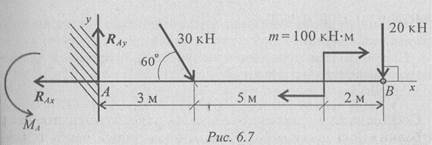
Решение

1. В заделке может возникнуть реакция, представляемая двумя составляющими (R_Ay, R_Ах), иреактивный момент М_А. Наносим на схему балки возможные направления реакций.

Замечание. Если направления выбраны неверно, при расчётах получим отрицательные значения реакций.

В силу малой ширины балки считают, что все точки балки находятся на одной прямой; все три неизвестные реакции приложены в одной точке. Для решения удобно использовать систему уравнений равновесия в первой форме. Каждое уравнение будет содержать одну неизвестную.

2. Используем систему уравнений:

 

Знаки полученных реакций (+), следовательно, направления ре­акций выбраны верно.

3. Для проверки правильности решения составляем уравнение моментов относительно точки В.

Проверка:

Подставляем значения полученных реакций:

-377,94 + 45,98 • 10 - 210 • 0,866 + 100 = 0;

-559,8 + 559,8 = 0.

Решение выполнено верно.

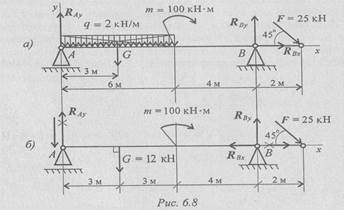
Пример 6. Двухопорная балка с шарнирными опорами А и В нагружена сосредоточенной силой F, распределенной нагрузкой с интенсивностью q и парой сил с моментом m (рис. 6.8а). Определить реакции опор.

Решение

1. Левая опора (точка А) — подвижный шарнир, здесь реакция направлена перпендикулярно опорной поверхности.

Правая опора (точка В) — неподвижный шарнир, здесь наносим две составляющие реакции вдоль осей координат. Ось Ох совмещаем продольной осью балки.

2. Поскольку на схеме возникнут две неизвестные вертикальные реакции, использовать первую форму уравнений равновесия нецелесообразно.

3. Заменяем распределенную нагрузку сосредоточенной:

G = ql, G = 2●6 = 12 кН.

Сосредоточенную силу помещаем в середине пролета(рис. 6.8б).

4. Наносим возможные реакции в опорах (направление произвольное).

5. Для решения выбираем уравнение равновесия в виде

 

6. Составляем уравнения моментов относительно точек крепления:

 

Проверка:

 

-5,1 - 12 + 34,6 - 25 • 0,7 = 0.

Следовательно, реакции определены верно.

Знак «минус» у реакций R_AY и R_BX указывает на то, что они направлены в противоположную сторону.

Тема: «Пространственная система сил»

Пример 1. На тело в форме куба с ребром а — 10 см действуют три силы (рис. 7.6). Определить моменты сил относительно осей координат, совпадающих с ребрами куба.

Решение

1. Моменты сил относительно оси Ох:

 

2. Моменты сил относительно оси Оу:

3. Моменты сил относительно оси Oz:

 

Пример 2. На горизонтальном валу закреплены два колеса,), r₁= 0, 4м;

r₂ = 0,8м. Остальные размеры — на рис. 7.7. К колесу 1 приложена сила F₁, к колесу 2 — силы F₂ = 12 кН, F₃ = 4кН. Определить силу F1 и реакции в шарнирах А и В в состоянии равновесия.

 

Нап омним:

1. При равновесии выполняютсяшесть уравнений равновесия. Уравнения моментов следует составлять относительно опор А и В.

2. Силы F₂ // Ox; F₁ // Oy; F₃ // Oy.

Моменты этих сил относительно соответствующих осей равны нулю.

Расчёт следует завершитьпроверкой, использовав дополнительные уравнения равновесия.

Решение

Определяем силу F1, составив уравнение моментов сил относительно оси

 

Oz:

Определяем реакции в опоре А. На опоре действуют две составляющие реакции ( Y_a; X_a ).

Составляем уравнение моментов сил относительно оси Ох' (в опоре В).

Поворот вокруг оси Ох' не происходит:

 

Знак «минус» означает, что реакция направлена в противоположную сторону.

Поворот вокруг оси Оу' не происходит, составляем уравнение моментов сил относительно оси Оу' (в опоре В):

3. Определяем реакции в опоре В. На опоре действуют две со­ставляющие реакции (Х_в; У_в). Составляем уравнение моментов сил относительно оси Ох (опора А):

Составляем уравнение моментов относительно оси Оу (опора А):

4. Проверка. Используем уравнения проекций:

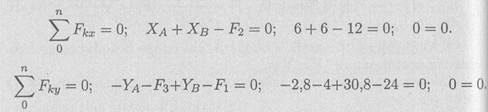
Следовательно, реакции определены верно.

Тема: «Центр тяжести»

Пример 1. Определить положение центра тяжести фигуры, представленной на рис. 8.4.

Решение

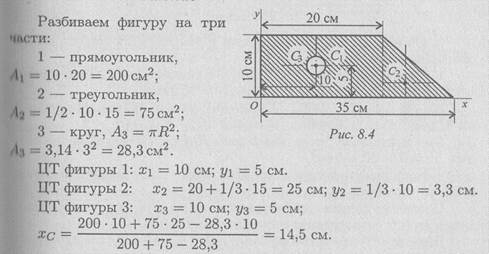
Аналогично определяется Yс

Пример 2. Определить координаты центра тяжести составного сечения. Сечение состоит из листа и прокатных профилей (рис. 8.5).

Примечание. Часто рамы сваривают из разных профилей, получая необходимую конструкцию. Таким образом, уменьшается расход металла и образуется конструкция высокой прочности.

 

Для стандартных прокатных профилей собственные геометрические характеристики известны. Они приводятся в соответствующих таблицах прокатного профиля.

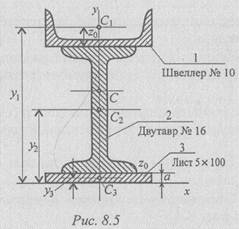
Решение

1. Обозначим фигуры номерами и выпишем из таблиц необхо­димые данные:

1 — швеллер № 10 (ГОСТ 8240-89); высота h = 100 мм; ширина полки b = 46 мм; площадь сечения А₁ = 10,9 см²;

2 — двутавр № 16 (ГОСТ 8239-89); высота 160 мм; ширина пол­ки 81мм; площадь сечения А₂ = 20,2 см²;

 

Поделиться:

Воспользуйтесь поиском по сайту: