Оценка адекватности модели

Оценить качество модели в целом можно, основываясь на минимальности отклонения фактиче­ских значений результативного признака от теоретических, рас­считанных по уравнению регрессии.

Величина отклонений эмпирических и расчетных значе­ний по каждому наблюдению представляет собой ошибку аппроксимации. Их число соответствует объему сово­купности.

Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппрокси­мации, как среднюю арифметическую простую:

Возможно и другое определение средней ошибки аппрок­симации, как

Oднако первая формула используется чаще.

Верификация регрессионных моделей

При подстановке в уравнение регрессии = а + bх соответствующего значения х можно определить предсказывае­мое (прогнозируемое) значение у_p как вариант точечного про­гноза у_k при х_р= х_k. Однако точечный прогноз явно не будет от­вечать реальным событиям. Поэтому его необходимо дополнить расчетом стандартной ошибки m_vx и соответственно интер­вальной оценкой прогнозного значения: y-m_yx ≤ yp ≤ y+m_yx

Для построения формулы, позволяющей определить ве­личину стандартной ошибки m_vx необходимо обратиться к уравнению регрессии: = a + bx

Подставив в это уравнение выражение параметра a (), уравнение регрессии примет вид:

Отсюда следует, что стандартная ошибка m_vx зависит от ошибки и ошибки коэффициента регрессии b: m² =m ²+m_b²(x- )²

Из теории выборочного исследования статистических данных известно: , однако в качестве меры оценки следует использовать остаточную дисперсию на одну степень свободы ². Соответственно получим формулу для расчета среднего значения переменной у:

Ошибка коэффициента регрессии b определяется по формуле: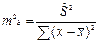

Считая, что предсказываемое значение фактора х_р= х_k, по­лучим формулу расчета стандартной ошибки прогнозируемого значения результативного признака по уравнению регрессии:

Рассмотренная формула стандартной ошибки предсказы­ваемого значения при заданном х_р = х_k характеризует ошибку линии регрессии. Величина стандартной ошибки m_vx достигает максимума при х_р = х_k = , возрастает по мере удаления х_р от в любом направлении, т. е. чем больше разность х_р от , тем больше т_{у x}. Наилучшие результаты прогноза следует ожи­дать, если факторный признак х_р находится в центре области наблюдений х, и нельзя ожидать хороших результатов прогноза при удалении х_р от . Если значение х_р оказывается за пре­делами наблюдаемых значений факторных признаков х, исполь­зуемых при построении модели, то результаты прогноза ухудшаются по мере отклонения х_р от области наблюдаемых значе­ний фактора х.

Графически доверительные границы для у_х представля­ют собой гиперболы, расположенные по обе стороны от линии регрессии.

Фактические значения у варьируют около среднего значе­ния . Индивидуальные значения у отличаются от на вели­чину случайной ошибки, дисперсия которой оценивается как остаточная дисперсия на одну степень свободы S². Поэтому ошибка индивидуального предсказываемого значения у_р долж­на включать не только стандартную ошибку m _vx, но и случай­ную ошибку.

 

Доверительный интервал линии регрессии:

а - верхняя доверительная граница у_p;

b- линия регрессия = a + bx;

с - доверительный интервал для у_р при заданных х_р;

d- нижняя граница для у_р.

Средняя ошибка прогнозируемого индивидуального зна­чения у при х_р= х_k составит:

Тогда с заданной вероятностью доверитель­ный интервал для у_р при заданном х_р = x_k составит:

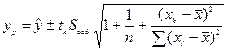, где t_k – критическое (табличное) значение t -критерия Стьюдента для соответствующего уровня значимости α = 1- р и числа степеней свободы (n - 2).

При прогнозировании на основе уравнения регрессии не­обходимо помнить, что величина прогноза зависит не только от величины стандартной ошибки индивидуального значения у_р, но и от точности прогноза значения фактора х.

Рассмотренная формула стандартной ошибки индивиду­ального значения признака m_{yi ( xk )} может использоваться для оценки существенности различия предсказываемого значения, исходя из регрессионной модели и выдвинутой гипотезы разви­тия событий. Для этой цели используется односторонний t-критерий Стьюдента:

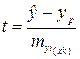
Полученное фактическое значение одностороннего t-критерия Стьюдента сравнивается с табличным, и если t_факт ^> t_табл, то предполагаемое значение значимо (существен­но) отличается от прогнозируемого по модели, и наоборот.

 

Пример

Менеджер новой чебуречной не уверен в правильности выбранной цены на чебуреки, поэтому в течение 12 недель он варьирует цену и записывает количество проданных чебуреков. Полученные данные приведены в таблице:

t	p	q	t	p	q
	12,3			12,8
	11,5			9,9
	11,0			12,2
	12,0			12,5
	13,5			13,0
	12,5			10,5

 

Постройте линейное уравнение регрессии, характеризующее зависимость продаж от изменения цены; оцените параметры модели; на основании полученной модели определите оптимальную цену единицы товара; рассчитайте возможный объем продаж исходя из рекомендуемой цены.

 

x	y	x 2	y 2	x × y
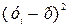
12.3		151.29		9778.5	777.57	1144.69	303.81	0.11	0.0219
11.5		132.25		10522.5	903.76	7424.69	126.41	0.23	0.0123
					982.62	18541.36	310.6	0.95	0.0183
					824.89	3990.03	4503.75	0.000625	0.0752
13.5		182.25		7897.5	588.29	59454.69	10.82	2.33	0.005622
12.5		156.25			746.02	34163.36	10408.69	0.28	0.16
12.8		163.84		9139.2	698.7	13186.69		0.68	0.0214
9.9		98.01			1156.13	123318.03	569.72	4.31	0.0202
12.2		148.84		10382.2	793.34	491.36	3324.31	0.0506	0.0678
12.5		156.25		9737.5	746.02	2483.36	1087.48	0.28	0.0423
					667.16	41548.03	1777.13	1.05	0.0674
10.5		110.25		10510.5	1061.49	29641.36	3659.15	2.18	0.0604
143.7		1733.23		117143.9		335387.67	26315.88	12.42	0.57

 

 

Поделиться:

Воспользуйтесь поиском по сайту: