 |
Задания для самостоятельного решения
|
|
|
|
Предел функции
Пусть функция  определена на некотором промежутке X и пусть точка
определена на некотором промежутке X и пусть точка 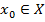 или
или  . Составим из множества X последовательность точек:
. Составим из множества X последовательность точек:  сходящихся к
сходящихся к  . Значения функции в этих точках также образуют последовательность:
. Значения функции в этих точках также образуют последовательность: 
Ø Число A называется пределом функции  в точке
в точке  , если для любой сходящейся к
, если для любой сходящейся к  последовательность значений аргумента
последовательность значений аргумента  , соответствующая последовательность значений функций сходится к числу A.
, соответствующая последовательность значений функций сходится к числу A.
Это описывает так: 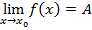 .
.
Односторонние (левый и правый)
Пределы функции
Левый предел – это односторонний предел функции, когда последовательность значений аргумента  слева от точки
слева от точки  , т.е.
, т.е.  .
.
Символическая запись левого предела функции:
 .
.
Правый предел – это односторонний предел функции, когда последовательность значений аргумента  справа от точки
справа от точки  , т.е.
, т.е.  .
.
Символическая запись левого предела функции:
 .
.
Теорема. Функция  имеет в точке
имеет в точке  предел тогда и только тогда, когда в этой точке существуют левый и правый пределы, и они равны. В таком случае предел функции равен односторонним пределам.
предел тогда и только тогда, когда в этой точке существуют левый и правый пределы, и они равны. В таком случае предел функции равен односторонним пределам.
WПример 2.15
Предел многочлена 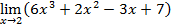 равен …
равен …
Варианты ответов: 1) 11; 2) 49; 3) 0; 4) 57.
Решение:
Для вычисления предела многочлена при  надо вместо переменной x подставить значение
надо вместо переменной x подставить значение  , к которому она стремится, и подсчитать, используя соответствующие теоретические положения.
, к которому она стремится, и подсчитать, используя соответствующие теоретические положения.
 .
.
WПример 2.16
Предел функции  равен …
равен …
Варианты ответов: 1)0; 2)1,5; 3)2; 4)  .
.
Решение:
Используем теоремы 5 и 3 о пределе отношения и пределе суммы, а затем подставим  в формулу дроби.
в формулу дроби.

WПример 2.17
Предел отношения двух многочленов  равен …
равен …
Решение:
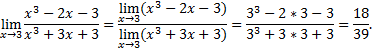
WПример 2.18
Предел дроби 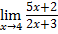 равен …
равен …
Варианты ответов: 1)1; 2)2; 3)0; 4)  .
.

Часто встречаются случаи, когда непосредственно нельзя применить теорему о пределе частного. Это так называемые неопределённости вида 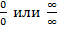 .
.
|
|
|
В ситуации, когда числитель и знаменатель дроби стремится к нулю. Тогда говорят, что имеет место неопределённость вида  . Для раскрытия неопределённости такого вида надо числитель и знаменатель разложить на множители.
. Для раскрытия неопределённости такого вида надо числитель и знаменатель разложить на множители.
Если числитель неограниченно возрастают при  , то в таком случае имеет место неопределённость вида
, то в таком случае имеет место неопределённость вида  . Для её раскрытия надо разделить числитель и знаменатель дроби на старшую степень
. Для её раскрытия надо разделить числитель и знаменатель дроби на старшую степень  .
.
WПример 2.19
Предел дроби 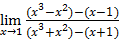 равен …
равен …
Решение:
Здесь имеет место неопределённость вида  . Это можно видеть, подставив
. Это можно видеть, подставив  . Для решения разложим на множители числитель, и знаменатель дроби, сократим общий множитель, после чего уже подставим предельное значение
. Для решения разложим на множители числитель, и знаменатель дроби, сократим общий множитель, после чего уже подставим предельное значение  :
:

WПример 2.20
Предел дроби 
 равен …
равен …
Решение:
Это неопределённость вида  . Разделим числитель и знаменатель на старшую степень
. Разделим числитель и знаменатель на старшую степень 

WПример 2.21
Предел дроби 
 равен …
равен …
Варианты ответов: 1)  ; 2)
; 2)  ; 3)0; 4)3.
; 3)0; 4)3.
Решение:
Разделим числитель и знаменатель на  (неопределённость вида
(неопределённость вида  ).
).

 3.
3.
WПример 2.22
Предел дроби 
 равен …
равен …
Варианты ответов: 1)0; 2)2; 3)-1; 4)1.
Решение:
Если непосредственно подставить в формулу  , то получим неопределённость вида
, то получим неопределённость вида  . Разложим числитель и знаменатель (а это квадратные трёхчлены) на множители, и сократим общий множитель.
. Разложим числитель и знаменатель (а это квадратные трёхчлены) на множители, и сократим общий множитель.



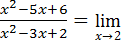
 -1.
-1.
WПример 2.23
Предел функции 
 равен …
равен …
Варианты ответов: 1)1; 2)2; 3)3; 4)4.
Решение:
Это непосредственность вида  – и числитель, и знаменатель дроби стремятся к нулю. Разложим и числитель и знаменатель для раскрытия неопределённости, и применим теорему о пределе частного и пределе суммы.
– и числитель, и знаменатель дроби стремятся к нулю. Разложим и числитель и знаменатель для раскрытия неопределённости, и применим теорему о пределе частного и пределе суммы.



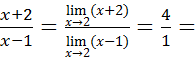 4.
4.
WПример 2.24
Предел функции 
 равен …
равен …
Варианты ответов: 1)0; 2)1; 3)2; 4)8.
Решение:
Покажем это. Это неопределённость вида  , так как и числитель, и знаменатель стремятся к
, так как и числитель, и знаменатель стремятся к  при
при  . Разделим их на
. Разделим их на  и применим теорему о пределе частного, которую до этого применять было нельзя.
и применим теорему о пределе частного, которую до этого применять было нельзя.
|
|
|


 1.
1.
WПример 2.25
Предел функции 
 равен …
равен …
Варианты ответов: 1)0; 2)2; 3)4; 4)8.
Решение:
Это неопределённость вида  . Разделим числитель и знаменатель на
. Разделим числитель и знаменатель на  и применим теорему о пределе частного, а затем теорему о пределе суммы.
и применим теорему о пределе частного, а затем теорему о пределе суммы.


 4.
4.
WПример 2.26
Предел дроби 
 равен …
равен …
Решение:
Так как это неопределённость вида  , то разделим и числитель, и знаменатель на
, то разделим и числитель, и знаменатель на  , после чего воспользуемся теоремой о пределе частного.
, после чего воспользуемся теоремой о пределе частного.


 0.
0.
Рассмотрим раскрытие неопределённость вида  -
-  . Для этого умножим и разделим данное выражение на сопряжённое, после чего используем приём, рассмотренный выше: разделим и числитель, и знаменатель на старшую степень переменной
. Для этого умножим и разделим данное выражение на сопряжённое, после чего используем приём, рассмотренный выше: разделим и числитель, и знаменатель на старшую степень переменной  .
.
WПример 2.27
Предел функции  равен …
равен …
Решение:
Умножим на сопряжённое выражение  и разделим на него.
и разделим на него.

Теперь разделим и числитель и знаменатель на  .
.
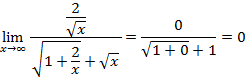
Задания для самостоятельного решения
44. 
 ; 45.
; 45. 
 ;
;
46. 
 ; 47.
; 47. 
 ;
;
48. 
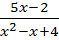 ; 49.
; 49. 
 ;
;
50. 
 ; 51.
; 51. 
 ;
;
52. 
 ; 53.
; 53. 

54. 
 55.
55.  ;
;
|
|
|


