 |
Прохождение случайных сигналов через линейные инерционные цепи
|
|
|
|
Рассмотрим линейную инерционную систему с известной передаточной функцией 
или импульсной реакцией 
. Пусть на вход такой системы поступает стационарный случайный процесс с заданными характеристиками: плотностью вероятности 
, корреляционной функцией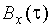 
или энергетическим спектром 
. Определим характеристики процесса 
на выходе системы: 
, 
и 
.
Наиболее просто можно найти энергетический спектр процесса на выходе системы. Действительно, отдельные реализации процесса на входе являются детерминированными
функциями, и к ним применим аппарат Фурье. Пусть 
- усеченная реализация длительности Т случайного процесса на входе, а
(3.4.1)
- ее спектральная плотность. Спектральная плотность реализации 
на выходе линейной системы будет равна
(3.4.2)
Энергетический спектр процесса на выходе согласно (3.3.3) будет определиться выражением
(3.4.3)
т.е. будет равен энергетическому спектру процесса на входе, умноженному на квадрат амплитудно-частотной характеристики системы, и не будет зависеть от фазочастотной характеристики.
Корреляционная функция процесса на выходе линейной системы может быть определена как преобразование Фурье от энергетического спектра:
(3.4.4)
Следовательно, при воздействии случайного стационарного процесса на линейную систему на выходе получается также стационарный случайный процесс с энергетическим спектром и корреляционной функцией, определяемыми выражениями (3.4.3) и (3.4.4). Мощность процесса на выходе системы будет равна
(3.4.5)
Плотность распределения вероятности и числовые характеристики сигнала на выходе безынерционной нелинейной цепи.
Баскаков стр. 300 – 302
Прохождение случайных сигналов через нелинейные безинерционные цепи.
|
|
|
Рассмотрим теперь задачу о прохождении случайного процесса через нелинейную систему. В общем случае эта задача весьма сложная, но она значительно упрощается, когда нелинейная система является безынерционной. В безынерционных нелинейных системах значения выходного процесса 
в данный момент времени определяются значениями входного процесса в тот же самый момент времени. Для нелинейных безынерционных преобразований более простой задачей является определение функций распределения на выходе в гораздо более сложной – определение корреляционной функции или энергетического спектра.
Как отмечалось выше, n - мерная функция распределения случайного процесса по сути дела является функцией распределения n случайных величин, представляющих собой значения случайного процесса в n различных моментов времени, Определение законов распределения функционально преобразованных случайных величин является сравнительно простой задачей.
Рассмотрим простейший пример одномерной случайной величины. Пусть 
- плотность вероятности случайной величины ζ, которая подвергается нелинейному преобразованию 
. Определим плотность вероятности 
случайной величины η. Предположим, что функция такова, что обратная ей функция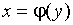 
– однозначна.
Если случайная величина ζ находится в достаточно малом интервале 
, то вследствие однозначной функциональной зависимости между ζ и η случайная величина η обязательно будет находиться в интервале 
, где 
, вероятности этих событий должны быть одинаковыми, т.е. 
(3.4.13)
откуда находим
(3.4.14)
Производная в последнем выражении берется по абсолютной величине, так как плотность вероятности не может быть отрицательной. Если обратная функция 
неоднозначная, т.е. имеет несколько ветвей 
, то для плотности вероятности с использованием теоремы сложения вероятностей можно получить
|
|
|
(3.4.15)
Отметим, что для определения числовых характеристик нелинейно-преобразованных случайных процессов нет необходимости определять их плотности вероятностей. Действительно, в общем случае для начального момента k-го порядка имеем
(3.4.16)
Но согласно (3.4.13) 
и . Поэтому последнее выражение можно переписать
(3.4.17)
Полученные выражения (3.4.14) и (3.4.15) легко распространить на случай нескольких величин. Приведем здесь лишь окончательный результат для двумерного случая. Если случайные величины 
и 
имеют совместную плотность вероятностей 
, то для случайных величин
(3.4.18)
при однозначности обратных функций
совместная плотность вероятностей будет определяться выражением
где величина
называется якобианом преобразования и представляет собой отношение элементарных площадей 
при переходе от одной системы координат к другой. Если 
, то справедливо равенство
где 
Вопрос № 23
Дискретная импульсная последовательность, их спектр.
Баскаков стр. 382-383
Дискретизация периодических сигналов. Дискретное преобразование Фурье (ДПФ). Восстановление исходного сигнала по ДПФ. Обратное дискретное преобразование Фурье (ОДПФ).
Баскаков стр. 388-392
Вопрос № 24
Принцип цифровой обработки (ЦО) сигналов на основе дискретного преобразования Фурье.
Баскаков стр. 400-405
Реализация алгоритмов цифровой фильтрации (трансверсальные ЦФ, рекурсивные ЦФ, импульсная характеристика, сигнал на выходе)
Цифровые фильтры в зависимости от обратной связи бывают рекурсивные (РФ) и нерекурсивные (НФ).
Преимущества нерекурсивных фильтров по сравнению с рекурсивными сводятся к следующему:
- нерекурсивные фильтры могут иметь точно линейную ФЧХ;
- мощность собственных шумов НФ, как правило, гораздо меньше, чем у РФ;
- для НФ проще вычисление коэффициентов.
Недостатки нерекурсивных фильтров по сравнению с рекурсивными сводятся к следующему:
- рекурсивные фильтры позволяют производить обработку сигнала с более высокой точностью, так как они позволяют более правильно реализовать импульсную характеристику без отбрасывания ее «хвоста»;
- схемная реализация РФ намного проще, чем у НФ;
|
|
|
- рекурсивные фильтры позволяют реализовать алгоритмы, вообще не- реализуемые с помощью нерекурсивных фильтров.
Импульсная характеристика рекурсивного фильтра бесконечная, а нерекурсивного конечная.
Баскаков стр. 405-408, 409-411, 413
Вопрос №25
Понятие отношения сигнал/шум, фильтрации и оптимального фильтра.
Отношение сигнал/шум — безразмерная величина, равная отношению мощности полезного сигнала к мощности шума.
Фильтрация — это процесс обработки сигнала частотно-избирательными устройствами с целью изменения спектрального состава сигнала.
Оптимальным линейным фильтром называют частотно-избирательную систему, выполняющую обработку суммы сигнала и шума некоторым наилучшим образом. На выходе максимизирует отношение сигнал/шум.
Баскаков стр. 423-424
Отношение сигнал/шум на выходе согласованного фильтра.
Баскаков стр. 425, 431-432
Характеристики оптимального (согласованного) фильтра для сигналов известной формы (АЧХ, ФЧХ, ИХ).
Сигнал на выходе согласованного фильтра.
|
|
|
