 |
Обнаружение взаимоблокировки при наличии одного ресурса каждого типа
|
|
|
|
Под одним ресурсом каждого типа, подразумевается один принтер, один сканер и один плоттер и т.д.
Рассмотрим систему из 7-ми процессов и 6-ти ресурсов.

Обнаружение взаимоблокировки при наличии одного ресурса каждого типа
Визуально хорошо видна взаимоблокировка, но нам нужно чтобы ОС сама определяла взаимоблокировку.
Для этого нужен алгоритм.
Рассмотрим один из алгоритмов.
Для каждого узла N в графе выполняется пять шагов.
1. Задаются начальные условия: L-пустой список, все ребра не маркированы.
2. Текущий узел добавляем вконец списка L и проверяем количество появления узла в списке. Если он встречается два раза, значит цикл и взаимоблокировка.
3. Для заданного узла смотрим, выходит ли из него хотя бы одно немаркированное ребро. Если да, то переходим к шагу 4, если нет, то переходим к шагу 5.
4. Выбираем новое немаркированное исходящее ребро и маркируем его. И переходим по нему к новому узлу и возвращаемся к шагу 3.
5. Зашли в тупик. Удаляем последний узел из списка и возвращаемся к предыдущему узлу. Возвращаемся к шагу 3. Если это первоначальный узел, значит, циклов нет, и алгоритм завершается.
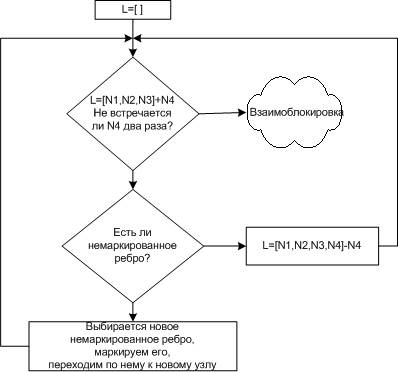
Алгоритм обнаружения взаимоблокировок
Для нашего случая тупик обнаруживается в списке L=[B,T,E,V,G,U,D,T]
Обнаружение взаимоблокировки при наличии нескольких ресурсов каждого типа
Рассмотрим систему.
m - число классов ресурсов (например: принтеры это один класс)
n - количество процессов
P(n) - процессы
E - вектор существующих ресурсов
E(i) - количество ресурсов класса i
A - вектор доступных (свободных) ресурсов
A(i) - количество доступных ресурсов класса i
С - матрица текущего распределения (какому процессу, какие ресурсы принадлежат)
|
|
|
R - матрица запросов (какой процесс, какой ресурс запросил)

C(ij) - количество экземпляров ресурса j, которое занимает процесс P(i).
R(ij) - количество экземпляров ресурса j, которое хочет получить процесс P(i).

Общее количество ресурсов равно сумме занятых и свободных ресурсов
Рассмотрим алгоритм поиска тупиков.
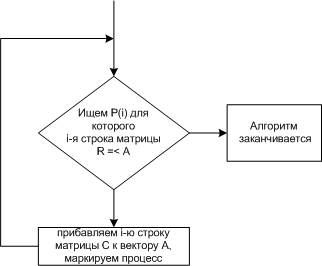
Алгоритм поиска тупиков при наличии нескольких ресурсов каждого типа
Если остаются не маркированные процессы, значит, есть тупик.
Рассмотрим работу алгоритма на реальном примере.
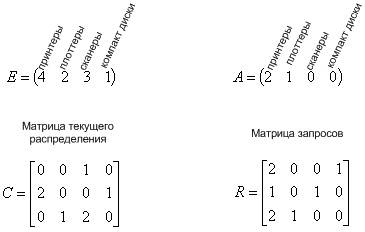
Используем алгоритм:
1. Третий процесс может получить желаемые ресурсы, т.к. R (2 1 0 0) = A (2 1 0 0)
2. Третий процесс освобождает ресурсы. Прибавляем их к A. А = (2 1 0 0) + (0 1 2 0) =(2 2 2 0). Маркируем процесс.
3. Может выполняться процесс 2. По окончании А=(4 2 2 1).
4. Теперь может работать первый процесс.
Тупиков не обнаружено.
Если рассмотреть пример, когда второму процессу требуются ресурсы (1 0 3 0), то два процесса окажутся в тупике.
Когда можно искать тупики:
· Когда запрашивается очередной ресурс (очень загружает систему)
· Через какой то промежуток времени (в интерактивных системах пользователь это ощутит)
· Когда загрузка процессора слишком велика
Выход из взаимоблокировки
Восстановление при помощи принудительной выгрузки ресурса
Как правило, требует ручного вмешательства (например: принтер).
Восстановление через откат
Состояние процессов записывается в контрольных точках, и в случае тупика можно сделать откат процесса на более раннее состояние, после чего он продолжит работу снова с этой точки.
С принтером опять будут проблемы.
Восстановление путем уничтожения процесса
Самый простой способ.
Но с принтером опять будут проблемы.
В реальных системах они не годятся.
Динамическое избежание взаимоблокировок
В этом способе ОС должна знать, является ли предоставление ресурса безопасным или нет.
Траектории ресурсов
|
|
|
Рассмотрим модель из двух процессов и двух ресурсов.
А1 - запрос принтера процессом А
А2 - запрос плоттера процессом А
А3 - освобождение принтера процессом А
А4 - освобождение плоттера процессом А
В1 - запрос плоттера процессом В
В2 - запрос принтера процессом В
В3 - освобождение плоттера процессом В
В4 - освобождение принтера процессом В
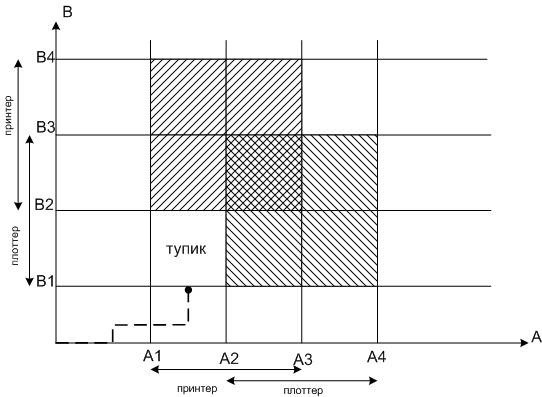
Динамическое избежание взаимоблокировок
Т.к. процессор предоставляется поочередно, траектория может продолжаться только параллельно осям.
Чтобы избежать тупика, процессам надо обойти прямоугольник, охватывающий всю заштрихованную область.
|
|
|


