 |
Примерный перечень вопросов выносимых на зачет
|
|
|
|
Методические указания к решению задач
2.1. При решении задачи 1 необходимо:
1) Найти итоговые значения показателя, по каждому году изучаемого периода и записать их вместо знака «?».
2) Рассчитать доли каждой группы, выделенной в составе явления.
3) Найти значения коэффициента Гатева, характеризующие структурные различия, за два периода по формуле:
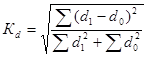 ,
,
где d1,d0 - доли каждой из частей совокупности в отчетном и базисном периодах. Показатели доли рассчитываются как отношение части к общему и выражаются в %.
Коэффициент Гатева принимает значения в пределах от -1 до 1. Если значение коэффициента больше чем 0,2, то структурные различия считаются значительными.
Пример решения задачи 1.
Имеются следующие данные о структуре ВВП региона по видам первичных доходов, млрд.руб. (в фактически действовавших ценах, %.)
Таблица 2.1 - Расчет показателей структуры
| d00, % | d06,% | d12.% | ||||
| Официальная оплата труда наемных работников | 1351.0 | 3614.9 | 5406.1 | 35,0 | 37,9 | 40,2 |
| Скрытая оплата труда наемных работников | 347.4 | 1106.4 | 1707.9 | 9,0 | 11,6 | 12,7 |
| Чистые налоги на производство и импорт | 401.4 | 925.2 | 10,4 | 9,7 | 9,6 | |
| Валовая прибыль экономики | 1760.2 | 3891.5 | 45,6 | 40,8 | 37,5 | |
| Итого ввп | 3860,0 | 100,0 | 100,0 | 100,0 |
 *100
*100

Таблица 2.2 - Расчет интегральных коэффициентов структурных сдвигов
| d00 | d06 | d12 | d06-d00 | d12-d06 | (d06-d00)2 | (d12-d06)2 | (d00)2 | (d06)2 | (d12)2 | |
| Официальная оплата труда наемных работников | 35,0 | 37,9 | 40,2 | 2,9 | 2,3 | 8,4 | 5,3 | 1225,0 | 1436,4 | 1616,0 |
| Скрытая оплата труда наемных работников | 9,0 | 11,6 | 12,7 | 2,6 | 1,1 | 6,8 | 1,2 | 81,0 | 134,6 | 161,3 |
| Чистые налоги на производство и импорт | 10,4 | 9,7 | 9,6 | -0,7 | -0,1 | 0,5 | 0,0 | 108,2 | 94,1 | 92,2 |
| Валовая прибыль | 45,6 | 40,8 | 37,5 | -4,8 | -3,3 | 23,0 | 10,9 | 2079,4 | 1664,6 | 1406,3 |
| Итого | 100,0 | 100,0 | 100,0 | Х | Х | 38,7 | 17,4 | 3493,5 | 3329,7 | 3275,7 |
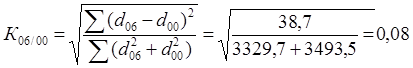 ;
;
|
|
|
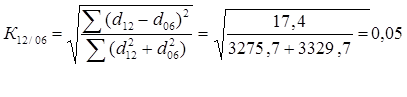
Сравнение коэффициентов между собой показывает, что более интенсивные структурные сдвиги произошли в 2000-2006гг. (К06/00>К12/06). В то же время, поскольку значения коэффициентов близки к 0, можно говорить о незначительном изменении структуры.
2.2. При решении задачи 2 необходимо рассчитать средние значения показателя, выбрав правильно формулу для расчета средней величины. Для этого необходимо:
1) Определить вид осредняемого признака первичный или вторичный (первичный признак – это абсолютная величина, выраженная в натуральных, стоимостных или трудовых единицах измерения; вторичный признак – результат соотношения значений двух первичных признаков, выраженный сложными единицами измерения (например, производительность труда – руб./чел.)
Для первичных признаков расчет среднего значения выполняется по схеме простой средней арифметической.
Для вторичных признаков, необходимо выяснить схему расчета индивидуальных значений осредняемого признака, используя буквенные обозначения, т.е. записать логическую формулу средней величины.
Если имеющаяся в условии задачи информация такова, что в формуле логической средней неизвестен числитель, то применяется средняя арифметическая взвешенная, а, если знаменатель - средняя гармоническая взвешенная.
Пример решения задачи 2.
Для трех крупных предприятий одного из районов города известны следующие данные:
Таблица 2.3-Данные для расчета средней величины
| Предприятия | Численность рабочих, чел. (Ч) | Производительность труда 1 работника, тыс. руб. на 1 человека (В) |
Определите среднюю производительность труда по району. Укажите вид и форму средней величины.
Решение.
1)Производительность труда – вторичный признак, представляющий собой соотношение стоимости произведенной продукции и численности работников.
|
|
|
Логическая формула:
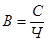 , где стоимость произведенной продукции.
, где стоимость произведенной продукции.
2) По условию задачи неизвестна стоимость произведенной продукции, то есть числитель логической формулы, значит расчет средней производительности труда проводим по схеме средней арифметической взвешенной.
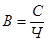 ; С –неизвестна.
; С –неизвестна.
Выражаем С через известные признаки: С =В*Ч. Подставим это выражение в исходное равенство:
Получим:
- для одного предприятия 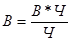 ;
;
-для совокупности предприятий: 
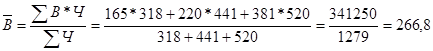 тыс.руб. на 1 чел.
тыс.руб. на 1 чел.
Средняя производительность труда 2 работника по району города составила в среднем 266,8 тыс.руб. на 1 чел. При расчете использована средняя арифметическая взвешенная.
2.3. При решении задачи 3 необходимо:
1) Перейти от интервального ряда к дискретному, рассчитав середины интервалов как полусуммы границ.
2) Рассчитать накопленную частоту (Fi) по каждому интервалу, равную сумме частот всех предшествующих интервалов, включая данный.
3) Графически изобразить интервальный вариационный ряд в виде ряда прямоугольников, построенных на оси Х. Их ширина равна длине интервала, а высота соответствующей частоте. Такой график называется гистограммой распределения. Если середины верхних сторон прямоугольников соединить прямыми, то можно получить полигон распределения, площадь которого соответствует площади гистограммы.
4) Рассчитать среднее значение интервального ряда по формуле:
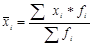 , где хi- середина интервала, fi- частота интервала.
, где хi- середина интервала, fi- частота интервала.
5) Вычислить моду и медиану, характеризующие центр изучаемого распределения по следующим формулам:
Мода: 
где:
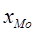 - нижняя граница модального интервала (интервала с наибольшей частотой),
- нижняя граница модального интервала (интервала с наибольшей частотой),
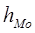 - длина модального интервала
- длина модального интервала
 - частота интервала, соответственно предшествующего модальному, модального и следующего за модальным.
- частота интервала, соответственно предшествующего модальному, модального и следующего за модальным.
Медиана: 
где:
 - нижняя граница медианного интервала. У медианного интервала кумулятивная частота равна или превышает половину суммы частот.
- нижняя граница медианного интервала. У медианного интервала кумулятивная частота равна или превышает половину суммы частот.
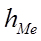 - длина медианного интервала
- длина медианного интервала
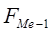 - накопленная частота, предшествующая медианному интервалу.
- накопленная частота, предшествующая медианному интервалу.
 -сумма всех частот.
-сумма всех частот.
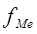 -частота медианного интервала.
-частота медианного интервала.
6) Рассчитать показатели вариации, характеризующие разброс значений изучаемого признака вокруг средней величины по следующим формулам:
|
|
|
Таблица 2.4 - Формулы для расчета показателей вариации
| Показатель | Формула |
| Среднее линейное отклонение | 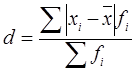
|
| Дисперсия | 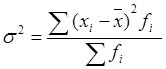
|
| Среднее квадратическое отклонение | 
|
| Коэффициент вариации | 
|
где:
хi- середина интервала,
fi- частота интервала
Если значение коэффициента вариации не превышает 50%, то вариация значений находится в пределах нормы. Если оно составляет более 50%, то совокупность неоднородна, средняя не надежна, необходимо с помощью типологической группировки выделять частные совокупности и изучать вариацию внутри данных групп.
7) Рассчитать коэффициент асимметрии, характеризующий форму распределения изучаемого признака по формуле Пирсона:
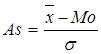
Пример решения задачи 3.
Таблица 2.5- Расчет показателей вариации
| Группы рабочих по оплате труда, тыс.руб. | Число рабочих, чел. (f) | Накопленная частота, (F) | Середина интервала (xi) | xi * f | 
| | 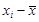 | * f | * f
| (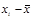 )2 )2
| (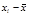 )2 * f )2 * f
| |
| До 4 | 2,0 | 18,0 | -7,3 | 65,70 | 53,29 | 479,61 | |||
| 4-8 | 6,0 | 90,0 | -3,3 | 49,50 | 10,89 | 163,35 | |||
| 8-12 | 10,0 | 290,0 | 0,7 | 20,30 | 0,49 | 14,21 | |||
| 12-16 | 14,0 | 182,0 | 4,7 | 61,10 | 22,09 | 287,17 | |||
| 16 и более | 18,0 | 72,0 | 8,7 | 34,80 | 75,69 | 302,76 | |||
| Итого | х | х | 652,0 | х | 231,40 | 162,45 | 1247,10 | ||
1.Средняя заработная плата: 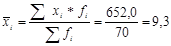 тыс.руб.
тыс.руб.
2.Показатели вариации:
а) Размах вариации: 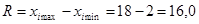 тыс.руб.
тыс.руб.
б) Среднее линейное отклонение: 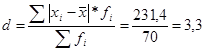 тыс.руб.
тыс.руб.
В среднем индивидуальные значения показателя оплаты труда отклоняются от своего среднего значения на 3,3 тыс.руб.
в) Дисперсия 
г)Среднее квадратическое отклонение: 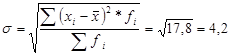 тыс.руб.
тыс.руб.
В среднем индивидуальные значения показателя оплаты труда отклоняются от своего среднего значения на 4,2 тыс.руб.
д) Коэффициент вариации:  %;
%;
Вариация в пределах нормы (V≤50%). Средняя надежна
3) Мода: 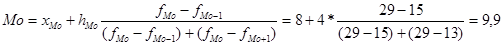 тыс.руб.
тыс.руб.
где:
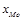 - нижняя граница модального интервала (интервала с наибольшей частотой, f).
- нижняя граница модального интервала (интервала с наибольшей частотой, f).
Модальный интервал для рассматриваемой задачи: 8-12, так как ему соответствует максимальная частота (29).
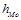 - длина модального интервала (в примере hMo=12-8=4)
- длина модального интервала (в примере hMo=12-8=4)
|
|
|
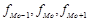 - частота интервала, соответственно предшествующего модальному, модального и следующего за модальным.
- частота интервала, соответственно предшествующего модальному, модального и следующего за модальным.
В рассматриваемой совокупности наиболее часто встречается значение оплаты труда, равное 9,9 тыс. руб.
4)Медиана:  тыс.руб.
тыс.руб.
где:
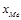 - нижняя граница медианного интервала. У медианного интервала кумулятивная частота равна или превышает половину суммы частот. 70/2=35 Интервал, у которого F>35 и будет медианным. (от 8 до 12 тыс.руб.)
- нижняя граница медианного интервала. У медианного интервала кумулятивная частота равна или превышает половину суммы частот. 70/2=35 Интервал, у которого F>35 и будет медианным. (от 8 до 12 тыс.руб.)
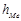 - длина медианного интервала
- длина медианного интервала
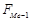 - накопленная частота, предшествующая медианному интервалу. (9+15=24)
- накопленная частота, предшествующая медианному интервалу. (9+15=24)
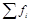 -сумма всех частот. (70)
-сумма всех частот. (70)
 -частота медианного интервала. (29).
-частота медианного интервала. (29).
В рассматриваемой совокупности оплата труда 50% работников составляет сумму менее 9,5 тыс.руб.., а у остальных 50% - более 9,5 тыс. руб.
5) Коэффициент асимметрии (As):  , асимметрия левосторонняя, незначительная, т.е. средняя, вычисленная по совокупности достаточно надежна.
, асимметрия левосторонняя, незначительная, т.е. средняя, вычисленная по совокупности достаточно надежна.
Если As>0,5- асимметрия значительна.
2.4. При решении задачи 4 необходимо воспользоваться формулами средней и предельной ошибок выборки, для ответа на один из трех вопросов, соответствующих трем типам задач:
1) Каковы границы доверительного интервала для средней (для доли) изучаемого признака?
2) С какой вероятностью можно гарантировать заданные результаты?
3) Сколько единиц нужно обследовать, чтобы предельная ошибка выборки не превысила заданной величины?
В ходе решения необходимо воспользоваться формулами средней ошибки выборки для повторного и бесповторного отбора:
Таблица 2.6 - Формулы расчета средней ошибки выборки при простом случайном отборе:
| Повторный | Бесповторный | |
| Для средней | 
| 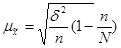
|
| Для доли | 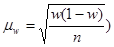
| 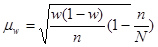
|
Таблица 2.7 - Формулы для нахождения необходимой численности выборки при простом случайном отборе.
| Повторный | Бесповторный | |
| Для средней | 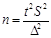
| 
|
| Для доли | 
| 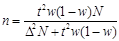
|
Примеры решения задачи 4:
Типовая задача 4.1
На предприятии проводится изучение внутрисменных потерь рабочего времени. Из 3675 рабочих предприятия в порядке бесповторной выборки обследован 441 человек. Установлено, что в среднем за день потери составили 24 мин. при среднем квадратическом отклонении 16 мин. выявлены они были у 265 человек из числа обследованных. С вероятностью 0, 954 необходимо определить возможные пределы внутрисменных потерь рабочего времени и доли рабочих, допустивших внутрисменные потери.
| Дано | Решение |
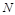 =3675 =3675
| 1) 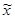 =24 мин. Необходимо определить =24 мин. Необходимо определить 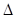 : :
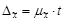
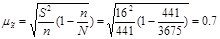 мин. мин.
 , так как F(t)= 0,954 , так как F(t)= 0,954
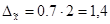 мин.
Пределы внутрисменных потерь рабочего времени составят: мин.
Пределы внутрисменных потерь рабочего времени составят:
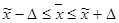 ; 24,0-1,4≤ ; 24,0-1,4≤ 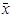 ≤24,0+1,4; 22,6≤ ≤24,0+1,4; 22,6≤ 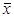 ≤25,4
2)w=0.6 Необходимо определить ≤25,4
2)w=0.6 Необходимо определить 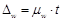
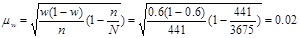  , так как F(t)= 0,954 , так как F(t)= 0,954
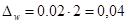 Пределы доли работников, допустивших внутрисменные перерывы, составят:
Пределы доли работников, допустивших внутрисменные перерывы, составят:
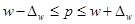 , 0.60.04≤р≤0,6+0,04; 0.56≤р≤0,64 , 0.60.04≤р≤0,6+0,04; 0.56≤р≤0,64
|
| n=441 | |
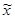 =24 =24
| |
| S=16 | |
| |
| F(t)=0,954 | |
1)  –?
2) –?
2)  -? -?
|
|
|
|
Типовая задача 4.2.
Для определения качества профессиональной подготовки студентов-выпускников проводится их выборочная аттестация. С этой целью из 5200 студентов обследуется каждый десятый студент. Средний балл аттестации по выборке составил 4,23, а среднее квадратическое отклонение составило 0,930. С какой вероятностью можно утверждать, что средний балл аттестации для всех студентов не превысит 4,31 и будет не ниже 4,15.
| Дано | Решение |
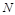 =5200 =5200
| Чтобы найти вероятность того, что средний балл не выйдет за указанные границы, необходимо найти t – коэффициент доверия: t определяем исходя из предельной ошибки выборки:  Нам известны границы доверительного интервала и средняя величина.
Отсюда
Нам известны границы доверительного интервала и средняя величина.
Отсюда
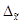 = = 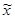 – ( – (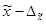 )= 4,23–4,15 = 0,08 )= 4,23–4,15 = 0,08
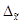 =( =( ) - ) -  =4,31-4,23=0,08
Далее необходимо рассчитать: =4,31-4,23=0,08
Далее необходимо рассчитать: 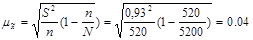 мин. мин.
 ; F(t)=0,954
С вероятностью 0,954 средний балл аттестации для всех студентов не превысит 4,31 и будет не ниже 4,15. ; F(t)=0,954
С вероятностью 0,954 средний балл аттестации для всех студентов не превысит 4,31 и будет не ниже 4,15.
|
| n=520 | |
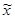 =4.23 =4.23
| |
| S=0.93 | |
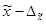 =4,15 =4,15
 =4,31 =4,31
| |
| F(t)-? |
Типовая задача 4.3.
Поставлена задача определения урожайности зерновых культур, под которыми в регионе засеяны 3000 га. В предварительном исследовании установлено, что при средней урожайности зерновых 25 ц. с 1га, коэффициент вариации урожайности составил 18%. Предельная ошибка средней урожайности в будущем исследовании не должна превышать 0,4 ц. с 1га с вероятностью 0,954. Следует рассчитать, на скольких гектарах посевов должен быть проведен бесповторный выборочный учет урожайности зерновых культур, чтобы обеспечить требуемую точность результатов.
| Дано | Решение |
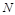 =3000 =3000
| Численность выборки для бесповторного случайного отбора определяется как:
 S – среднее квадратическое отклонение по выборке находим из формулы коэффициента вариации:
S – среднее квадратическое отклонение по выборке находим из формулы коэффициента вариации:  , тогда , тогда 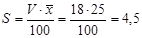 ц с 1 га
Так как F(t)=0,954, t=2 ц с 1 га
Так как F(t)=0,954, t=2
 га га
|
2.5. Пример решения задачи 5.
Имеются следующие данные (гр.1,2,3):
| № завода | Основные производственные фонды, (Х) | Валовой выпуск продукции, млн.руб., (Yi) | 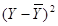
| Rx | Ry | d = Rx- Ry | d2 |
| 1. | |||||||
| 2. | -1 | ||||||
| 3. | |||||||
| 4. | |||||||
| 5. | |||||||
| 6. | -1 | ||||||
| 7. | |||||||
| 8. | |||||||
| 9. | |||||||
| 10. | |||||||
| Итого | х | х | х |
Требуется провести однофакторную аналитическую группировку результата с фактором,
найти показатели тесноты связи по аналитической группировке и коэффициент корреляции рангов Спирмена.
Решение
Порядок проведения аналитической группировки:
1)определяем: какой из признаков является фактором (Х), т.е. причиной, а какой результатом (Y), т.е. следствием
2)проводим ранжирование данных по возрастанию (по признаку-фактору).
3)строим группировку с равными интервалами по признаку фактору. Число интервалов определяется по правилу Стерджесса или опытным путем. При небольшом числе единиц (до 30) достаточно 3-4 интервала.
Величина интервала рассчитывается как (xmax –xmin)/кол-во интервалов. Границы интервалов округляются до целого числа.
4)заполняем графы полученной группировки: 1-я графа–интервалы по признаку-фактору, 2-я графа–число предприятий попавших в каждую группу, 3-я графа–сумма значений признака Y по каждой группе, 4-я графа – среднее значение Y по группе, 5-я графа – отклонения среднего значения по группе от среднего значения по совокупности, 6-я графа – отклонения в квадрате, 7-я графа– отклонения в квадрате, умноженные на частоту в гр.2
| Основные производственные фонды, Х | fi ед | ВВ по группе, млн.руб. ∑Yi | ВВ в среднем по группе, 
| 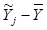
| 
| 
|
| 4=3:2 | 5=4- 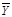
| 6=52 | 7=6*2 | |||
| 12-42 | 35,3 | -64,7 | 4181,8 | 12545,3 | ||
| 43-73 | 93,2 | -6,8 | 46,2 | 231,2 | ||
| 74-104 | 214,0 | 114,0 | 12996,0 | 25992,0 | ||
| Итого | х | х | 17228,3 | 38768,5 |
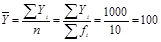 млн.руб. – средний объем валового выпуска в целом по совокупности
млн.руб. – средний объем валового выпуска в целом по совокупности
Тесноту связи характеризует эмпирическое корреляционное отношение:
 , где
, где 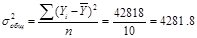 – общая дисперсия
– общая дисперсия
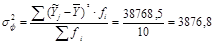 - факторная (межгрупповая) дисперсия
- факторная (межгрупповая) дисперсия

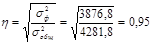 - η изменяется от 0 до 1, чем ближе η к 1,тем теснее связь.
- η изменяется от 0 до 1, чем ближе η к 1,тем теснее связь.
Теснота связи оценивается по следующей шкале:
До 0,3 – слабая
0,3-0,5 – умеренная
0,5-0,7 – заметная
0,7-0,9 – тесная
Св. 0,9 - очень тесная
Связь между объемом основных фондов и валовым выпуском тесная
Дополнительно рассчитывается коэффициент детерминации 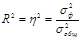 – показывает какая часть общей вариации признака Y объясняется вариацией признака-фактора Х. В нашем примере R2 = 0,9, то есть 90% вариации показателя валового выпуска определяется изменением объема основных фондов.
– показывает какая часть общей вариации признака Y объясняется вариацией признака-фактора Х. В нашем примере R2 = 0,9, то есть 90% вариации показателя валового выпуска определяется изменением объема основных фондов.
Теснота связи может быть также охарактеризована с помощью коэффициента ранговой корреляции Спирмена:
Коэффициент корреляции рангов основан на рассмотрении разности рангов значений признаков.
 , где n -число единиц совокупности, d- разность между знаками.
, где n -число единиц совокупности, d- разность между знаками. 
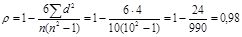 – связь прямая тесная.
– связь прямая тесная.
2.6. При решении задачи 6 необходимо оценить связь между качественными признаками по таблицам взаимной сопряженности с помощью коэффициентов ассоциации и контингенции
Пример решения задачи 6
| Население | Отношение к реформам | Всего | |
| положительное | отрицательное | ||
| городское | 150 (a) | 80 (b) | |
| сельское | 90 (c) | 120 (d) | |
| Всего |
 Для оценки тесноты связи между признаками рассчитывается коэффициент ассоциации:
Для оценки тесноты связи между признаками рассчитывается коэффициент ассоциации:
 =0,42
=0,42
Недостаток коэффициента ассоциации состоит в том, что если хотя бы один из четырех показателей будет отсутствовать, величина коэффициента ассоциации будет равна 1, что дает преувеличенную оценку степени тесноты связи между признаками.
В этом случае пользуются коэффициентом контингенции.
 =0,22
=0,22
Коэффициенты ассоциации и контингенции изменяются от –1(что означает обратную связь) до +1 (прямая связь). Чем ближе Кк к 1 или –1, тем сильнее связаны между собой признаки.
В нашем примере связь между признаками умеренная.
2.7. При решении задачи 7 необходимо:
1) По исходным данным установить взаимосвязь признаков.
При использовании индексов обычно предполагается наличие жёсткой мультипликативной связи признака-результата и признаков-факторов:
Например, зависимость товарооборота (W)- от физического объёма реализованных товаров разного вида (q)- и от цен за единицу товара каждого вида (p) -. Следует определить, какой из признаков данной системы отсутствует в условии задачи и рассчитать его значения в базисном и отчётном периодах. Если, например, отсутствует W, тогда W=p*q; если отсутствует q, тогда q=W/p; если отсутствует p, тогда p=W/q.
При этом символом q обозначается количественный показатель, представляющий собой первичный признак (количество товара, численность работников), символом p – качественный показатель, представляющий собой вторичный признак (цена, себестоимость, материалоемкость единицы продукции)
2) Рассчитать общие индексы в абсолютной и относительной формах.
В теории индексов применяется следующего правила построения индексов:
1) Индексы качественных показателей, анализирующих изменение вторичных признаков (цены за единицу товара, себестоимости единицы продукции, фондоотдачи, средней заработной платы), строятся с весами отчетного периода. Индекс, построенный на весах отчетного периода в теории статистики получил название индекса Пааше по имени автора, предложившего его.

2)Индексы количественных показателей, характеризующих изменение физических размеров явления (например, количество проданного товара, численность работающих, производство продукции в натуральном выражении), строятся с весами базисными весами. Индекс, построенный на весах базисного периода, называется индексом Ласпейреса.
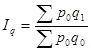
И для индивидуальных и для общих индексов действует общее правило: индексы связаны между собой так же, как и индексируемые величины. Например, товарооборот – это произведение цены на количество реализованного товара. Точно такая же зависимость выполняется для индексов этих показателей:
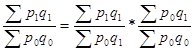

Систему индексов можно построить не только в относительной, но и в разностной форме, то есть определить абсолютное влияние каждого из факторов на изменение результативного показателя:
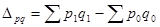 -общее изменение товарооборота.
-общее изменение товарооборота.
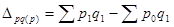 - изменение товарооборота под влиянием цен.
- изменение товарооборота под влиянием цен.
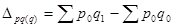 - изменение товарооборота под влиянием физического объема товарооборота.
- изменение товарооборота под влиянием физического объема товарооборота.
Пример решения задачи 7.
Имеются данные по проектным организациям города:
Таблица 2.8 - Данные для расчета индексных систем
в относительной и абсолютной форме
| Организации | Численность работников, чел. (q) | Фонд заработной платы, тыс.руб. (w) | Средняя заработная плата, тыс.руб. p=w/q | |||
| базисный | отчетный | базисный | отчетный | базисный | отчетный | |
| 638,4 | 840,0 | 5,6 | 7,0 | |||
| 780,9 | 669,3 | 5,7 | 6,9 | |||
| Итого | 1419,3 | 1509,3 | х | х |
Определить:
1) Систему взаимосвязанных индексов
2) Общие (сводные) индексы численности работников, уровня оплаты труда и фонда заработной платы. Построить систему индексов.
3) Абсолютное изменение фонда заработной платы – всего и в том числе за счет численности работников и уровня оплаты их труда.
Решение
1) Строим систему признаков:
Фонд заработной платы(w)=число работников(q) х средняя заработная плата(p)
Таким же образом будут связаны и индексы: Iw = Iq x Ip.
2Система индексов в относительной форме: Iw = Iq x Ip
Таблица 2.9 - Общие индексы в относительной форме
| Индекс фонда заработной платы | 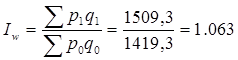
| Фонд заработной платы(ФЗП) в отчетном периоде по сравнению с базисным. вырос на 6,3% |
| Индекс численности работников | 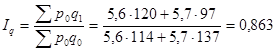
| Под влиянием снижения численности работников ФЗП в отчетном периоде по сравнению с базисным сократился на 13,7% |
| Индекс средней заработной платы | 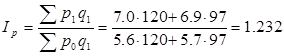
| Под влиянием роста средней зарплаты ФЗП отчетном периоде по сравнению с базисным вырос на 23,2% |
Увязка в систему: индексов: Iw = Iq x Ip., 1,063=0,863 х 1,232
3) Система индексов в абсолютной форме будет иметь вид: Δw = Δw(p) + Δ(q)
Таблица 2.10 - Общие индексы в абсолютной форме
| Абсолютное изменение ФЗП, тыс.руб. | 
| ФЗП вырос в отчетном периоде по сравнению с базисным на 90 тыс.руб. |
| Абсолютное изменение ФЗП под влиянием снижения численности | 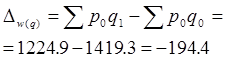
| Снижение численности работников в отчетном периоде по сравнению с базисным привело к сокращению ФЗП работников на 195 тыс.руб. |
| Абсолютное изменение ФЗП под влиянием роста средней зарплаты | 
| Рост ФЗП в отчётном периоде по сравнению с базисным за счет увеличения средней з/пл. составил 284,4 тыс.руб |
Увязка индексов в систему: Δw = Δw(p) + Δ(q)., 90=-194,4+1284,4
2.8. При решении задачи 8 необходимо рассчитать цепные, базисные и средние показатели динамики по следующим формулам:
Таблица 2.11- Цепные и базисные показатели динамики
| Показатели | Цепные | Базисные |
| Абсолютный прирост(Δ) | 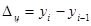
| 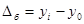
|
| Темп роста (Т), % | 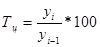
| 
|
| Темп прирост (ТΔ) | 
| 
|
Таблица 2.12 - Средние показатели динамики
| Показатель | Формула |
| Средний уровень: | 
|
| Средний абсолютный прирост | 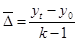
|
| Средний темп роста | 
|
| Средний темп прироста | 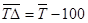
|
Пример решения задачи 5.
Таблица 2.13 - Расчет цепных и базисных показателей динамики
| Год | Уровни ряда yi | Абсолютный прирост цепной Δц =уi-уi-1 | Абсолютный прирост базисный Δб= уi-у0 | Темп роста цепной Тц=(уi / уi-1) *100 | Темп роста базисный Тб=(уi/у0) *100 | Темп прироста цепной Тц-100 | Темп прироста базисный Тб-100 |
| - | - | - | - | - | - | ||
| -3 | -3 | 97,86 | 97,86 | -2,14 | -2,14 | ||
| -1 | -4 | 99,27 | 97,14 | -0,73 | -2,86 | ||
| -7 | -11 | 94,85 | 92,14 | -5,15 | -7,86 | ||
| -9 | -20 | 93,02 | 85,71 | -6,98 | -14,29 | ||
| Итого | х | х | х | х | х | х |
Таблица 2.14 - Средние показатели динамики
| Показатель | Формула |
| Средний уровень: | 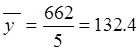 = =
|
| Средний абсолютный прирост | 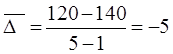
|
| Средний темп роста | 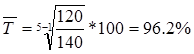
|
| Средний темп прироста | 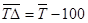 =96,2-100=-3,8% =96,2-100=-3,8%
|
Таблица 2.15 – Аналитическое выравнивание динамического ряда
| Год | Стоимость продукции, млн.руб, yi | 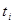
| 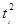
| 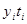
|
| -2 | -280 | |||
| -1 | -137 | |||
| Итого | х | -40 |
Определим параметры уравнения тренда:
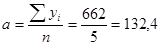
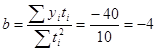
Уравнение тренда: 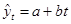 составит
составит 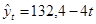
За изучаемый период среднегодовое снижение объема производства составило 4 млн.руб.
ПРИМЕРНЫЙ ПЕРЕЧЕНЬ ВОПРОСОВ ВЫНОСИМЫХ НА ЗАЧЕТ
| 1. | Предмет статистики, ее основные понятия и категории |
| 2. | Методы, применяемые статистикой. |
| 3. | Структура статистической науки. |
| 4. | Виды статистического наблюдения |
| 5. | Формы организации статистического наблюдения |
| 6. | Организация статистики в России |
| 7. | Задачи теории группировок |
| 8. | Виды группировок. (Типологическая группировка, порядок построения) |
| 9. | Виды группировок.(Структурная группировка. Показатели структурных сдвигов). |
| 10. | Статистические таблицы |
| 11. | Абсолютные и относительные величины. Виды относительных величин. |
| 12. | Понятие о средних ве |
|
|
|


