 |
Функция распределения и ее свойства
|
|
|
|
Случайные величины
Определение. Пусть  — произвольное вероятностное пространство.
— произвольное вероятностное пространство.
Случайной величиной 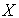 называется измеримая функция
называется измеримая функция  , отображающая
, отображающая  в множество действительных чисел
в множество действительных чисел  , т.е. функция, для которой прообраз
, т.е. функция, для которой прообраз  любого борелевского множества
любого борелевского множества  есть множество из
есть множество из 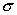 -алгебры
-алгебры 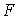 .
.
Примеры случайных величин. 1) Число выпавшее на грани игральной кости.
2) Размер выпускаемой детали. 3) Расстояние от начала координат до случайно брошенной в квадрат точки 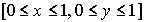 .
.
Множество значений случайной величины 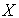 будем обозначать
будем обозначать  , а образ элементарного события
, а образ элементарного события  —
— 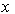 . Множество значений
. Множество значений  может быть конечным, счетным или несчетным.
может быть конечным, счетным или несчетным.
Определим 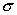 -алгебру на множестве
-алгебру на множестве 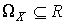 . В общем случае
. В общем случае 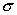 -алгебра числового множества
-алгебра числового множества  может быть образована применением конечного числа операций объединения и пересечения интервалов
может быть образована применением конечного числа операций объединения и пересечения интервалов  или полуинтервалов вида
или полуинтервалов вида 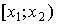 (
( ), в которых одно из чисел
), в которых одно из чисел 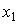 или
или 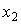 может быть равно
может быть равно 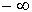 или
или  .
.
В частном случае, когда  — дискретное (не более чем счетное) множество,
— дискретное (не более чем счетное) множество, 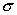 -алгебру образуют любые подмножества множества
-алгебру образуют любые подмножества множества  , в том числе и одноточечные.
, в том числе и одноточечные.
Таким образом 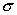 -алгебру множества
-алгебру множества  можно построить из множеств
можно построить из множеств 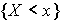 или
или 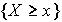 , или
, или  .
.
Будем называть событием  любое подмножество значений
любое подмножество значений  случайной величины
случайной величины 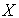 :
: 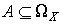 . Прообраз этого события обозначим
. Прообраз этого события обозначим 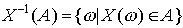 . Ясно, что
. Ясно, что 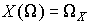 ;
;  ;
; 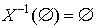 . Все множества
. Все множества  , которые могут быть получены как подмножества
, которые могут быть получены как подмножества  из множества
из множества 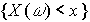 ,
,  , применением конечного числа операций объединения и пересечения, образуют систему событий. Определив множество возможных значений случайной величины
, применением конечного числа операций объединения и пересечения, образуют систему событий. Определив множество возможных значений случайной величины 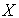 —
—  и выделив систему событий
и выделив систему событий 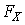 , построим измеримое пространство
, построим измеримое пространство  . Определим вероятность на подмножествах (событиях)
. Определим вероятность на подмножествах (событиях)  из
из  таким образом, чтобы она была равна вероятности наступления события, являющегося его прообразом:
таким образом, чтобы она была равна вероятности наступления события, являющегося его прообразом: 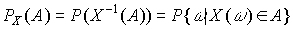 .
.
|
|
|
Тогда тройка 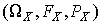 назовем вероятностным пространством случайной величины
назовем вероятностным пространством случайной величины 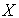 , где
, где 
— множество значений случайной величины 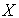 ;
; 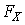 —
— 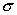 -алгебра числового множества
-алгебра числового множества  ;
; 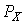 — функция вероятности случайной величины
— функция вероятности случайной величины 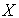 .
.
Если каждому событию 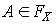 поставлено в соответствие
поставлено в соответствие  , то говорят, что задано распределение случайной величины
, то говорят, что задано распределение случайной величины 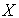 . Функция
. Функция  задается на таких событиях (базовых), зная вероятности которых можно вычислить вероятность произвольного события
задается на таких событиях (базовых), зная вероятности которых можно вычислить вероятность произвольного события  . Тогда событиями могут быть события
. Тогда событиями могут быть события 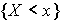 .
.
Функция распределения и ее свойства
Рассмотрим вероятностное пространство 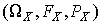 , образованное случайной величиной
, образованное случайной величиной 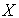 .
.
Определение. Функцией распределения случайной величины 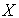 называется функция
называется функция  действительного переменного
действительного переменного 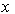 , определяющая вероятность того, что случайная величина
, определяющая вероятность того, что случайная величина 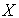 примет в результате реализации эксперимента значение, меньшее некоторого фиксированного числа
примет в результате реализации эксперимента значение, меньшее некоторого фиксированного числа 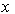 :
:
 (1)
(1)
Там где понятно, о какой случайной величине 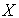 ,
, 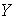 или
или 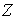 идет речь, вместо
идет речь, вместо  будем писать
будем писать 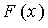 . Если рассматривать случайную величину
. Если рассматривать случайную величину 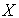 как случайную точку на оси
как случайную точку на оси  , то функция распределения
, то функция распределения 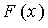 с геометрической точки зрения это вероятность того, что случайная точка
с геометрической точки зрения это вероятность того, что случайная точка 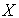 в результате реализации эксперимента попадет левее точки
в результате реализации эксперимента попадет левее точки 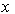 .
.
Очевидно что функция  при любом
при любом 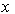 удовлетворяет неравенству
удовлетворяет неравенству 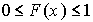 . Функция распределения случайной величины
. Функция распределения случайной величины 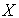 имеет следующие свойства:
имеет следующие свойства:
2) Функция распределения — неубывающая функция 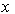 , т.е. для любых
, т.е. для любых 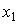 и
и 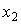 , таких что
, таких что  , имеет место неравенство
, имеет место неравенство  .
.
Доказательство. Пусть 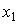 и
и 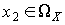 и
и  . Событие, состоящее в том, что
. Событие, состоящее в том, что 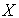 примет значение, меньшее, чем
примет значение, меньшее, чем 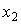 ,
, 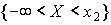 представим в виде объединения двух несовместных событий
представим в виде объединения двух несовместных событий  и
и 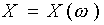 :
:  .
.
Тогда согласно аксиоме 3 Колмогорова, 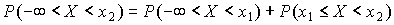 или по формуле (1)
или по формуле (1)
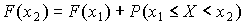 , (2)
, (2)
откуда  , так как
, так как  . Свойство доказано.
. Свойство доказано.
Теорема. Для любых 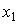 и
и 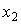 вероятность неравенства
вероятность неравенства 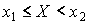 вычисляется по формуле
вычисляется по формуле
 (3)
(3)
Доказательство. Справедливость формулы (3) следует из соотношения (2). Таким образом, вероятность попадания случайной величины 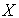 в полуинтервал
в полуинтервал 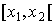 равна разности значений функции распределения вычисленных на концах полуинтервала
равна разности значений функции распределения вычисленных на концах полуинтервала 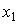 и
и 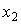 .
.
|
|
|
2)  ;
; 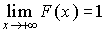 .
.
Доказательство. Пусть 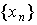 и
и 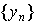 — две монотонные числовые последовательности, причем
— две монотонные числовые последовательности, причем  ,
, 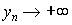 при
при  . Событие
. Событие  состоит в том, что
состоит в том, что  . Достоверное событие
. Достоверное событие 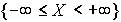 эквивалентно объединению событий
эквивалентно объединению событий  :
:
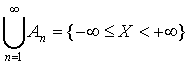 ;
; 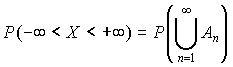 .
.
Так как 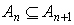 , то по свойству вероятностей
, то по свойству вероятностей 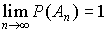 , т.е.
, т.е. 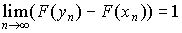 .
.
Принимая во внимание определение предела, получаем 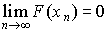 ;
; 
3) Функция  непрерывна слева в любой точке
непрерывна слева в любой точке 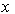 ,
, 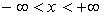
Доказательство. Пусть 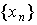 — любая возрастающая последовательность чисел, сходящаяся к
— любая возрастающая последовательность чисел, сходящаяся к 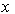 . Тогда можно записать:
. Тогда можно записать: 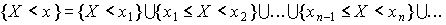
На основании аксиомы 3 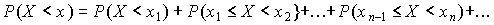
Так как ряд справа состоит из положительных чисел и сходится к 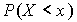 , то остаток ряда, начиная с некоторого номера
, то остаток ряда, начиная с некоторого номера 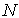 , будет меньше
, будет меньше  ,
, 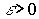 (теорема об остатке ряда)
(теорема об остатке ряда)
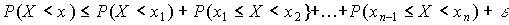 .
.
Используя формулу (3), выразим вероятности событий через функцию распределения. Получим
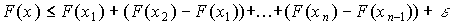 ,
,
откуда  или
или 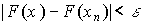 , а это означает, что
, а это означает, что 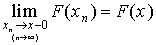 .
.
Из рассмотренных свойств следует, что каждая функция распределения  является 1) неубывающей, 2) непрерывной слева и 3) удовлетворяет условию
является 1) неубывающей, 2) непрерывной слева и 3) удовлетворяет условию  и
и 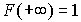 . И, обратно, каждая функция, обладающая свойствами 1), 2), 3), может рассматриваться как функция распределения некоторой случайной величины.
. И, обратно, каждая функция, обладающая свойствами 1), 2), 3), может рассматриваться как функция распределения некоторой случайной величины.
Теорема. Вероятность того, что значение случайной величины больше действительного числа 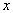 , вычисляется по формуле
, вычисляется по формуле 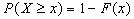 .
.
Доказательство. Достоверное событие 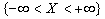 представим в виде объединения двух несовместных событий
представим в виде объединения двух несовместных событий 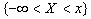 и
и  . Тогда по 3-1 аксиоме Колмогорова
. Тогда по 3-1 аксиоме Колмогорова  или
или 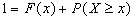 , откуда следует искомая формула.
, откуда следует искомая формула.
Определение. Будем говорить, что функция распределения 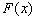 имеет при
имеет при 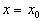 скачок
скачок  , если
, если 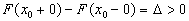 , где
, где 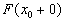 и
и 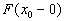 пределы слева и справа функции распределения
пределы слева и справа функции распределения 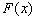 в точке
в точке 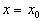 .
.
Теорема. Для каждого 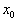 из пространства
из пространства 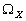 случайной величины
случайной величины 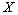 имеет место формула
имеет место формула 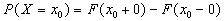
Доказательство. Приняв в формуле (3)  ,
,  и перейдя к пределу при
и перейдя к пределу при  ,
, 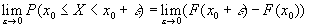 , согласно свойству 3), получим искомый результат.
, согласно свойству 3), получим искомый результат.
Можно показать, что функция 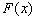 может иметь не более чем счетное число скачков. Действительно функция распределения может иметь не более одного скачка
может иметь не более чем счетное число скачков. Действительно функция распределения может иметь не более одного скачка  , скачков
, скачков  — не более 3-х, скачков
— не более 3-х, скачков 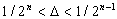 не более чем
не более чем 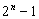 .
.
Иногда поведение случайной величины 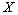 характеризуется не заданием ее функции распределения, а каким-либо другим законом распределения, но так, чтобы можно было получить из этого закона распределения функцию распределения
характеризуется не заданием ее функции распределения, а каким-либо другим законом распределения, но так, чтобы можно было получить из этого закона распределения функцию распределения 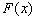 .
.
|
|
|
|
|
|


