Методика определения коэффициентов критериального

Уравнения c использованием средств MATLAB

 

Для решения задачи обобщенной нелинейной регрессии в MATLAB имеется функция lsqnonlin(), возвращающая решение задачи нахождения точки минимума функции f(x)

(3.8)

 

где в общем случае f(x) – вектор-функция, х – вектор-столбец искомых переменных, L – некоторая константа.

Синтаксис функции lsqnonlin():

 

x = lsqnonlin(fun, x0)

x = lsqnonlin(fun, x0, lb, ub)

x = lsqnonlin(fun, x0, lb, ub, options)

x = lsqnonlin(fun, x0, lb, ub, options, P1, P2, …),

 

здесь fun – название минимизируемой функции;

х0 – начальная точка, с которой начинается процесс поиска минимума функции;

lb, ub – соответственно левая и правая границы отрезка, на котором определяется минимум функции;

options – параметр, задающий режим работы функции оптимизирующей функции (перечень возможных значений данного параметра приведен в Help MATLAB в главе Optimization Toolbox в разделе Optimization Parameters);

P1, P2, … – параметры, от которых зависит функция fun.

 

Рассмотрим пример, демонстрирующий использование данной функции для нахождения коэффициентов функции 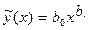при следующих значениях экспериментальных данных:

x (Re)
y (Nu)	10.16	24.42	29.56	33.15	34.57	21.2	19.81	2.21

 

М-файл:

function z=LR7_5(Coeff,vx,vy);

k=1:length(vx);

z=vy-(Coeff(1)*vx.^Coeff(2));

Текст программы:

function z= LR7_5 (Coeff,vx,vy);

x=[1000:2000:15000];

y=[10.16 24.42 29.56 33.15 34.57 21.2 19.81 2.21];

xi=[1000:10:15000];

z=[1 2];

Coeff = lsqnonlin(‘LR7_5’,z,[],[],[],x,y);

F=inline('b0*x.^b1','x','b0','b1')

yi=feval(F,xi,Coeff(1),Coeff(2));

plot(x, y, 'ko',xi, yi, 'k');

title('Аппрокcимация данных при помощи регреccии b0*x.^b1');

xlabel('\itx');

ylabel('\ity').

 

Coeff = 17.256 0.027224

Проверка адекватности полученных уравнений

 

Для оценки качества полученных критериальных уравнений необходимо использовать: 1) корреляционное отношение и 2) критерий Фишера.

Корреляционное отношение q используется для оценки силы (тесноты) нелинейной связи (проведения корреляционного анализа):

 

, (3.9)

 

где f₁=N – 1, f₂=N – l – числа степеней свободы; l – число связей, наложенных на выборку (для уравнения регрессии это число определяемых коэффициентов 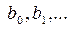); – остаточная дисперсия; 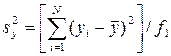– дисперсия относительно среднего.

Чем больше q, тем сильнее связь (0£q£1). При q=0 однозначное отсутствие связи между случайными величинами возможно только для нормального распределения. В случае линейной регрессии (l=2) корреляционное отношение равно коэффициенту корреляции q=|r^* |.

Критерий Фишера F используется для оценки качества аппроксимации (проведение регрессионного анализа). При отсутствии параллельных опытов и, следовательно, дисперсии воспроизводимости, а также нормальном распределении случайных величин y_i качество аппроксимации можно оценить по [1]. В данном случае он показывает, во сколько раз уменьшается рассеяние относительно полученного уравнения регрессии по сравнению с рассеянием относительно среднего. Чем больше значение F превышает табличное (или f – распределение в табл. 3.1) для выбранного уровня вероятности (значимости, надежности) p (обычно p =0.95) и чисел 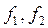, тем эффективнее уравнение регрессии.

Таблица 3.1

	Степень свободы
									--
	161,4	199,5	215.7	224,6	230,2	234,0	238,9	243,9	249,0	254,3
	18,51	19,00	19,16	19,25	19,30	19,33	19,37	19,41	19,46	19,50
	10,13	9,55	9,28	9,12	9,01	8,94	8,84	8,74	8,64	8,53
	7,71	6,94	6,59	6,39	6,26	6,16	6,04	5,91	5,77	5,63
	6,61	5,79	5,41	5,19	5,05	4,95	4,82	4,68	4,53	4,36
	5,99	5,14	4,76	4,53	4,39	4,28	4,15	4,00	3,84	3,67
	5,59	4,74	4,35	4,12	3,97	3,87	3,73	3,57	3,41	3,23

Окончание табл. 3.1

	5,32	4,46	4,07	3,84	3,69	3,58	3,44	3,28	3,12	2,93
	5,12	4,26	3,86	3,63	3,48	3,37	3,23	3,07	2,90	2,71
	4,96	4,10	3,71	3,48	3,33	3,22	3,07	2,91	2,74	2,540
	4,84	3,98	3,59	3,36	3,20	3,09	2,95	2,79	2,61	2,40
	4,75	3,88	3,49	3,26	3,11	3,00	2,85	2,69	2,50	2,30
	4,67	3,80	3,41	3,18	3,02	2,92	2,77	2,60	2,42	2,21
	4,60	3,74	3,34	3,11	2,96	2,85	2,70	2,53	2,35	2,13
	4,54	3,68	3,29	3,06	2,90	2,79	2,64	2,48	2,29	2,07

 

Порядок выполнения работы

 

1. Для различных значений расходов сжатого воздуха, при которых исследовалась экспериментальная теплопередающая поверхность в лаб. раб № 2 определить значения скоростей и по (2.2) значение критерия Рейнольдса, характеризующего режим течения среды. Значения данного критерия использовать как значения аргумента x искомой регрессии .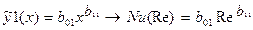

2. Полученные по результатам исследований экспериментальные значения критерия Нуссельта использовать как значения искомой функции.

3. Определить при помощи средств MATLAB коэффициенты .

4. Полученные по результатам исследований экспериментальные значения коэффициента сопротивления по длине использовать как значения искомой функции .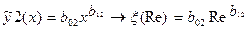

5. Определить при помощи средств MATLAB коэффициенты .

 

Содержание отчета

 

1. Указать название и цель работы.

2. Привести чертежи исследуемых теплопередающих поверхностей.

3. Привести экспериментальные значения критериев Рейнольдса, Нуссельта, коэффициентов сопротивления по длине для исследуемой теплопередающей поверхности при различных расходах (скоростях) сжатого воздуха.

4. Привести текст программы MATLAB и вид полученных уравнений.

5. Оценить адекватность полученных критериальных уравнений.

 

Список рекомендуемой литературы

 

1. Январев, И.А. Математические методы моделирования физических процессов: метод. указания / Сост. И.А. Январев. Омск: Изд-во ОмГТУ, 2006. 80 с.

Практическая работа № 1

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: