 |
Проверка гипотезы о значении математического ожидания при неизвестной дисперсии генеральной совокупности
|
|
|
|
Когда выборка извлечена из нормально распределенной генеральной совокупности с неизвестными параметрами  и
и  , причем объем выборки
, причем объем выборки 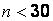 , для проверки нулевой гипотезы о том, что математическое ожидание генеральной совокупности равно
, для проверки нулевой гипотезы о том, что математическое ожидание генеральной совокупности равно 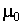 (
( ) используют статистику
) используют статистику
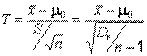 , где
, где 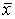 – выборочное среднее,
– выборочное среднее, 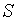 – несмещенная оценка СКО генеральной совокупности,
– несмещенная оценка СКО генеральной совокупности, 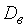 – выборочная дисперсия. Если нулевая гипотеза верна, случайная величина
– выборочная дисперсия. Если нулевая гипотеза верна, случайная величина 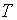 распределена по закону Стьюдента с числом степеней свободы
распределена по закону Стьюдента с числом степеней свободы 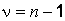 (разд. 3).
(разд. 3).
Альтернативная гипотеза, область принятия гипотезы и критическая область выбираются в соответствии с условиями задачи. Возможны три варианта формулировки альтернативной гипотезы:
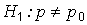 , критическая область – двусторонняя;
, критическая область – двусторонняя;
 , критическая область – левосторонняя;
, критическая область – левосторонняя;
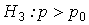 , критическая область – правосторонняя.
, критическая область – правосторонняя.
Пример 4.3. По паспортным данным автомобильного двигателя, расход топлива на 100 км пробега составляет 10 л. В результате изменения конструкции двигателя ожидается, что расход топлива уменьшится. Для проверки были испытаны 25 случайно отобранных автомобилей с модернизированным двигателем. Средний расход топлива на 100 км пробега оказался равным 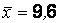 л. Несмещенная оценка СКО расхода топлива равно 2 л. Можно ли утверждать, что изменение конструкции двигателя не повлияло на расход топлива? Положить
л. Несмещенная оценка СКО расхода топлива равно 2 л. Можно ли утверждать, что изменение конструкции двигателя не повлияло на расход топлива? Положить 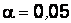 . Считать, что выборка произведена из нормальной генеральной совокупности.
. Считать, что выборка произведена из нормальной генеральной совокупности.
Решение. По условию задачи требуется проверить нулевую гипотезу 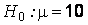 л против альтернативной
л против альтернативной 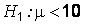 л (модернизированный двигатель расходует меньше топлива). Если нулевая гипотеза верна, то случайная величина
л (модернизированный двигатель расходует меньше топлива). Если нулевая гипотеза верна, то случайная величина
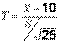
имеет распределение Стьюдента с числом степеней свободы  . По таблице распределения Стьюдента (прил. 4), учитывая
. По таблице распределения Стьюдента (прил. 4), учитывая 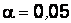 и
и 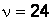 , находим критическое значение в случае левосторонней гипотезы
, находим критическое значение в случае левосторонней гипотезы 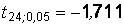 (распределение Стьюдента симметрично относительно нуля). Вычислим экспериментальное значение статистики:
(распределение Стьюдента симметрично относительно нуля). Вычислим экспериментальное значение статистики:
|
|
|
 .
.
Поскольку экспериментальное значение критерия больше критического, оно попадает в областьпринятия нулевой гипотезы, поэтому 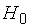 не отвергается, т. е. нет оснований считать, что новая конструкция двигателя позволила уменьшить расход топлива.
не отвергается, т. е. нет оснований считать, что новая конструкция двигателя позволила уменьшить расход топлива.
№ 63 Проверка гипотезы о дисперсии.
Проверка гипотезы о числовом значении дисперсии нормально распределённой случайной величины Пусть — нормально распределенная случайная величина с неизвестной дисперсией D = 2, представленная выборочными значениями
x1, x2, …, xn. Задача состоит в проверке гипотезы о том, что неизвестный параметр 2 равен заданному числу. Пусть дана некоторая оценка 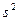 неизвестной дисперсии
неизвестной дисперсии  , построенная по выборке
, построенная по выборке
x1, x2, …, xn.
Предположим, что истинное значение дисперсии равно 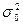 . Поскольку оценка
. Поскольку оценка 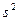 — случайная величина, то выборочное значение
— случайная величина, то выборочное значение 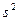 , вряд ли будет совпадать с
, вряд ли будет совпадать с 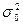 . В связи с этим возникает вопрос: при каком отклонении
. В связи с этим возникает вопрос: при каком отклонении 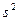 от
от 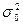 и с какой степенью уверенности можно утверждать, что истинное значение дисперсии
и с какой степенью уверенности можно утверждать, что истинное значение дисперсии  отлично от
отлично от 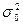 ? Ответом на этот вопрос может быть значение вероятности того, что величина
? Ответом на этот вопрос может быть значение вероятности того, что величина 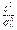 , вычисленная в предположении, что
, вычисленная в предположении, что 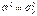 , больше некоторого фиксированного числа.
, больше некоторого фиксированного числа.
Если эта вероятность мала, то мы являемся свидетелями маловероятного события, т.е. отличие эмпирического значения 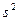 от гипотетического значения
от гипотетического значения 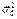 представляется значимым и гипотеза о том, что
представляется значимым и гипотеза о том, что  должна быть отвергнута. Если же эта вероятность велика, то отклонение
должна быть отвергнута. Если же эта вероятность велика, то отклонение 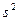 от
от 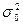 , по-видимому, обусловлено естественной случайностью, и гипотеза
, по-видимому, обусловлено естественной случайностью, и гипотеза  может быть принята. Сформулируем нулевую гипотезу о том, что дисперсия нормального распределения 2 равна заранее заданному числу 02 — H0:2 = 02. В процедуре проверки гипотезы будет использован критерий
может быть принята. Сформулируем нулевую гипотезу о том, что дисперсия нормального распределения 2 равна заранее заданному числу 02 — H0:2 = 02. В процедуре проверки гипотезы будет использован критерий
|
|
|
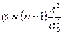 , где
, где  и
и  — несмещенные точечные оценки дисперсии и математического ожидания. Критерий ϕ имеет распределение 2 с (n-1) степенями свободы. Рассмотрим три случая альтернативных гипотез:
— несмещенные точечные оценки дисперсии и математического ожидания. Критерий ϕ имеет распределение 2 с (n-1) степенями свободы. Рассмотрим три случая альтернативных гипотез:
H1: 2 ≠ 02;
H1: 2 > 02; H1: 2 < 02.
В первом из этих случаев, двусторонняя альтернатива H1:2 ≠ 02, критическая область двусторонняя и ее границы определяются из условий  и
и 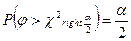 .
.
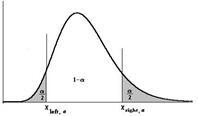
Критическая область для альтернативной гипотезы H1:2≠02 Зададимся некоторым уровнем значимости и найдем значение 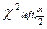 и
и 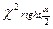 уравнения как решения уравнений
уравнения как решения уравнений
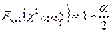
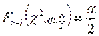 где
где 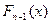 — функция распределения 2 с (n –1) степенями свободы. Когда критическая область найдена, можно по выборке вычислить значение критерия ϕ и проверить попадает ли это значение в критическую область или в область принятия гипотезы.
— функция распределения 2 с (n –1) степенями свободы. Когда критическая область найдена, можно по выборке вычислить значение критерия ϕ и проверить попадает ли это значение в критическую область или в область принятия гипотезы.
№ 64 Проверка гипотезы о равенстве математического ожидания при известной дисперсии.
Проверка гипотезы о равенстве математических ожиданий двух генеральных совокупностей Пусть из каждой из двух нормально распределенных генеральных совокупностей 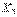 (с параметрами
(с параметрами 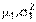 ) и
) и  (с параметрами
(с параметрами 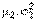 ) извлечены выборки объема
) извлечены выборки объема 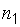 и
и 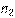 соответственно. Требуется проверить нулевую гипотезу
соответственно. Требуется проверить нулевую гипотезу 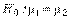 о равенстве средних значений этих генеральных совокупностей. Альтернативная гипотеза формулируется в соответствии с условиями задачи или эксперимента:
о равенстве средних значений этих генеральных совокупностей. Альтернативная гипотеза формулируется в соответствии с условиями задачи или эксперимента:
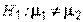 (двустороння критическая область);
(двустороння критическая область);
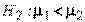 (левостороння критическая область);
(левостороння критическая область);
 (правостороння критическая область).
(правостороння критическая область).
Случай, когда дисперсии генеральных совокупностей  и
и 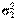 известны. В этом случае для проверки нулевой гипотезы используют случайную величину
известны. В этом случае для проверки нулевой гипотезы используют случайную величину
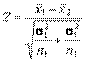 , где
, где 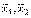 – выборочные средние первой и второй выборок соответственно. Если нулевая гипотеза справедлива, то статистика
– выборочные средние первой и второй выборок соответственно. Если нулевая гипотеза справедлива, то статистика 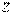 имеет нормальное распределение с математическим ожиданием, равным нулю и дисперсией, равной единице (разд. 3). Критическое значение выбирается в соответствии с задаваемым уровнем значимости по таблице значений функции Лапласа (прил. 2) или стандартного нормального распределения.
имеет нормальное распределение с математическим ожиданием, равным нулю и дисперсией, равной единице (разд. 3). Критическое значение выбирается в соответствии с задаваемым уровнем значимости по таблице значений функции Лапласа (прил. 2) или стандартного нормального распределения.
Если объемы выборок достаточно велики 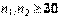 , то случайную величину
, то случайную величину 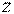 можно использовать и при неизвестных дисперсиях генеральных совокупностей, положив в выражении для
можно использовать и при неизвестных дисперсиях генеральных совокупностей, положив в выражении для 
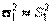 ,
, 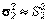 .
.
|
|
|
Эту же статистику используют и при проверке гипотезы о равенстве вероятностей «успеха». Объемы выборок  должны быть достаточно велики, чтобы биномиальное распределение можно было бы приближенно считать нормальным.
должны быть достаточно велики, чтобы биномиальное распределение можно было бы приближенно считать нормальным.
Пример 4.7. Двое рабочих на одинаковых станках изготовляют одинаковые детали. Есть ли значимая разница между долями выпускаемого ими брака? Была собрана следующая информация: 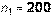 ,
,  ,
, 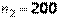 ,
, 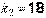 (число деталей, изготовленных первым и вторым рабочими соответственно и число бракованных деталей у первого и второго рабочих). Положить
(число деталей, изготовленных первым и вторым рабочими соответственно и число бракованных деталей у первого и второго рабочих). Положить 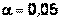 .
.
Решение. Согласно условиям задачи требуется проверить нулевую гипотезу о равенстве значений вероятности 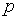 «успеха» – появления бракованной детали (
«успеха» – появления бракованной детали (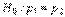 ) для первого и второго рабочего, причем, поскольку объем выборки достаточно велик, можно использовать статистику
) для первого и второго рабочего, причем, поскольку объем выборки достаточно велик, можно использовать статистику 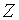 . Поскольку
. Поскольку 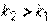 , то альтернативную гипотезу следует принять в виде
, то альтернативную гипотезу следует принять в виде 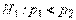 (левосторонняя критическая область).Итак, было обследовано
(левосторонняя критическая область).Итак, было обследовано 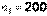 деталей, изготовленных первым рабочим, из них
деталей, изготовленных первым рабочим, из них  – оказались бракованными, тогда
– оказались бракованными, тогда 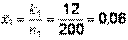 ,
, 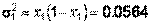 .
.
Аналогично для второго рабочего 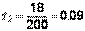 ,
, 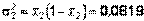 . Тогда экспериментальное значение статистики:
. Тогда экспериментальное значение статистики:  .Для
.Для  критическое значение равно
критическое значение равно  , таким образом,
, таким образом, 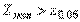 . Следовательно, нулевая гипотеза отвергается: нельзя утверждать, что второй рабочий в среднем делает больше брака, чем первый.
. Следовательно, нулевая гипотеза отвергается: нельзя утверждать, что второй рабочий в среднем делает больше брака, чем первый.
Случай, когда дисперсии генеральных совокупностей  и
и 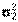 неизвестны, но известно, что
неизвестны, но известно, что  . Для проверки нулевой гипотезы используется случайная величина
. Для проверки нулевой гипотезы используется случайная величина
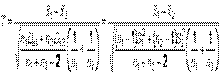 ,
,
№ 65 Проверка гипотезы о равенстве математического ожидания при неизвестной дисперсии.
Проверка гипотезы о равенстве математических ожиданий двух нормально распределенных случайных величин (малы Рассмотрим ту же задачу, что и в предыдущем пункте 3.4, но только при условии, что объемы выборок 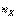 и
и 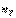 Невелики (меньше 30). В этом случае замена генеральных дисперсий
Невелики (меньше 30). В этом случае замена генеральных дисперсий 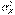 и
и 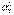 , входящих в (3.15), на исправленные выборочные дисперсии
, входящих в (3.15), на исправленные выборочные дисперсии 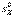 и
и 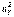 может привести к большой ошибке в величине
может привести к большой ошибке в величине  , а следовательно, к большой ошибке в установлении области
, а следовательно, к большой ошибке в установлении области  принятия гипотезы Н0. Однако если есть уверенность в том, что неизвестные генеральные
принятия гипотезы Н0. Однако если есть уверенность в том, что неизвестные генеральные 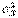 и
и 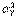 Одинаковы (например, если сравниваются средние размеры двух партий деталей, изготовленных на одном и том же станке), то можно, используя распределение Стьюдента, и в этом случае построить критерий проверки гипотезы Н0 о равенстве математических ожиданий величин X и Y. Для этого вводят случайную величину
Одинаковы (например, если сравниваются средние размеры двух партий деталей, изготовленных на одном и том же станке), то можно, используя распределение Стьюдента, и в этом случае построить критерий проверки гипотезы Н0 о равенстве математических ожиданий величин X и Y. Для этого вводят случайную величину 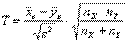 )Где
)Где
|
|
|
 - среднее из исправленных выборочных дисперсий
- среднее из исправленных выборочных дисперсий 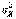 и
и 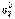 , служащее точечной оценкой обеих одинаковых неизвестных генеральных дисперсий
, служащее точечной оценкой обеих одинаковых неизвестных генеральных дисперсий 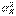 и
и 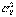 . Как оказывается (см. [3], стр.180), при справедливости нулевой гипотезы Н0 случайная величина Т имеет распределение Стьюдента с
. Как оказывается (см. [3], стр.180), при справедливости нулевой гипотезы Н0 случайная величина Т имеет распределение Стьюдента с 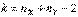 степенями свободы независимо от величин
степенями свободы независимо от величин 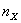 и
и 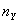 объемов выборок. Если гипотеза Н0 верна, то разница
объемов выборок. Если гипотеза Н0 верна, то разница  должна быть невелика. То есть экспериментальное значение TЭксп. величины Т должно быть невелико. А именно, должно заключаться в некоторых границах
должна быть невелика. То есть экспериментальное значение TЭксп. величины Т должно быть невелико. А именно, должно заключаться в некоторых границах 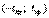 . Выход же его за эти границы мы будем считать опровержением гипотезы Н0, и допускать это будем с вероятностью, равной задаваемому уровню значимости α. Таким образом, областью принятия гипотезы Н0 будет являться некоторый интервал
. Выход же его за эти границы мы будем считать опровержением гипотезы Н0, и допускать это будем с вероятностью, равной задаваемому уровню значимости α. Таким образом, областью принятия гипотезы Н0 будет являться некоторый интервал 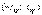 , в который значения случайной величины Т должны попадать с вероятностью 1- α:
, в который значения случайной величины Т должны попадать с вероятностью 1- α:
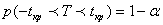 (3.18)
(3.18)
Величину 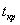 , определяемую равенством (3.18), для различных уровней значимости α и различных числах Kстепеней свободы величины Т можно найти в таблице критических точек распределения Стьюдента (таблице 4 Приложения). Тем самым будет найден интервал
, определяемую равенством (3.18), для различных уровней значимости α и различных числах Kстепеней свободы величины Т можно найти в таблице критических точек распределения Стьюдента (таблице 4 Приложения). Тем самым будет найден интервал  принятия гипотезы Н0. И если экспериментальное значение TЭксп величины Т попадет в этот интервал – гипотезу Н0 принимают. Не попадает - не принимают.
принятия гипотезы Н0. И если экспериментальное значение TЭксп величины Т попадет в этот интервал – гипотезу Н0 принимают. Не попадает - не принимают.
Примечание 1. Если нет оснований считать равными генеральные дисперсии 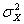 и
и 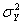 величин Х и Y, то и в этом случае для проверки гипотезы Н0 о равенстве математических ожиданий величин Х и Y допускается использование изложенного выше критерия Стьюдента. Только теперь у величины Т число K степеней свободы следует считать равным не
величин Х и Y, то и в этом случае для проверки гипотезы Н0 о равенстве математических ожиданий величин Х и Y допускается использование изложенного выше критерия Стьюдента. Только теперь у величины Т число K степеней свободы следует считать равным не 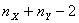 , а равным (см. [1])
, а равным (см. [1])
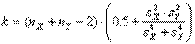 (3.19)
(3.19)
Если исправленные выборочные дисперсии  и
и  различаются существенно, то второе слагаемое в последней скобке (3.19) невелико по сравнению с 0,5, так что выражение (3.19) по сравнению с выражением
различаются существенно, то второе слагаемое в последней скобке (3.19) невелико по сравнению с 0,5, так что выражение (3.19) по сравнению с выражением 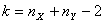 уменьшает число степеней свободы случайной величины Т почти вдвое. А это ведет к существенному расширению интервала
уменьшает число степеней свободы случайной величины Т почти вдвое. А это ведет к существенному расширению интервала 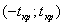 принятия гипотезы Н0 и, соответственно, к существенному сужению критической области непринятия этой гипотезы. И это вполне справедливо, так как степень разброса возможных значений разности
принятия гипотезы Н0 и, соответственно, к существенному сужению критической области непринятия этой гипотезы. И это вполне справедливо, так как степень разброса возможных значений разности 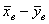 Будет, в основном, определяться разбросом значений той из величин Х и Y, которая имеет большую дисперсию. То есть информация от выборки с меньшей дисперсией как бы пропадает, что и ведет к большей неопределенности в выводах о гипотезе Н0.
Будет, в основном, определяться разбросом значений той из величин Х и Y, которая имеет большую дисперсию. То есть информация от выборки с меньшей дисперсией как бы пропадает, что и ведет к большей неопределенности в выводах о гипотезе Н0.
|
|
|
№ 66 Совпадение дисперсий двух нормальных выборок
Есть две независимые выборки из нормальных распределений: 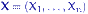 из
из 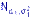 и
и 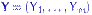 из
из 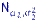 , средние которых, вообще говоря, неизвестны. Критерий Фишера предназначен для проверки гипотезы
, средние которых, вообще говоря, неизвестны. Критерий Фишера предназначен для проверки гипотезы 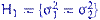 .Обозначим через
.Обозначим через 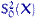 и
и 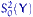 несмещенные выборочные дисперсии:
несмещенные выборочные дисперсии: 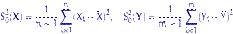 и зададим функцию отклонения
и зададим функцию отклонения  как их отношение
как их отношение 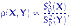 Теорема 11. Если гипотеза
Теорема 11. Если гипотеза  верна, то случайная величина
верна, то случайная величина 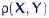 имеет распределение Фишера
имеет распределение Фишера 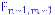 с
с 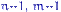 степенями свободы. Доказательство. По лемме Фишера, независимые случайные величины
степенями свободы. Доказательство. По лемме Фишера, независимые случайные величины
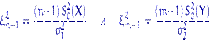
имеют распределения  и
и 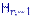 соответственно. При
соответственно. При  отношение
отношение
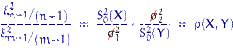
имеет распределение Фишера с 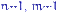 степенями свободы по определению 18 и совпадает с
степенями свободы по определению 18 и совпадает с 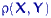 .С условием K1(б) дело обстоит сложнее.
.С условием K1(б) дело обстоит сложнее.
Упражнение. Доказать, что для любой альтернативы 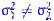
 Построим критерий Фишера и убедимся, что (27) обеспечивает его состоятельность. Возьмем квантили
Построим критерий Фишера и убедимся, что (27) обеспечивает его состоятельность. Возьмем квантили 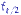 и
и 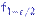 распределения Фишера
распределения Фишера  . Критерием Фишера называют критерий
. Критерием Фишера называют критерий
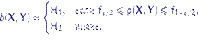
Доказательство состоятельности критерия Фишера. Покажем, что последовательность квантилей  любого уровня
любого уровня 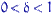 распределения
распределения  сходится к 1 при
сходится к 1 при 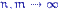 . Возьмем величину
. Возьмем величину  с этим распределением. По определению,
с этим распределением. По определению,  ,
, 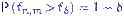 при всех
при всех 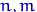 . По свойству 2 распределения Фишера,
. По свойству 2 распределения Фишера, 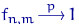 . Поэтому для любого
. Поэтому для любого 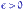 обе вероятности
обе вероятности 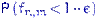 и
и 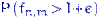 стремятся к нулю при
стремятся к нулю при 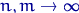 , становясь рано или поздно меньше как
, становясь рано или поздно меньше как 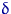 , так и
, так и  . Следовательно, при достаточно больших
. Следовательно, при достаточно больших 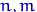 выполнено
выполнено 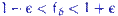 . Для доказательства состоятельности осталось предположить, что гипотеза
. Для доказательства состоятельности осталось предположить, что гипотеза  не верна, взять
не верна, взять  равное, например, половине расстояния от 1 до
равное, например, половине расстояния от 1 до 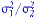 и использовать сходимость (27). Пусть, скажем, при достаточно больших
и использовать сходимость (27). Пусть, скажем, при достаточно больших 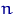 и
и 
 Тогда вероятность ошибки второго рода удовлетворяет неравенствам
Тогда вероятность ошибки второго рода удовлетворяет неравенствам

 Аналогично рассматривается случай, когда (при достаточно больших
Аналогично рассматривается случай, когда (при достаточно больших 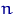 и
и  )
)
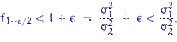
№ 67 Проверка гипотезы о нормальном распределении генеральной совокупности Проверка гипотезы о предполагаемом законе неизвестного распределения производится так же, как и проверка гипотезы о параметрах распределения, т. е. при помощи специально подобранной случайной величины – критерия согласия.Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения.Имеется несколько критериев согласия: Пирсона К., Колмагорова, Смирнова и др.Ограничимся описанием применения критерия Пирсона и проверки гипотезы о нормальном распределении генеральной совокупности. С этой же целью будем сравнивать эмпирические (наблюдаемые) и теоретические частоты (вычисленные в предположении нормального распределения).Обычно эмпирические и теоретические частоты различаются. Случайно ли расхождение частот? Возможно, что расхождение случайно и объясняется малым числом наблюдений либо способом их группировки, либо другими причинами. Возможно, что расхождение частот неслучайно (значимо) и объясняется тем, что теоретические частоты вычислены исходя из неверной гипотезы о нормальном распределении генеральной совокупности.Критерий Пирсона отвечает на поставленный выше вопрос. Правда, как и любой критерий, он не доказывает справедливость гипотезы, а лишь устанавливает на принятом уровне значимости ее согласие или несогласие с данным наблюдением.Пусть по выборке объема n получено эмпирическое распределение: варианты xi – x1 x2 xs,эмпирические частоты ni – n1 n2 ns.Допустим, что в предположении нормального распределения генеральной совокупности вычислены теоретические частоты ni’. При условии значимости a требуется проверить нулевую гипотезу о нормальном распределении генеральной совокупности.В качестве критерия проверки нулевой гипотезы 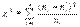 примем случайную величину, где ni –эмпирические частоты, ni’- теоретические частоты.Эта величина случайная, так как в различных опытах она принимает различные, заранее неизвестные значения. Ясно, что чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия и, следовательно, он в известной степени характеризует близость эмпирического и теоретического распределения.Число степеней свободы находят по равенству k=s-1-r,где s – число групп (частичных интервалов) выборки; r – число параметров предполагаемого распределения, которые оценены по данным выборки.В частности, если предполагаемое распределение нормальное, то оценивают два параметра (математическое ожидание и среднее квадратичное отклонение). Поэтому r = 2 и число степеней свободы
примем случайную величину, где ni –эмпирические частоты, ni’- теоретические частоты.Эта величина случайная, так как в различных опытах она принимает различные, заранее неизвестные значения. Ясно, что чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия и, следовательно, он в известной степени характеризует близость эмпирического и теоретического распределения.Число степеней свободы находят по равенству k=s-1-r,где s – число групп (частичных интервалов) выборки; r – число параметров предполагаемого распределения, которые оценены по данным выборки.В частности, если предполагаемое распределение нормальное, то оценивают два параметра (математическое ожидание и среднее квадратичное отклонение). Поэтому r = 2 и число степеней свободы
k=s-1-r =s-1-2=s-3.
Если, например, предполагают, что генеральная совокупность распределена по закону Пуассона, то оценивают один параметр. Поэтому r = 1 и k=s-2.Поскольку односторонний критерий более "жестко" отвергает нулевую гипотезу, чем двусторонний, построим правостороннюю критическую область исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости a. P(c²>c²кр(a;k))=a.
Таким образом, правосторонняя область определяется неравенством c²>c²кр(a;k), а область принятия нулевой гипотезы – неравенством c²>c²кр(a;k).
Алгоритм применения критерия Пирсона.
1. Выдвигают нулевую гипотезу о нормальном законе распределения случайной величины X и находят его параметры xв и S.
2. Определяют теоретические частоты ni’, соответствующие опытным частотам. Если среди опытных частот имеются малочисленные, то их необходимо объединить с соседними. Интервалы после объединения будем обозначать (ai;bi]. Число интервалов должно быть не менее 4-х. Если случайная величина X непрерывна,
то  .
.
3. По формуле вычисляют величину.
4. Определяем число степеней свободы k= l-3, где l – число интервалов после объединения.
 .
.
5. Находят уровень значимости a=1-g, где g – доверительная вероятность; при g=0,95, g=0,05.

6. По таблице при заданных a и k находят значение
которое является критической точкой.
7. Если  , нет оснований отвергнуть нулевую гипотезу.
, нет оснований отвергнуть нулевую гипотезу.
Если 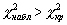 , нулевую гипотезу отвергают.
, нулевую гипотезу отвергают.
№68 Статистический коэффициент корреляции, Термин "корреляция" означает "связь". В эконометрике этот термин обычно используется в сочетании "коэффициенты корреляции". Рассмотрим линейный и непараметрические парные коэффициенты корреляции.
Обсудим способы измерения связи между двумя случайными переменными. Пусть исходными данными является набор случайных векторов  Выборочным коэффициентом корреляции, более подробно, выборочным линейным парным коэффициентом корреляции К. Пирсона, как известно, называется число
Выборочным коэффициентом корреляции, более подробно, выборочным линейным парным коэффициентом корреляции К. Пирсона, как известно, называется число
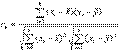
Если rn = 1, то 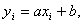 причем a>0. Если же rn = - 1, то
причем a>0. Если же rn = - 1, то 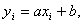 причем a<0. Таким образом, близость коэффициента корреляции к 1 (по абсолютной величине) говорит о достаточно тесной линейной связи.
причем a<0. Таким образом, близость коэффициента корреляции к 1 (по абсолютной величине) говорит о достаточно тесной линейной связи.
Если случайные вектора 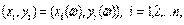 независимы и одинаково распределены, то выборочный коэффициент корреляции сходится к теоретическому при безграничном возрастании объема выборки:
независимы и одинаково распределены, то выборочный коэффициент корреляции сходится к теоретическому при безграничном возрастании объема выборки:
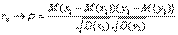
(сходимость по вероятности).
Более того, выборочный коэффициент корреляции является асимптотически нормальным. Это означает, что
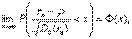
где 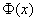 - функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1, а
- функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1, а 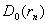 - асимптотическая дисперсия выборочного коэффициента корреляции. Она имеет довольно сложное выражение, приведенное в монографии [1, с.393]:
- асимптотическая дисперсия выборочного коэффициента корреляции. Она имеет довольно сложное выражение, приведенное в монографии [1, с.393]:
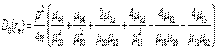
Здесь под  понимаются теоретические центральные моменты порядка k и m, а именно,
понимаются теоретические центральные моменты порядка k и m, а именно,
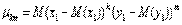 .
.
Коэффициенты корреляции типа rn используются во многих алгоритмах многомерного статистического анализа. В теоретических рассмотрениях часто считают, что случайные вектора 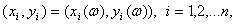 имеют двумерное нормальное распределение. Распределения реальных данных, как правило, отличны от нормальных (см. главу 2.1). Почему же распространено представление о двумерном нормальном распределении? Дело в том, что теория в этом случае проще. В частности, равенство 0 теоретического коэффициента корреляции эквивалентно независимости случайных величин. Поэтому проверка независимости сводится к проверке статистической гипотезы о равенстве 0 теоретического коэффициента корреляции. Эта гипотеза принимается, если
имеют двумерное нормальное распределение. Распределения реальных данных, как правило, отличны от нормальных (см. главу 2.1). Почему же распространено представление о двумерном нормальном распределении? Дело в том, что теория в этом случае проще. В частности, равенство 0 теоретического коэффициента корреляции эквивалентно независимости случайных величин. Поэтому проверка независимости сводится к проверке статистической гипотезы о равенстве 0 теоретического коэффициента корреляции. Эта гипотеза принимается, если 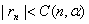 , где
, где  - некоторое граничное значение, зависящее от объема выборки n и уровня значимости
- некоторое граничное значение, зависящее от объема выборки n и уровня значимости 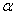 .
.
Если предположение о двумерной нормальности не выполнено, то из равенства 0 теоретического коэффициента корреляции не вытекает независимость случайных величин. Нетрудно построить пример случайного вектора, для которого коэффициент корреляции равен 0, но координаты зависимы. Кроме того, для проверки гипотез о коэффициенте корреляции нельзя пользоваться таблицами, рассчитанными в предположении нормальности. Можно построить правила принятия решений на основе асимптотической нормальности выборочного коэффициента корреляции. Но есть и другой путь – перейти к непараметрическим коэффициентам корреляции, одинаково пригодным при любом непрерывном распределении случайного вектора.
№ 69 Статистическая и регрессионная зависимость. Регрессионный анализ — это статистический метод исследования зависимости случайной величины у от переменных (аргументов) хj (j = 1, 2,..., k),рассматриваемых в регрессионном анализе как неслучайные величины независимо от истинного закона распределения xj.Обычно предполагается, что случайная величина у имеет нормальный закон распределения с условным математическим ожиданием 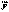 = φ(x1,..., хk),являющимся функцией от аргументов хj и с постоянной, не зависящей от аргументов дисперсией σ2.Для проведения регрессионного анализа из (k + 1)-мерной генеральной совокупности (у, x1, х2,..., хj,..., хk) берется выборка объемом n, и каждое i-е наблюдение (объект) характеризуется значениями переменных (уi, xi1, хi2,..., хij,..., xik), где хij — значение j-й переменной для i-го наблюдения (i = 1, 2,..., n), уi— значение результативного признака для i-го наблюдения.Наиболее часто используемая множественная линейная модель регрессионного анализа имеет вид
= φ(x1,..., хk),являющимся функцией от аргументов хj и с постоянной, не зависящей от аргументов дисперсией σ2.Для проведения регрессионного анализа из (k + 1)-мерной генеральной совокупности (у, x1, х2,..., хj,..., хk) берется выборка объемом n, и каждое i-е наблюдение (объект) характеризуется значениями переменных (уi, xi1, хi2,..., хij,..., xik), где хij — значение j-й переменной для i-го наблюдения (i = 1, 2,..., n), уi— значение результативного признака для i-го наблюдения.Наиболее часто используемая множественная линейная модель регрессионного анализа имеет вид  где βj — параметры регрессионной модели;εj — случайные ошибки наблюдения, не зависимые друг от друга, имеют нулевую среднюю и дисперсию σ2.
где βj — параметры регрессионной модели;εj — случайные ошибки наблюдения, не зависимые друг от друга, имеют нулевую среднюю и дисперсию σ2.
Отметим, что модель (53.8) справедлива для всех i = 1,2,..., n, линейна относительно неизвестных параметров β0, β1,…, βj, …, βk и аргументов. Как следует из (53.8), коэффициент регрессии Bj показывает, на какую величину в среднем изменится результативный признак у, если переменную хjувеличить на единицу измерения, т.е. является нормативным коэффициентом. В матричной форме регрессионная модель имеет ви  где Y — случайный вектор-столбец размерности п х 1 наблюдаемых значений результативного признака (у1, у2,.... уn); Х— матрица размерности п х (k + 1) наблюдаемых значений аргументов, элемент матрицы х,, рассматривается как неслучайная величина (i = 1, 2,..., n; j=0,1,..., k; x0i, = 1); β — вектор-столбец размерности (k + 1) х 1 неизвестных, подлежащих оценке параметров модели (коэффициентов регрессии); ε — случайный вектор-столбец размерности п х 1 ошибок наблюдений (остатков). Компоненты вектора εi не зависимы друг от друга, имеют нормальный закон распределения с нулевым математическим ожиданием (Mεi = 0) и неизвестной постоянной σ2 (Dεi = σ2). На практике рекомендуется, чтобы значение п превышало k не менее чем в три раза
где Y — случайный вектор-столбец размерности п х 1 наблюдаемых значений результативного признака (у1, у2,.... уn); Х— матрица размерности п х (k + 1) наблюдаемых значений аргументов, элемент матрицы х,, рассматривается как неслучайная величина (i = 1, 2,..., n; j=0,1,..., k; x0i, = 1); β — вектор-столбец размерности (k + 1) х 1 неизвестных, подлежащих оценке параметров модели (коэффициентов регрессии); ε — случайный вектор-столбец размерности п х 1 ошибок наблюдений (остатков). Компоненты вектора εi не зависимы друг от друга, имеют нормальный закон распределения с нулевым математическим ожиданием (Mεi = 0) и неизвестной постоянной σ2 (Dεi = σ2). На практике рекомендуется, чтобы значение п превышало k не менее чем в три раза 
В первом столбце матрицы Х указываются единицы при наличии свободного члена в модели (53.8). Здесь предполагается, что существует переменная x0,которая во всех наблюдениях принимает значения, равные единице.
Основная задача регрессионного анализа заключается в нахождении по выборке объемом п оценки неизвестных коэффициентов регрессии β0, β1, …, βkмодели (53.8) или вектора β в (53.9).
Так как в регрессионном анализе хj рассматриваются как неслучайные величины, a Mεi = 0, то согласно (53.8) уравнение регрессии имеет вид 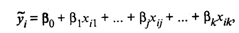 для всех i = 1, 2,..., п, или в матричной форме:
для всех i = 1, 2,..., п, или в матричной форме: 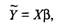 где
где 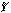 — вектор-столбец с элементами
— вектор-столбец с элементами 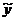 1...,
1..., 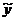 i,...,
i,..., 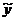 n.
n.
Для оценки вектора-столбца β наиболее часто используют метод наименьших квадратов, согласно которому в качестве оценки принимают вектор-столбец b,который минимизирует сумму квадратов отклонений наблюдаемых значений уi от модельных значений  i, т.е. квадратичную форму:
i, т.е. квадратичную форму: 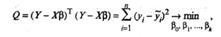 где символом «Т» обозначена транспонированная матрица.
где символом «Т» обозначена транспонированная матрица. 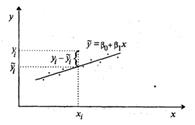 Дифференцируя, с учетом (53.11) и (53.10), квадратичную форму Q по β0, β1, …, βk и приравнивая частные производные к нулю, получим систему нормальных уравнений
Дифференцируя, с учетом (53.11) и (53.10), квадратичную форму Q по β0, β1, …, βk и приравнивая частные производные к нулю, получим систему нормальных уравнений
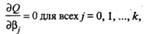
№ 70 Поле корреляции. Корреля́ция (от лат. correlatio — соотношение, взаимосвязь), корреляционная зависимость — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.[1]Математической мерой корреляции двух случайных величин служит корреляционное отношение 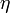 [2], либо коэффициент корреляции
[2], либо коэффициент корреляции 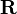 (или
(или  )[1]. В случае, если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической[3].Впервые в научный оборот термин «корреляция» ввёл французский палеонтолог Жорж Кювье в XVIII веке. Он разработал «закон корреляции» частей и органов живых существ, с помощью которого можно восстановить облик ископаемого животного, имея в распоряжении лишь часть его останков. В статистике слово «корреляция» первым стал использовать английский биолог и статистик Фрэнсис Гальтон в конце XIX века.[4]Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными. В первом случае предполагается, что мы можем определить только наличие или отсутствие связи, а во втором — также и её направление. Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой. При этом коэффициент корреляции будет отрицательным. Положительная корреляция в таких условиях — это такая связь, при которой увеличение одной переменной связано с увеличением другой переменной. Возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин.Значительная корреляция между двумя случайными величинами всегда является свидетельством существования некоторой статистической связи в данной выборке, но эта связь не обязательно должна наблюдаться для другой выборки и иметь причинно-следственный характер. Часто заманчивая прос
)[1]. В случае, если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической[3].Впервые в научный оборот термин «корреляция» ввёл французский палеонтолог Жорж Кювье в XVIII веке. Он разработал «закон корреляции» частей и органов живых существ, с помощью которого можно восстановить облик ископаемого животного, имея в распоряжении лишь часть его останков. В статистике слово «корреляция» первым стал использовать английский биолог и статистик Фрэнсис Гальтон в конце XIX века.[4]Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными. В первом случае предполагается, что мы можем определить только наличие или отсутствие связи, а во втором — также и её направление. Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой. При этом коэффициент корреляции будет отрицательным. Положительная корреляция в таких условиях — это такая связь, при которой увеличение одной переменной связано с увеличением другой переменной. Возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин.Значительная корреляция между двумя случайными величинами всегда является свидетельством существования некоторой статистической связи в данной выборке, но эта связь не обязательно должна наблюдаться для другой выборки и иметь причинно-следственный характер. Часто заманчивая прос
|
|
|


