Главная | Обратная связь | Поможем написать вашу работу!

Органы управления, индикации и подключения

На передней панели вольтметра (рис.2.4) расположены:

индикатор (поз. 1) для отображения значений измеряемых величин;

входные гнезда (поз. 2-5) для подключения вольтметра к измеряемому объекту;

переключатель рода работ и пределов измерений (поз. 6).

2.5. Методики измерений

2.5.1. Осциллографические измерения

2.5.1.1. Измерение постоянного напряжения

При измерении постоянного напряжения генератор развертки должен работать в режиме внутренней синхронизации.

Перед началом измерений следует тщательно установить нулевую линию осциллографа – линию, прочерчиваемую разверткой при отсутствии входного сигнала. Измеряемое напряжение подают на открытый вход канала А или канала Б (переключатель ┴ ~ — в положении ) осциллографа, а переключателем коэффициента отклонения V/ДЕЛ устанавливают луч в пределах экрана. Измеряют число делений, на которое переместился луч, и умножают это число на значение коэффициента отклонения.

2.5.1.2. Измерение переменного напряжения

Для измерения переменного напряжения сигнал подается на закрытый вход канала А или канала Б. Осциллограф в зависимости от характера измерений может работать в режиме внутренней или внешней синхронизации.

Переключатель коэффициента отклонения V/ДЕЛ выбранного канала ставится в такое положение, при котором размах осциллограммы исследуемого сигнала максимален и находится в пределах экрана. После осуществления синхронизации переключателем ВРЕМЯ/ДЕЛ выбирается такой коэффициент развертки, при котором на экране наблюдается несколько периодов исследуемого сигнала.

Амплитуда напряжения равна половине делений между крайними точками размаха осциллограммы, умноженного на показания переключателя V/ДЕЛ.

2.5.1.3. Измерение частоты

Частоту периодического сигнала находят путем измерения периода его повторения. Для этого по осциллограмме измеряют расстояния между точками, соответствующими периоду сигнала, умножают его на показания переключателя коэффициента развертки и находят обратную величину.

2.5.1.4. Измерение сдвига фаз

Сдвигом фаз (фазовым сдвигом) φ называется разность начальных фаз двух гармонических сигналов одинаковой частоты u ₁(t) = U ₁_m sin (w t +j₁) и
u ₂(t) = U ₂_m sin (w t +j₂):

j = j₁ - j₂.

Для измерения сдвига фаз на вход канала А подают первый сигнал, относительно которого измеряется сдвиг фазы второго сигнала (так называемый опорный сигнал), а на вход канала Б – второй (сравниваемый сигнал). В результате на экране осциллографа при совмещении нулевых линий развертки обоих каналов наблюдаются осциллограммы, подобные осциллограммам, приведенным на рис.5.

Измерив интервал времени DT между моментами, когда сигналы находятся в одинаковых фазах, например нулевых, и период следования Т одного из сигналов и соотнося этот период с интервалом DT, получим:

На рис.2.5,а величина D T измеряемая относительно точки нулевой фазы сигнала U ₁ (точка 0), положительна. Это свидетельствует о задержке второго сигнала относительно первого. Поэтому сдвигу фаз следует приписать знак, минус. Если второй сигнал по времени опережает первый (рис.2.5,б), то сдвиг фаз является положительным.

Рис. 2.5. Осциллограммы сигналов со сдвигом фаз

2.5.2. Снятие амплитудно-частотных и фазо-частотных характеристик

Амплитудно-частотные и фазо-частотные характеристики линейной системы определяют из анализа колебаний, имеющих место на выходе системы при воздействии на ее вход гармонического сигнала.

Для снятия зависимости модуля коэффициента передачи по напряжению от частоты (АЧХ) устанавливают на входе системы некоторое напряжение U _ВХ, которое при всех последующих измерениях поддерживают постоянным.

Затем последовательно через некоторый интервал изменяют частоту этого напряжения и измеряют соответствующее напряжение на выходе системы. Полученные отношения U _ВЫХ(f _i)/ U _ВХ(f _i) наносят в виде точек на плоскости в прямоугольной системе координат K, f и соединяют эти точки плавной кривой.

Аналогичным образом снимают ФЧХ, представляющей собой зависимость от частоты входного сигнала сдвига фаз между выходным и входным гармоническими сигналами.

Диапазон частот, в котором необходимо проводить измерения, зависит от конкретной линейной системы.

2.5.3. Измерение входного сопротивления
электронных устройств

Входное сопротивление электронных устройств – это их сопротивление со стороны входных зажимов. Измерения проводят на переменном токе. При измерении активной составляющей входного сопротивления, измерения следует проводить на частотах, на которых входной емкостью устройства можно пренебречь.

Схема для измерения входного сопротивления показана на рис.2.6.

Когда выходные зажимы генератора непосредственно (без резистора R) подключены к входным зажимам устройства, напряжение U_вх на входном сопротивлении R _вх: U _ВХ = U _Г.

При подключении резистора R напряжение на входных зажимах уменьшается и становится равным .

Решив эти два уравнение, получим:

Полученное выражение справедливо лишь в том случае, когда в качестве источника сигнала используется источник напряжения, т.е. если выходное сопротивление генератора (на рис.2.6 не показано) много меньше R и R _ВХ. В противном случае необходимо измерять напряжения U _вх и при одинаковом напряжении на выходе генератора.

Таким образом, для измерения входного сопротивления следует измерить напряжение на входе устройства при непосредственной подаче напряжения генератора и при подаче напряжения через резистор с известным сопротивлением.

2.5.4. Измерение выходного сопротивления
электронных устройств

Выходное сопротивление электронного устройство – сопротивление этого устройства со стороны выходных зажимов.

Структурная схема измерения выходного сопротивления приведена на рис.2.7. На этом рисунке устройство, выходное сопротивление которого измеряется, представлено эквивалентной схемой в виде генератора напряжения. Для измерения выходного сопротивления сначала измеряется выходное напряжение устройства при так называемом холостом ходе, т.е. без подключения к устройству нагрузки, а затем измеряется напряжение на выходе при подключенной нагрузке (резисторе с известным сопротивлением).

Рис. 2.7. Схема измерения выходного сопротивления электронного устройства

При отключенном сопротивлении нагрузки R_Н (режим холостого хода) выходное напряжение .

Когда нагрузка подключена, выходное напряжение уменьшается и становится равным .

Решив эти уравнения, получим:

Для получения хорошей точности измерений следует брать сопротивление нагрузки, соизмеримое с выходным сопротивлением устройства.

3. Задания и методические рекомендации

3.1. Подготовка осциллографа к работе

3.1.1. Ознакомьтесь с расположением органов управления осциллографом.

3.1.2. Поставьте органы управления в следующие исходные положения:

- тумблер "СЕТЬ" в положение выключено;

- ручку "ЯРКОСТЬ" в среднее положение;

- ручку "ФОКУС" в среднее положение;

- переключатели коэффициентов отклонения "V/ДЕЛ" каналов А и Б в положение 1 V/ДЕЛ;

- переключатель для выбора автоколебательного или ждущего режима развертки в положение АВТ;

- переключатель для включения и выключения каналов А и Б в положение, обеспечивающее двухканальный режим работы;

- переключатель "ВРЕМЯ/ДЕЛ." в положение 1 мс/ДЕЛ;

- переключатель x l; х 0,1 в положение xl;

- ручки перемещения луча по горизонтали в среднее положение.

3.1.3. Включите переключатель "СЕТЬ" и дайте осциллографу прогреться в течение 1-2 минут.

3.1.4. По наблюдаемой на экране осциллографа линии развертки отрегулируйте яркость луча и произведите его фокусировку.

3.1.5. Переведите последовательно переключатель "ВРЕМЯ/ДЕЛ" в сторону больших значений коэффициента развертки вплоть до верхнего предела. Наблюдайте перемещение луча осциллографа все с меньшей скоростью.

3.1.6. Проверьте калибровку коэффициентов отклонения канала А.осциллографа. Для этого подайте на его вход сигнал с выхода калибратора осциллографа, который представляет собой последовательность калиброванных по амплитуде и частоте следования импульсов. Значения амплитуды и частоты указаны возле выхода калибратора. Медленно вращая потенциометр "УРОВЕНЬ" получите на экране устойчивое изображение осциллограммы сигнала. Измерьте амплитуду импульсов.

3.1.7. Повторите пункт 3.1.6 для канала Б.

3.1.8. Проверьте калибровку коэффициентов развертки "ВРЕМЯ/ДЕЛ". Для этого подайте на вход канала А (канала Б) тот же сигнал с калибратора. С помощью переключателя "ВРЕМЯ/ДЕЛ" растяните изображение на экране так, чтобы наблюдалось несколько периодов сигнала, измерьте период следования импульсов и по нему определите частоту. Сравните ее с частотой калибровочного сигнала.

3.2. Измерение параметров сигналов

3.2.1. Включите ГНЧ и дайте ему прогреться в течение 1 минуты. Установите частоту сигнала 1 кГц.

3.2.2. Установите переключатель для выбора автоколебательного или ждущего режима развертки в положение АВТ, переключатель для включения и выключения каналов А и Б в положение, обеспечивающее одноканальный режим работы (канал А), переключатель «А СЕТЬ ВНЕШН Б» в положение, обеспечивающее синхронизацию развертки осциллографа сигналом канала А.

3.2.3. Подайте на вход канала А осциллографа сигнал с выхода ГНЧ. В качестве элемента соединения выхода генератора и входа осциллографа используйте клеммы, расположенные слева от резистора R 5 (модуль №1).

3.2.4. Используя ступенчатый аттенюатор и ручку плавной регулировки амплитуды ГНЧ, установите на экране осциллографа изображение, размах которого занимает практически всю рабочую часть экрана.

3.2.5. Плавно вращая ручку “УРОВЕНЬ”, получите на экране устойчивое изображение осциллограммы.

Отсоедините вход осциллографа от выхода ГНЧ. Обратите внимание на то, что линия развертки на экране сохраняется. Это является характерным признаком периодической развертки при автоколебательном режиме работы генератора развертки.

3.2.6. Измерьте амплитуду гармонического сигнала, приходящего с ГНЧ, вольтметром и осциллографом. Объясните разницу результатов измерений.

3.2.7. Измерьте частоту сигнала, предварительно определив его период, и сравните его с показаниями индикаторного табло ГНЧ.

3.2.8. Установите переключатель для включения и выключения каналов А и Б в положение, обеспечивающее двухканальный режим работы.

3.2.9. Подайте на вход канала Б осциллографа сигнал с выхода ГНЧ. В качестве элемента соединения выхода генератора и входа осциллографа используйте клеммы, расположенные справа от резистора R5 (модуль №1). Измерьте амплитуду гармонического сигнала.

3.2.10. Подайте на вход канала А осциллографа сигнал с нижнего выхода генератора сигналов (модуль №1), на вход канала Б осциллографа сигнал с верхнего выхода генератора сигналов, гнезда 2 и 3 генератора сигналов соедините перемычкой (рис. 3.1).

Наблюдайте осциллограммы сигналов при периодической и ждущей развертках. Зарисуйте осциллограммы при запуске генератора развертки по фронту и спаду импульсов. Измерьте амплитуду сигналов, длительность прямоугольных импульсов, период их следования и рассчитайте скважность, измерьте длительность участков пилообразных импульсов с нарастающим и спадающим напряжением.

Обратите внимание на переключатели входов канала А и канала Б осциллографа. Одно положение переключателя соответствует закрытому (для постоянной составляющей) входу, второе – открытому. Сигнал с генератора сигналов модуля №1 содержит постоянную составляющую. Подавая его через открытый и закрытый вход, убедитесь, что в первом случае осциллограмма смещается вниз на величину постоянной составляющей.

3.3. Изучение аттенюатора напряжения

Аттенюатор напряжения, содержащийся в модуле №1 (рис. 3.2) предназначен для ослабления сигнала в 10, 100 и 1000 раз, а также для получения источника сигналов с низким выходным сопротивлением. Он представляет собой обычный резистивный делитель напряжения, дополненный усилителем У1 с единичным коэффициентом усиления и низким выходным сопротивлением.

Рис. 3.2. Схема аттенюатора

3.3.1. Подайте с ГНЧ на вход аттенюатора 1:1 гармонический сигнал частотой 1 кГц и амплитудой 1 В. Измерьте амплитуду сигнала на выходе аттенюатора.

Измерьте входное и выходное напряжения вольтметром.

Сравните результаты измерения входного и выходного напряжений аттенюатора осциллографом и вольтметром. Объясните их.

Проделайте то же самое, подавая сигнал на входы 1:10 и 1:100.

3.3.2. Измерьте выходное сопротивление ГНЧ. В качестве сопротивления нагрузки возьмите резистор R5 (см. модуль № 1). Амплитуду сигнала на выходе ГНЧ установите равной 1 В, частоту – 1 кГц.

Выходное сопротивление находится из выражения:

3.3.3. Подайте сигнал с генератора на вход 1:1 аттенюатора и измерьте выходное сопротивление аттенюатора. Резистор нагрузки возьмите тот же.

Измерьте аналогично выходное сопротивление аттенюатора при подаче сигнала на вход 1:10.

Убедитесь в том, что выходное сопротивление аттенюатора меньше выходного сопротивления генератора.

3.4. Измерение сдвига фаз между гармоническими сигналами

3.4.1. Соберите схему согласно рис.3.3 и установите на выходе ГНЧ сигнал с амплитудой 2 В и частотой 16 кГц.

3.4.2. Установите линии развертки каналов А и Б точно в центре масштабной сетки экрана. В дальнейшем ручкой перемещения луча по вертикали не пользуйтесь. Переведите соответствующим переключателем осциллограф в режим синхронизации сигналом, поступающим на вход канала А.

4.4. Наблюдайте осциллограммы сигналов на входе RC-цепи и на ее выходе. Определите по ним величины Δ Т и Т (Рис. 5) и рассчитайте сдвиг фаз между выходным и входным сигналами RC-цепи. Поскольку момент пересечения нулевой линии выходным сигналом наступает позже момента пересечения этой линии входным сигналом, то величина Δ Т является отрицательной и

3.5. Измерение входного сопротивления осциллографа

3.5.1. Подайте на вход осциллографа через резистор R6 (модуль №1) сигнал с ГНЧ амплитудой 1 В и частотой 1 кГц.

3.5.2. Измерьте сигнал на выходе ГНЧ и по формуле

рассчитайте входное сопротивление осциллографа.

4. Отчет

В отчет необходимо включить:

· цель лабораторной работы;

· все схемы измерений и результаты измерений;

· осциллограммы исследуемых сигналов;

· результаты, полученные при измерении сдвига фаз между гармоническими сигналами, при измерении входного и выходного сопротивлений электронных устройств;

· выводы.

5. Вопросы и задания для самопроверки

· Каково назначение функциональных узлов электронного осциллографа?

· Какое содержание вкладывается в термин «синхронизация осциллографа»?

· Поясните, каким образом с помощью осциллографа можно определить частоту переменного напряжения?

· Поясните методику измерения входного сопротивления электронного устройства.

· Каким образом можно измерить выходное сопротивление электронного устройства?

· Как с помощью осциллографа можно измерить сдвиг фаз между гармоническими сигналами?

6. Литература

1. Морозов А.Г. Электротехника, электроника и импульсная техника: Учеб. Пособие для инженерно-эконом. спец. вузов. – М.: Высш. Шк., 1987. -448с.

2. Электротехника и электроника: Учебник для сред. проф. образования/Б.И. Петленко, Ю.М. Иньков, А.В. Крашенинников и др.; Под ред. Б.И. Петленко. – М.; Издательский центр «Академия», 2003. – 320 с.

Лабораторная работа №2.
ПРЕОБРАЗОВАНИЕ СИГНАЛОВ ЛИНЕЙНЫМИ СИСТЕМАМИ С ПОСТОЯННЫМИ ПАРАМЕТРАМИ

Используемые модули: №№ 1, 3, 4, 13

1. Цель лабораторной работы

Цель лабораторной работы:

· изучить основные свойства RC-цепей интегрирующего и дифференцирующего типа;

· изучить основные свойства последовательного колебательного контура;

· изучить влияния сопротивления потерь на добротность последовательного колебательного контура, на его полосу пропускания и на его переходную характеристику;

· снять амплитудно-частотные и фазо-частотные характеристики простейших линейных систем;

· снять переходные характеристики простейших линейных систем.

2. Сведения из теории

Анализ линейных цепей можно проводить в частотной или во временной области. Анализ во временной области позволяет выяснить изменение формы входного сигнала. В частотной области этот результат будет выглядеть как преобразование над функцией частоты, приводящее к изменению спектрального состава входного сигнала, которое в конечном итоге определяет форму выходного сигнала.

Характеристики простейших линейных цепей в частотной и во временной области представлены в табл.2.1.

2.1. Цепи интегрирующего типа (фильтры нижних частот)

Интегрирующей называется цепь, выходной сигнал которой пропорционален интегралу входного сигнала. Выходное напряжение (при нулевых начальных условиях U_вых (0) = 0) RC-цепи, представленной на рис. 2.1, а,

где – выражаемая определенным интегралом алгебраическая (т.е. с учетом знака) площадь под сигналом на интервале (0,t), – результат точного интегрирования сигнала.

Величина обратно пропорцио-нальна величине t =
= RC, которая получила название постоянной времени RC -цепи. Следовательно, для возможности исполь-зования RC -цепи в качестве интегри-рующей необходимо, чтобы постоянная времени t была достаточно велика. Поэтому эта цепь называется RC -цепью интегрирующего типа.

Комплексный коэффициент передачи RC -цепи интегрирующего типа

Отсюда амплитудно-частотная характеристика (АЧХ) и фазо-частотная характеристика (ФЧХ) . Переходная характеристика RC - цепи интегрирующего типа .

Вид АЧХ RC -цепи интегрирующего типа (рис 2.1,б) показывает, что мы имеем дело с цепью, эффективно пропускающей низкие частоты. Поэтому RC -цепь такого типа можно классифицировать как фильтр нижних частот (ФНЧ). При соответствующем выборе постоянной времени можно существенно ослабить (отфильтровать) высокочастотные составляющие входного сигнала и практически выделить постоянную составляющую (если она имеется). За граничную частоту такого фильтра принимают частоту, на которой 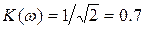, т.е. коэффициент передачи мощности сигнала снижается в 2 раза. Ее часто называют частотой среза w_с (верхней граничной частотой). Частота среза .

Фазовый сдвиг, вносимый RC -цепью интегрирующего типа на частоте w_с, составляет –p/4.

К цепям интегрирующего типа относится также LR -цепь с сопротивлением на выходе (рис. 2.1. б). Постоянная времени такой цепи t = L/R.

2.2. Цепи дифференцирующего типа (фильтры верхних частот)

Дифференцирующей называется цепь, выходной сигнал которой пропорционален производной входного сигнала.

Выходной сигнал RC -цепи, представленной на рис. 2.2, а,

При условии выходной сигнал . Поэтому рассматриваемая цепь называется RC -цепью дифференцирующего типа.

Комплексный коэффициент передачи RC -цепи дифференцирующего типа АЧХ и ФЧХ (рис. 2.2, в) даются соответственно выражениями:

Переходная характеристика RC -цепи дифференцирующего типа

Характер поведения АЧХ RC -цепи дифференцирующего типа показывает, что такая цепь эффективно пропускает высокие частоты, поэтому ее можно классифицировать как фильтр верхних частот (ФВЧ). За граничную частоту такого фильтра принимают частоту, на которой . Ее часто называют частотой среза w_с (нижней граничной частотой). Частота среза

При больших постоянных времени τ RC -цепи дифференцирующего типа напряжение на резисторе повторяет переменную составляющую входного сигнала, а его постоянная составляющая полностью подавляется. RC -цепь в этом случае называется разделительной.

Такими же характеристиками обладает RL -цепь на рис.2.2,б с постоянной времени τ = L/R.

2.3. Частотно-избирательные цепи

Частотно-избирательные цепи пропускают на выход только колебания с частотами, лежащими в относительно узкой полосе вокруг центральной частоты. Такие цепи часто называют линейными полосовыми фильтрами. Простейшими полосовыми фильтрами являются колебательные контуры, образованные элементами L и C.

Колебательные контуры в зависимости от соединения образующих их элементов по отношению к выходным зажимам подразделяются на последовательные и параллельные.

Схема последовательного колебательного контура, когда выходным сигналом является напряжение, снимаемое с конденсатора, приведена на рис.2.3, а. В приведенной на этом рисунке схеме сопротивление R представляет собой активное сопротивление индуктивности.

Комплексный коэффициент передачи такого контура

Отсюда АЧХ и ФЧХ АЧХ и ФЧХ даются соответственно выражениями:

Если в последовательном колебательном контуре напряжение снимать с индуктивности (рис. 2.3, б), то

На некоторой частоте входных колебаний в последовательном колебательном контуре имеет место резонанс напряжений, выражающийся в том, что реактивные сопротивления конденсатора и индуктивности становятся равными по величине и противоположными по знаку. При этом общее сопротивление контура становится чисто активным, а ток в контуре имеет максимальное значение. Частоту, удовлетворяющую условию называют резонансной частотой w₀. Она определяется выражением

Модуль сопротивления любого из реактивных элементов колебательного контура на резонансной частоте называется характеристическим (волновым) сопротивлением контура.

Отношение активного сопротивления к характеристическому сопротивлению называют затуханием контура:

Обратную d величину именуют добротностью контура:

На резонансной частоте

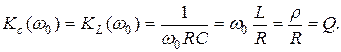
Это означает, что напряжение на каждом из реактивных элементов контура при резонансе в Q раз превосходит напряжение источника сигнала.

Используя введенные w₀ и Q, можно записать:

При нахождении добротности реального (включенного в какую-либо цепь) последовательного колебательного контура необходимо учитывать внутреннее (выходное) сопротивление R_с источника входного сигнала (это сопротивление будет включаться последовательно с активным сопротивлением контура) и активное сопротивление R_н нагрузки (которое окажется подключенным параллельно выходному реактивному элементу). С учетом этого эквивалентная добротность

Отсюда следует, что резонансные свойства последовательного колебательного контура лучше всего проявляются при низкоомных источниках сигнала и при высокоомных нагрузках.

Полоса пропускания колебательного контура вводится аналогично полосе пропускания RC -цепей 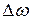= w _В- w _Н(рис. 2.4), т.е. как область частот, в пределах которой модуль комплексного коэффициента передачи не снижается ниже уровня от максимального (при резонансе) значения.

Полоса пропускания контура где

Переходная характеристика колебательного контура при больших значениях добротности Q определяется выражением

удельный вес в электротехнике, в разработке, исследовании и эксплуатации устройств промышленной электроники. Это связано с тем, что расчеты многих устройств дают лишь ориентировочные данные, а реальные режимы работы и оптимальные параметры можно установить только на основании эксперимента. Исследование же устройств промышленной электроники и их эксплуатация вообще немыслимы без измерительной аппаратуры, так как без нее невозможен не только количественный, но и качественный анализ интересующих нас явлений.

3. Задания и методические рекомендации

3.1. Исследование RC -цепи интегрирующего типа
(фильтра нижних частот)

3.1.1. Соберите схему согласно рис.3.1 и снимите АЧХ RC -цепи интегрирующего типа, состоящей из элементов R 2 и C 1 (модуль № 4).

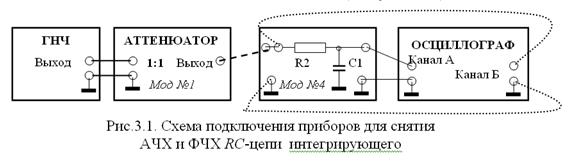
Амплитуда входного сигнала может быть произвольной, поскольку цепь линейна и пассивна. С целью упрощения расчетов целесообразно амплитуду взять равной 1 B. Измерения проводите на частотах, указанных в табл.3.1. Результаты измерений заносите в табл.3.1.

Таблица 3.1

f,кГц

0,1

0,5

U вх,B

U вых,B

K (f)

Δ T

φ,град

3.1.2. Постройте АЧХ и определите из графика частоту среза ƒс, по которой найдите постоянную времени цепи τ. Сравните полученное значение τ с расчетным значением τрасч = R 2 C 1.

3.1.3. Снимите ФЧХ этой же RC -цепи. Результаты измерений заносите в табл.3.1.

3.1.4. Постройте ФЧХ и определите по ней постоянную времени цепи τ. Сравните ее с полученной ранее из АЧХ.

3.1.5. Получите переходную характеристику исследуемой цепи. Для этого на вход аттенюатора с выхода ГНЧ подайте прямоугольные импульсы. Частоту следования этих импульсов и длительность развертки осциллографа установите такими, чтобы на экране было изображение реакции цепи на один скачок напряжения.

Зарисуйте переходную характеристику и из нее определите постоянную времени цепи как интервал времени, за который выходное напряжение достигает уровня 0,63 от максимального.

Сравните значение постоянной времени со значениями постоянной времени, полученными из АЧХ и ФЧХ.

3.1.6. Получите переходную характеристику RC -цепи интегрирующего типа из элементов R 1 и C 1 модуля №4. Изобразите ее на том же графике, где была зарисована переходная характеристика предыдущей цепи. С чем связано изменение переходной характеристики? Как будут выглядеть АЧХ и ФЧХ такой цепи?

3.2. RC -цепи дифференцирующего типа (фильтры верхних частот)

3.2.1. Соберите схему согласно рис.3.2 и снимите АЧХ RC -цепи дифференцирующего типа, состоящей из элементов R 6 и C 5 модуля №4.

Измерения проводите на частотах, указанных в табл.3.2. Результаты измерений заносите в табл.3.2.

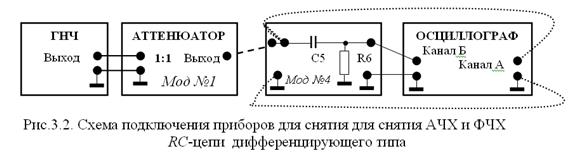
Таблица 3. 2

f,кГц

0,2

0,5

Uвх,B

Uвых,B

K(f)

ΔT

φ, град

3.2.2.Постройте АЧХ и определите из нее частоту среза f _c и постоянную времени τ. Сравните полученное значение τ с расчетным.

3.2.3. Снимите ФЧХ исследуемой цепи. Результаты измерений заносите в табл.3.2.

3.2.4. Постройте ФЧХ и определите по ней постоянную времени цепи τ. Сравните ее с полученной ранее из АЧХ.

3.2.5. В соответствии с п.3.1.5 получите переходную характеристику исследуемой цепи, зарисуйте ее и определите по ней постоянную времени t как интервал времени, за который выходное напряжение достигает уровня 0,37 от максимального.

Сравните значения τ, полученные из АЧХ, ФЧХ и переходной характеристики.

3.2.5. Получите переходную характеристику RC -цепи дифференцирующего типа из элементов R 6 и C 6 модуля №4. С чем связано ее изменение по сравнению с характеристикой предыдущей цепи? Как будет выглядеть ее АЧХ и ФЧХ?

3.3. Исследование последовательного колебательного контура

3.3.1. Запустите программу Electronics Workbench. Соберите схему для исследования последовательного колебательного контура (рис.3.3).

Рассчитайте значение индуктивности L 1 катушки индуктивности для случая резонансной частоты f ₀= 250 кГц (С 1 = 1нФ), волновое сопротивление ρ контура, его затухание d (для случая сопротивления потерь R 1 = 10 Ом) и добротность Q по формулам:

3.3.2. Получите АЧХ и ФЧХ исследуемого контура. По АЧХ определите резонансную частоту f _0и, полосу пропускания Δ f _и и рассчитайте добротность контура Q _и. Сравните полученные значения с расчетными.

3.3.3. Установите генератор испытательных сигналов в режим формирования положительных прямоугольных импульсов с частотой f =500 Гц, скважностью q = 2 и амплитудой U _п = 1 В.

3.3.4. Получите осциллограмму переходной характеристики исследуемого контура и определите по этой характеристике частоту свободных колебаний f _сви, сравните ее с резонансной частотой.

3.3.5. Повторите пункты 3.3.3 и 3.3.4 для резонансного контура с сопротивлением потерь R 1 = 1 Ом. Сопоставьте результаты, полученные в пунктах 3.3.3, 3.3.4 и 3.3.5.

4. Отчет

В отчет необходимо включить:

· цель лабораторной работы;

· схемы подключения приборов для исследования линейных цепей;

· таблицы экспериментальных значений;

· амплитудно-частотные и фазо-частотные характеристики, построенные по экспериментальным данным;

· полученные из АЧХ и ФЧХ значения граничных частот и постоянных времени исследуемых линейных систем;

· полученные из переходных характеристик значения постоянных времени исследуемых линейных систем;

· заданное значение резонансной частоты f ₀ колебательного контура, формулы и рассчитанные по ним параметры L 1, ρ, d, Q;

· АЧХ и ФЧХ, измеренные по ним резонансную частоту f _0и, полосу пропускания Δ f _и и добротность Q _и колебательного контура;

· осциллограммы переходных характеристик колебательного контура и вычисленные по ним частоты f_сви свободных колебаний;

· выводы.

5. Вопросы и задания для самопроверки

· Какая характеристика связывает между собой временные представления входного и выходного сигналов линейной системы?

· Какая характеристика связывает между собой спектральные представления входного и выходного сигналов линейной системы?

· Дайте определение импульсной и переходной характеристик.

· Дайте определение комплексного коэффициента передачи.

· Что показывает АЧХ и ФЧХ линейных систем?

· Дайте определение полосы пропускания линейной цепи.

· Почему RC-цепь интегрирующего типа можно классифицировать как фильтр нижних часто

⇐ Предыдущая 1 23

Воспользуйтесь поиском по сайту: