Распределения СВ.Распределение Пирсона.

РаспределениеПирсона — непрерывное распределение вероятностей, плотность вероятности которого является решением дифференциального
уравнения {\displaystyle {\frac {df(x)}{dx}}={\frac {a_{1}x+a_{0}}{b_{0}+2b_{1}x+b_{2}x^{2}}}f(x)}, где числа {\displaystyle a_{0},a_{1},b_{0},b_{1},b_{2}}являются параметрами распределения. Частными случаями распределения Пирсона являются бета распределение (распределениеПирсона I типа), гамма-распределение (распределениеПирсона III типа), распределение Стьюдента (распределениеПирсона VII типа), показательное распределение (распределение Пирсона X типа), нормальное распределение (распределение Пирсона XI типа). Распределения Пирсона широко используются в математической статистике при сглаживании распределений эмпирических данных. Для аппроксимации распределения вероятностей опытных данных численными методами вычисляют их первые четыре момента, а за тем на их основе вычисляют параметры распределения Пирсона. С помощью нормального распределения определяются три распределения, которые в настоящее время часто используются при статистической обработке данных. В дальнейших разделах книги много раз встречаются эти распределения.

Распределение Пирсона (хи - квадрат) –распределение случайной величины

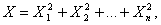
где случайные величины X₁, X₂,…, X_n независимы и имеют одно и тоже распределение N (0,1). При этом число слагаемых, т.е. n, называется «числом степеней свободы» распределения хи–квадрат.

4. РаспределенияСВ. РаспределениеСтьюдента

Распределе́ние Стью́дента- это одно параметрическое семейство абсолютно непрерывных распределений. Названо в честь Уильяма Сили Госсета, который первым опубликовал работы, посвящённые этому распределению, под псевдонимом«Стьюдент».

Распределение Стьюдента играет важную роль в некоторых широко используемых системах статистического анализа. Пример такой системы, t -критерий Стьюдента для оценки статистического значения разницы между двумя выборочными средними, построения доверительных интервалов разницы между двумя доверительными средними, а также в линейном регрессионном анализе. Распределение Стьюдента так же появляется в байесовском анализе данных, распределенных по нормальному закону.

Распределение Стьюдента может быть использовано для оценки того, насколько вероятно, что истинное среднее находится в каком-либо заданном диапазоне.

График плотности распределения Стьюдента, как инормального распределения, является симметричными колоколо-образным, но с более тяжелыми хвостами, из-за этого, величины с распределением Стьюдента чаще сильно отличаются от математического ожидания.

Распределение Стьюдента —частный случай обобщенного гиперболического распределения.

Распределение t Стьюдента–этораспределениеслучайнойвеличины

где случайные величины U и X независимы, U имеет распределение стандартное нормальное распределение N (0,1), а X – распределение хи–квадрат с n степенями свободы. При этом n называется«числом степеней свободы»распределения Стьюдента.

Распределение Стьюдента было введенов 1908 г. английским статистиком В. Госсетом, работавшем на фабрике, выпускающей пиво. Вероятностно-статистические методы использовались для принятия экономических и технических решений на этой фабрике, поэтому ее руководство запрещало
В. Госсету публиковать научные статьи под своим именем. Таким способом охранялась коммерческая тайна, «ноу-хау» в виде вероятностно-статистических методов, разработанных В. Госсетом. Однако они мел возможность публиковаться под псевдонимом «Стьюдент». История Госсета - Стьюдента показывает, что еще сто лет назад менеджерам Великобритании была очевидна большая экономическая эффективность вероятностно-статистических методов.

В настоящее время распределение Стьюдента–одно из наиболее известных распределений среди используемых при анализе реальных данных. Его применяют при оценивании математического ожидания, прогнозного значения и других характеристик с помощью доверительных интервалов, по проверке гипотез о значениях математических ожиданий, коэффициентов регрессионной зависимости.