 |
Решение задач с использованием пакета SPSS
|
|
|
|
Федеральное государственное образовательное бюджетное учреждение
Высшего образования
«Финансовый университет при Правительстве Российской Федерации»
(Финуниверситет)
Смоленский филиал Финуниверситета
Кафедра Математики и информатики
КОМПЬЮТЕРНЫЙ ПРАКТИКУМ
по дисциплине
ЭКОНОМЕТРИКА
Интерактивное занятие
для студентов третьего курса
направления 38.03.01 «Экономика»
(программа подготовки бакалавров)
Заочная форма обучения
2015 г.
Данное интерактивное практическое занятие на ПК имеет следующие цели:
· формирование у студентов умения самостоятельно осуществлять построение в среде EXCEL моделей парной и множественной регрессии и применять их для анализа и прогнозирования экономических процессов;
· проверка степени усвоения студентами лекционного материала по теме парной и множественной регрессии и применение полученных знаний для решения практических задач;
· формирование у студентов убежденности в необходимости освоения данной дисциплины с целью дальнейшего использования приобретенных знаний в практической деятельности.
Задачи занятия:
· формирование у студентов теоретических знаний по вопросам выбора факторных признаков и уяснение основных этапов построения моделей парной и множественной регрессии;
· получение студентами практических навыков при определении параметров регрессионных моделей;
· получение теоретических знаний и практических навыков при оценке качества уравнений регрессии;
· уяснение связи проблемы спецификации модели с ее качеством и возможностью использования для прогнозирования;
· получение студентами практических навыков для выполнения лабораторной и контрольной работ по темам парной и множественной регрессии.
|
|
|
Введение
Одним из главных направлений эконометрического анализа является построение моделей парной и множественной регрессий, обладающих высоким качеством, с целью дальнейшего их использования для анализа и прогнозирования развития экономических процессов. Эта проблема в значительной степени зависит от правильной спецификации модели, которая в дальнейшем определяет все свойства теоретической модели и возможность ее использования для построения прогнозов.
Построение регрессионной модели является творческим процессом, опирающимся на серьезные знания в области экономической теории, макро- и микроэкономики, эконометрического анализа и должно быть индивидуально в каждой конкретной ситуации.
Данный компьютерный практикум поможет студентам получить практические навыки по типовой процедуре построения моделей парной и множественной регрессии, выбору факторных признаков, оценке параметров и качеству моделей, построению прогнозов экономических процессов.
Компьютерный практикум состоит из трех заданий:
- в первой задаче по теме «Парная регрессия» студентам предлагается познакомиться с особенностями построения простейших однофакторных (линейных и нелинейных) регрессионных моделей, уяснить основные направления оценки качества моделей парной регрессии и использования их для целей прогнозирования экономических процессов.
Эти знания, несомненно, помогут студентам при освоении следующей темы, касающейся построения, анализа качества и прогнозирования по модели множественной регрессии.
- во второй задаче изложена типовая процедура выбора ведущего фактора из множества факторных признаков и построения линейной модели парной регрессии с целью дальнейшего расчета характеристик модели и определения прогноза результативного признака;
|
|
|
- в третьей задаче по теме «Множественная регрессия» рассмотрены основные этапы спецификации модели множественной регрессии, такие как, определение наличия и устранение мультиколлинеарности, расчет параметров и различных характеристик качества модели и построение прогнозов признаков.
Компьютерный практикум выполняется с использованием программных продуктов EXCEL и SPSS.
Необходимо также отметить важность освоения тем «Парная регрессия» и «Множественная регрессия» ввиду возможности и целесообразности использования практических аспектов данных тем при написании студентами выпускных квалификационных работ, а также в своей практической деятельности.
Задача 1
В качестве показателей, характеризующих результаты финансово-хозяйственной деятельности предприятия, могут быть выбраны:
· Объем выпуска продукции (Y, млн.руб.)
· Объем капиталовложений (X, млн.руб.)
Требуется:
1. Для характеристики зависимости объема выпуска продукции от объема капиталовложений построить следующие модели:
· Линейную;
· Экспоненциальную;
· Гиперболическую.
2. Результаты расчетов отразить на графике.
3. Выбрать лучшую по качеству модель. Ответ обосновать.
| Y | |||||||
| X |
Решение
I. Для построения модели линейной парной регрессии y=a+b*x
воспользуемся встроенной статистической функцией ЛИНЕЙН.
Для этого необходимо:
1) Создайте новый лист Excel (щелчок правой кнопкой на рабочем столе=>Создать=>Лист Microsoft Excel)
2) Введите исходные данные в соответствии с вариантом

Рис.1. Ввод исходных данных
3) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца)
4) Выберите в главном меню Вставка =>Функция
5) В меню Категория выберите Статистические в окне выбора функций – функцию ЛИНЕЙН, нажмите OK (Рис.2)

Рис.2. Окно выбора линейной функции
6) Заполните аргументы функции
Ø Значения Y- диапазон, содержащий значения результативного признака (нажать кнопку в правой части соответствующей ячейки и выделить нужный диапазон A2:A8)
Ø Значения X – диапазон, содержащий данные факторов независимого признака (аналогично B2:B8)
|
|
|
Ø Константа=1
Ø Статистика=1 (см.рис.3)

Рис.3. Окно аргументов функции “Линейн”
7) В левой верхней ячейке появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу нажмите F2, а затем комбинацию клавиш <CTRL>+<SHIFT>+<ENTER>.
Дополнительная регрессионная статистика выводится в следующем порядке
| Значение коэффициента b | Значение коэффициента a |
| Среднеквадратическое отклонение b | Среднеквадратическое отклонение a |
| Коэффициент детерминации R2 | Среднеквадратическое отклонение y |
| F-статистика | Число степеней свободы |
| Регрессионная сумма квадратов | Остаточная сумма квадратов |

Рис.4. Результаты построения линейной модели
В соответствии с полученными результатами можно записать уравнение линейной регрессии:
y=18,8683+0,79693*x
II. Для вычисления параметров экспоненциальной кривой y=α*βx воспользуйтесь встроенной статистической функцией ЛГРФПРИБЛ. Порядок вычислений аналогичен применению предыдущей функции. Результаты показаны на рис.5

Рис.5. Результаты построения экспоненциальной модели
В соответствии с полученными результатами можно записать уравнение:
y=27,03135* 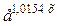
III.  Для построения гиперболической функции воспользуйтесь функцией ЛИНЕЙН, взяв в качестве факторного признака величину 1/X. Для этого в столбце С в ячейке С1 записать название столбца “1/X”, а в ячейку С2 ввести формулу =1/B2, после чего, выделив ячейку С2, навести курсор мыши в правый нижний угол ячейки (появится крестик) нажать левую кнопку и, не отпуская, растянуть выделенную ячейку мышкой до ячейки С8 включительно. Затем воспользоваться уже известной функцией Линейн, взяв в качестве параметра Известные_значения_x диапазон С2:С8. Результаты представлены на рис. 6.
Для построения гиперболической функции воспользуйтесь функцией ЛИНЕЙН, взяв в качестве факторного признака величину 1/X. Для этого в столбце С в ячейке С1 записать название столбца “1/X”, а в ячейку С2 ввести формулу =1/B2, после чего, выделив ячейку С2, навести курсор мыши в правый нижний угол ячейки (появится крестик) нажать левую кнопку и, не отпуская, растянуть выделенную ячейку мышкой до ячейки С8 включительно. Затем воспользоваться уже известной функцией Линейн, взяв в качестве параметра Известные_значения_x диапазон С2:С8. Результаты представлены на рис. 6.

Рис.6. Результат построения гиперболической функции
Запишем уравнение гиперболической функции:
y=84,31121-1228,79/x
IV. Отразите полученные результаты расчетов на графике.
Для этого выполните следующую последовательность действий:
1. Выберите в меню Вставка->Диаграмма, Тип-Точечная. ( рисунок 7)
|
|
|

Рис.7 Выбор типа диаграммы
2. Введите диапазон входных данных (рисунок 8)

Рис.8. Выбор источника данных для диаграммы
3. Оформите вид полученного графика (подписи осей, название графика, и т.д.)
4. Выберите место отображения графика (в имеющемся).
5. Добавьте линию тренда:
- выделите полученную диаграмму и выберите на панели управления
Диаграмма->Добавить линию тренда;
- выбираем Тип-Линейная;
- в закладке Параметры ставим галочки:
 Показывать уравнение на диаграмме
Показывать уравнение на диаграмме
 Поместить на диаграмме величину достоверности аппроксимации (R^2).
Поместить на диаграмме величину достоверности аппроксимации (R^2).
Полученная диаграмма представлена на рисунке 9.

Рис.9. Графическое представление линейной модели
V. Осуществляя аналогичные действия, но, указав в Параметрах линии тренда Тип-Экспоненциальная, получим графическое представление экспоненциальной модели (рисунок 10).

Рис.10. Графическое представление экспоненциальной модели
VI. Для гиперболической модели порядок действий аналогичен построению линейной модели, но входной диапазон для X-столбца необходимо указать со значениями 1/X (С2:С8).

Рис.11. Графическое представление гиперболической модели
VII. Сравним по качеству полученные модели. Для этого результаты вычислений представим в сводной таблице.
Таблица 1
Сводная таблица результатов вычислений
| Модель Показатель | Линейная | Экспоненциальная | Гиперболическая |
| Коэффициент детерминации R2 | 0,971217 | 0,958292 | 0,929001 |
| Значение F-критерия Фишера | 168,714 | 114,8816 | 65,42338 |
Вывод: Лучшей по качеству моделью признается модель, обладающая большим значением коэффициента детерминации. Коэффициент детерминации R2 показывает долю вариации результативного признака под воздействием факторных признаков, введенных в модель регрессии.
Для линейной модели 97,12 % вариации объема выпуска продукции определяется вариацией объема капиталовложений, что является максимальным значением коэффициента детерминации из всех 3-х моделей. Следовательно, в качестве лучшей модели следует выбрать линейную модель.
Проверка статистической значимости уравнения регрессии осуществляется по F-критерию Фишера, для этого находим FТабл.= 5,987378 с помощью функции FPACПОБР (для a = 0,05, k1 = 1, k2 = 6). FТабл.<FРасч. для каждой из моделей, следовательно, полученные уравнения регрессий следует признать адекватными, а модели значимыми, при этом лучшей моделью по значению коэффициента детерминации признается модель линейной регрессии.
Задания для самостоятельной работы к задаче 1
| Вариант | Признаки | Наблюдения | ||||||
| Y | ||||||||
| X | ||||||||
| Y | ||||||||
| X | ||||||||
| Y | ||||||||
| X | ||||||||
| Y | ||||||||
| X | ||||||||
| Y | ||||||||
| X | ||||||||
| Y | ||||||||
| X | ||||||||
| Y | ||||||||
| X | ||||||||
| Y | ||||||||
| X | ||||||||
| Y | ||||||||
| X | ||||||||
| Y | ||||||||
| X | ||||||||
Задача 2
|
|
|
Аналитический отдел предприятия осуществляет анализ зависимости прибыли предприятия (Y, млн.руб.) от величины оборотного капитала (X1, млн.руб.) и стоимости основных средств (X2, млн.руб).
| Y | ||||||||||
| X1 | ||||||||||
| X2 |
Требуется:
1. Вычислить статистические характеристики для каждого показателя.
2. Построить матрицу коэффициентов парной корреляции и осуществить её анализ. Обосновать выбор факторных признаков.
3. Построить однофакторную линейную регрессию, рассчитать её параметры. Проанализировать значение коэффициента регрессии.
4. Вычислить точечный прогноз факторного признака, построив по нему линейный тренд.
5. Определить прогнозные значения результативного признака.
6. Результаты расчетов отразить на графике.
Решение
I. Сводную таблицу основных статистических характеристик для одного или нескольких массивов данных можно получить с помощью инструмента анализа данных Описательная статистика. Для этого выполните следующие шаги:
1. Введите исходные данные в MS Excel.
2. В главном меню выберите Сервис->Анализ данных->Описательная статистика (если в закладке Сервис пункт Анализ данных отсутствует, то выберите Сервис-Надстройки и поставьте галочку напротив Пакет анализа) (рисунок 12)

Рис.12. Выбор надстройки “Пакет анализа”
3. Заполните диалоговое окно ввода параметров:
· Входной интервал – диапазон, содержащий анализируемые данные (3 столбца в нашем случае).
· Группирование – по столбцам.
· Метки - флажок, который указывает, содержит ли первая строка названия столбцов или нет (в нашем случае - содержит).
· Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона.
· Итоговая статистика – поставить галочку.
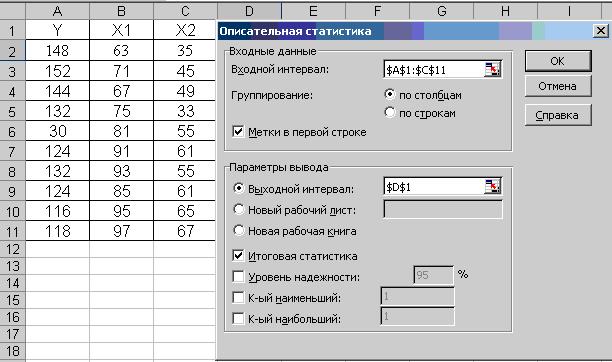
Рис.13. Параметры инструмента «Описательная статистика»
Результаты вычислений представлены на рисунке 14.

Рис.14. Описательная статистика
II. Матрицу парных коэффициентов корреляции можно рассчитать, используя инструмент Анализа данных Корреляция. Для этого:
1. В главном меню выбрать Сервис->Анализ данных->Корреляция
2. Заполнить диалоговое окно ввода параметров, в качестве входного интервала следует указать весь диапазон представленных данных (рисунок 15).

Рис.15. Параметры инструмента «Корреляция»
3. Результаты построения матрицы коэффициентов парной корреляции представлены на рисунке 16.

Рис.16. Матрица коэффициентов парной корреляции
Коэффициент парной корреляции между прибылью предприятия и величиной оборотного капитала  имеет отрицательную величину, следовательно, между этими признаками имеет место обратная связь, т.е. при увеличении величины оборотного капитала прибыль предприятия уменьшается. Значение коэффициента невелико по абсолютной величине, следовательно, между прибылью предприятия и величиной оборотного капитала имеет место слабая связь. Эта тенденция имеет негативный характер и в качестве рекомендаций предприятию следует предложить осуществление детального анализа всех направлений использования оборотного капитала.
имеет отрицательную величину, следовательно, между этими признаками имеет место обратная связь, т.е. при увеличении величины оборотного капитала прибыль предприятия уменьшается. Значение коэффициента невелико по абсолютной величине, следовательно, между прибылью предприятия и величиной оборотного капитала имеет место слабая связь. Эта тенденция имеет негативный характер и в качестве рекомендаций предприятию следует предложить осуществление детального анализа всех направлений использования оборотного капитала.
Коэффициент парной корреляции между прибылью предприятия и стоимостью основных средств  также имеет отрицательную величину, следовательно, между этими признаками имеет место обратная связь, что также свидетельствует о необходимости анализа всех направлений финансово-хозяйственной политики предприятия.
также имеет отрицательную величину, следовательно, между этими признаками имеет место обратная связь, что также свидетельствует о необходимости анализа всех направлений финансово-хозяйственной политики предприятия.
Из матрицы парных коэффициентов корреляции видно, что между величиной оборотного капитала и стоимостью основных средств (факторами X1 и X2) существует эффект мультиколлинеарности (коэффициент корреляции между ними  >0,8), следовательно, оба фактора одновременно в модель регрессии включать нельзя, один из факторов необходимо из рассмотрения исключить. Из рассмотрения исключается тот фактор, который оказывает меньшее влияние на прибыль предприятия (результативный признак).
>0,8), следовательно, оба фактора одновременно в модель регрессии включать нельзя, один из факторов необходимо из рассмотрения исключить. Из рассмотрения исключается тот фактор, который оказывает меньшее влияние на прибыль предприятия (результативный признак).
В данной задаче из рассмотрения необходимо исключить X1, так он оказывает меньшее влияние на результативный признак (коэффициент парной корреляции между Х1 и Y меньше по модулю, чем между X2 и Y), т.е.
 .
.
Итак, по результатам анализа матрицы парных коэффициентов корреляции в качестве факторного признака для построения однофакторной регрессии должен быть выбран фактор Х2 (стоимость основных средств).
III. С помощью инструмента анализа данных Регрессия, помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов, можно получить остатки и графики подбора линии регрессии, остатков и нормальной вероятности. Порядок действий следующий:
1. Для построения модели парной регрессии в главном меню выберите Сервис->Анализ данных->Регрессия
2. Заполните диалоговое окно ввода данных и параметров вывода (рисунок 17)
· Входной интервал Y – диапазон, содержащий данные результативного признака.
· Входной интервал X – диапазон, содержащий данные факторов независимого признака (так как модель однофакторная, то построим её на основе фактора X2)
· Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет.
· Константа-ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении (метку напротив параметра не ставить).
· Выходной интервал – достаточно указать левую верхнюю ячейку диапазона с выходными данными регрессионного анализа.
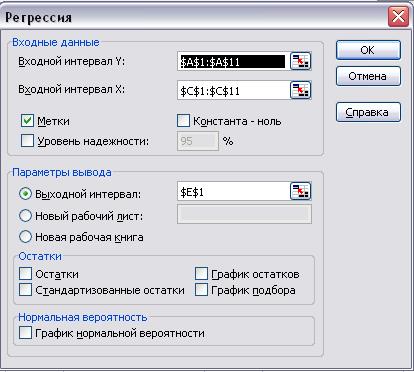
Рис.17. Параметры инструмента «Регрессия»
Результаты регрессионного анализа представлены на рисунке 18.

Рис.18. Результаты регрессионного анализа
На основании этого можно записать уравнение линейной парной регрессии:
y = 173.678 - 0.98248 * x
При увеличении стоимости основных средств (Х2) на 1 млн.руб. прибыль предприятия (y) уменьшается на 0,98248 млн.рублей, что свидетельствует о нерациональном использовании финансовых ресурсов предприятия и необходимости пересмотра направлений финансово-хозяйственной политики предприятия.
IV. Для определения точечного прогноза факторного признака (X2), необходимо воспользоваться мастером диаграмм, в качестве параметра взяв диапазон для X2 – C2:С11 (рисунок 19).

Рис.19. Выбор типа диаграммы
На полученном графике необходимо добавить линию тренда (эта процедура подробно рассмотрена в задаче 1).

Рис.20. Построение линейного тренда по факторному признаку Х2
Исходя из полученного уравнения тренда, можно рассчитать прогнозное значение фактора X2 (для следующего, 11-го, момента времени):
X2 =3,3939*11+33,933=71,2659 (млн.руб.)
Прогнозное значение стоимости основных средств (Х2) может быть отображено на рис.20).
V. Для получения прогнозного значения прибыли предприятия (результативного признака) необходимо в уравнение однофакторной регрессии подставить полученное значение прогноза стоимости основных средств (факторного признака):
y = 173.678 – 0.98248 * 71.2659 = 103.66068 (млн.руб.)
VI. Для отображения прогнозного значения результативного признака нужно воспользоваться мастером диаграмм (рисунок 21)
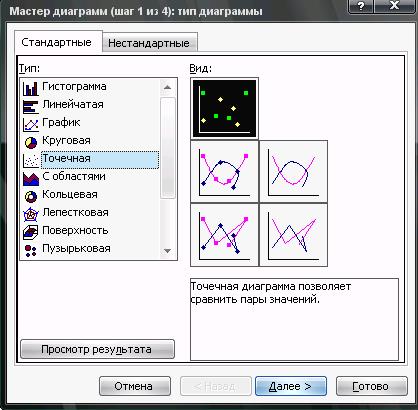
Рис.21 Выбор типа диаграммы
В качестве входных диапазонов необходимо взять данные для факторного признака X2 - (C2:C11), для результативного признака Y - (A2:A11), на полученном графике отразить линию тренда (рисунок 22).
Для отображения на графике прогноза прибыли предприятия (Y) необходимо:
· Выделить полученный график
· Щелкнуть на нем правой кнопкой мыши и выбрать Исходные данные
· Добавить новый ряд, и ввести прогнозные значения X и Y, рассчитанные ранее.

Рис.22. Добавление на график прогнозного значения прибыли предприятия
Окончательный вид графика будет следующий (рисунок 23).
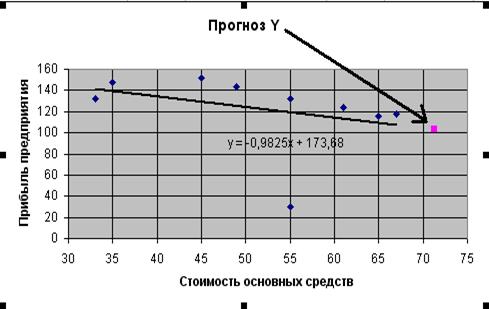
Рис.23. Построение прогноза прибыли предприятия (Y)
Задания для самостоятельной работы к задаче 2
| Вариант | Признак | Наблюдения | |||||||||
| Y | |||||||||||
| X1 | |||||||||||
| X2 | |||||||||||
| Y | |||||||||||
| X1 | |||||||||||
| X2 | |||||||||||
| Y | |||||||||||
| X1 | |||||||||||
| X2 | |||||||||||
| Y | |||||||||||
| X1 | |||||||||||
| X2 | |||||||||||
| Y | |||||||||||
| X1 | |||||||||||
| X2 | |||||||||||
| Y | |||||||||||
| X1 | |||||||||||
| X2 | |||||||||||
| Y | |||||||||||
| X1 | |||||||||||
| X2 | |||||||||||
| Y | |||||||||||
| X1 | |||||||||||
| X2 | |||||||||||
| Y | |||||||||||
| X1 | |||||||||||
| X2 | |||||||||||
| Y | |||||||||||
| X1 | |||||||||||
| X2 |
Задача 3
По десяти кредитным учреждениям получены данные, характеризующие зависимость объема прибыли (Y, млн.руб.) от величины доходов по кредитам (X1, млн.руб.), доходов по депозитам (X2, млн.руб.) и размера внутрибанковских расходов (X3, млн.руб.).
| Y | ||||||||||
| X1 | ||||||||||
| X2 | ||||||||||
| X3 |
Требуется:
1. Осуществить выбор факторных признаков для построения многофакторной регрессионной модели.
2. Рассчитать параметры регрессионной модели. Оценить ее качество.
3. Для характеристики модели определить:
· средние коэффициенты эластичности;
· бета-коэффициенты,
· дельта-коэффициенты.
4. Оценить с помощью t-критерия Стьюдента статистическую значимость коэффициентов уравнения множественной регрессии.
5. Построить регрессионную модель со статистически значимыми факторами. Оценить ее качество.
6. Определить точечный и интервальный прогноз результативного показателя.
Решение
I. Выбор факторных признаков для построения модели осуществляется с помощью матрицы коэффициентов парной корреляции. Для её построения необходимо:
· выбрать Сервис->Анализ данных->Корреляция
· заполнить необходимые поля диалогового меню (рисунок 24)

Рис.24. Ввод параметров инструмента «Корреляция»
Результаты представлены на рисунке 25.

Рис.25. Таблица коэффициентов парных корреляций
Для выявления явления мультиколлинеарности необходимо проанализировать коэффициенты парной корреляции между факторными признаками. Если имеют место коэффициенты, значение которых по модулю больше 0,8, то, следовательно, мультиколлинеарность присутствует, и это явление необходимо устранять. Если же значения коэффициентов парной корреляции между факторными признаками, взятые по модулю, меньше величины 0,8, то явление мультиколлинеарности отсутствует, и, следовательно, все факторные признаки можно включать в модель множественной регрессии.
Так как  , т.е. между факторными признаками X1 и X3 существует явление мультиколлинеарности, то для построения модели выбираем тот факторный признак, который оказывает большее влияние на результативный признак (фактор, для которого коэффициент парной корреляции с результативным признаком, взятый по модулю, является большим).
, т.е. между факторными признаками X1 и X3 существует явление мультиколлинеарности, то для построения модели выбираем тот факторный признак, который оказывает большее влияние на результативный признак (фактор, для которого коэффициент парной корреляции с результативным признаком, взятый по модулю, является большим).

Следовательно, фактор X3 оказывает большее влияние на результативный признак (Y) и этот фактор рекомендуется в модели оставить. Фактор X1 оказывает меньшее влияние на результативный признак (Y) и этот фактор рекомендуется из модели исключить.
Таким образом, для построения модели множественной регрессии выбираются два факторных признака - Х2 (величина доходов по депозитам) и Х3 (величина внутрибанковских расходов).
II. Расчет параметров регрессионной модели можно осуществить с помощью инструмента анализа данных Регрессия (см. задача 2), отличие заключается в том, что в качестве диапазона значений фактора X необходимо указать диапазон значений факторов X2 и X3 (рисунок 26).

Рис.26. Ввод параметров регрессии
Результаты построение множественной регрессии представлены на рисунке 27.

Рис.27. Вывод итогов регрессии
На основании полученных данных можно записать уравнение множественной регрессии
Y=-16,2872 + 0,197247*X2 + 0,592429*X3
Оценим качество построенной модели множественной регрессии по следующим направлениям:
· Коэффициент детерминации  = 0.794176 достаточно близок к 1, следовательно, качество модели можно признать высоким.
= 0.794176 достаточно близок к 1, следовательно, качество модели можно признать высоким.
· Критерий Фишера F = 13,50486 > Fтабл = 4,74, следовательно, уравнение регрессии признается статистически значимым и может быть использовано для анализа и прогнозирования экономических процессов.
Для вычисления Fтабл необходимо определить:
- степень свободы числителя m=2 (число факторных признаков);
- степень свободы знаменателя n-m-1=10-2-1=7;
- уровень значимости  =0,05.
=0,05.
III. Оценим качество построенной модели множественной регрессии с помощью коэффициентов эластичности, b - и D - коэффициентов.
Коэффициент эластичности определяется:
 , (1)
, (1)
где 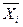 - среднее значение соответствующего факторного признака,
- среднее значение соответствующего факторного признака,
 - среднее значение результативного признака.
- среднее значение результативного признака.
bi – коэффициенты регрессии соответствующих факторных признаков.
ß-коэффициент определяется по следующей формуле:
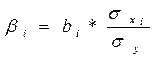 , (2)
, (2)
где 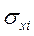 - среднеквадратическое отклонение (СКО) соответствующего факторного признака (рассчитывается как корень квадратный из дисперсии признака),
- среднеквадратическое отклонение (СКО) соответствующего факторного признака (рассчитывается как корень квадратный из дисперсии признака),
 - СКО результативного признака.
- СКО результативного признака.
∆-коэффициент определяется по следующей формуле:
 , (3)
, (3)
где  - коэффициент парной корреляции результативного и соответствующего факторного признаков,
- коэффициент парной корреляции результативного и соответствующего факторного признаков,
 - коэффициент детерминации.
- коэффициент детерминации.
На рисунке 28 представлены формулы расчетов описанных выше коэффициентов

Рис.28. Формулы расчетов коэффициентов
Результаты вычислений представлены в таблице 2.
Таблица 2
Результаты расчета бета-, дельта- и коэффициентов эластичности
| Y | X2 | X3 |
|
|
|


