 |
О функции Грина разнопорядковой краевой задачи.
|
|
|
|
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
“ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ”
Факультет математический
Кафедра функционального анализа
<Тема выпускной квалификационной работы>
ВКР <указать вид в соответствии с ГОC>
<Шифр, наименование направления подготовки / специальности>
<Наименование специализации>
Допущено к защите в ГАК
Зав. кафедрой < Подпись> <расшифровка> <ученая степень, звание> __.__.200__
Студент < Подпись> <расшифровка подписи>
Руководитель < Подпись> <расшифровка подписи> <ученая степень, звание>
Консультант < Подпись> <расшифровка подписи> <ученая степень, звание>
Воронеж200 9
О ФУНКЦИИ ГРИНА РАЗНОПОРЯДКОВОЙ КРАЕВОЙ ЗАДАЧИ.
Для струнно-стержневой модели
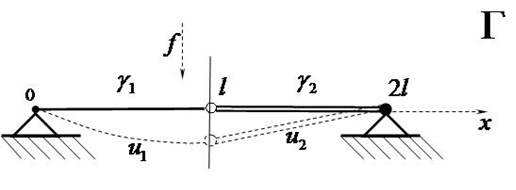 |
рассмотрим краевую задачу:
 , (1)
, (1)
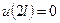 , (2)
, (2)
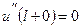 , (3)
, (3)
 , (4)
, (4)
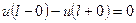 , (5)
, (5)
 , (6)
, (6)
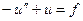 на
на 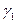 , (7)
, (7)
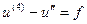 на
на 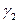 . (8)
. (8)
По левым частям равенств (1) – (6) построим функционалы  , а левым частям равенств (7), (8) – дифференциальный оператор
, а левым частям равенств (7), (8) – дифференциальный оператор 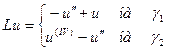 .
.
Тогда задачу (1) – (8) можно записать в виде:

Если задача (9), (10) невырожденна (т.е. имеет единственное решение) на 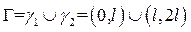 , то ее решение для функций
, то ее решение для функций 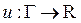 таких, что
таких, что 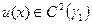 ,
, 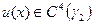 , и любой
, и любой 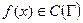 может быть представлено в виде
может быть представлено в виде
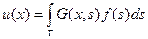 . (11)
. (11)
Функцию 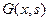 , для которой (11) справедливо, назовем функцией Грина задачи (9), (10).
, для которой (11) справедливо, назовем функцией Грина задачи (9), (10).
Наша задача и состояла в отыскании (построении) такой функции.
Определение. Функцией Грина 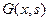 на отрезке называют функцию двух переменных
на отрезке называют функцию двух переменных 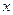 и
и  , при каждом фиксированном
, при каждом фиксированном  из отрезка, обладающую свойствами:
из отрезка, обладающую свойствами:
1. при 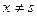
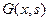 удовлетворяет по
удовлетворяет по 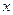 однородному дифференциальному уравнению;
однородному дифференциальному уравнению;
2. при 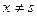
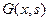 удовлетворяет по
удовлетворяет по 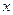 краевым условиям;
краевым условиям;
3. при 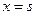 непрерывна по
непрерывна по 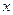 , т.е.
, т.е.
|
|
|
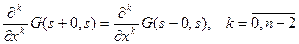 ,
,
(для уравнения порядка 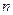 )
)
4. при 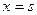 имеет скачек, т.е.
имеет скачек, т.е.
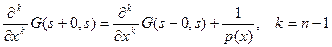 ,
,
(где 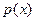 - коэффициент при старшей производной дифференциального уравнения порядка
- коэффициент при старшей производной дифференциального уравнения порядка 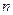 ).
).
Функцию Грина задачи (9), (10) на графе  можно построить по формуле:
можно построить по формуле:
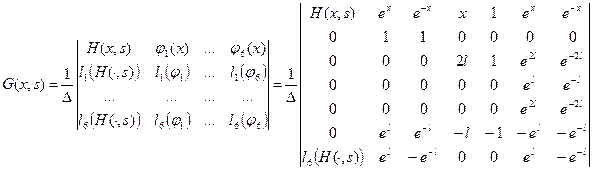 (12’)
(12’)
где  - фундаментальная система решений однородного уравнения
- фундаментальная система решений однородного уравнения 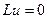 ,
,
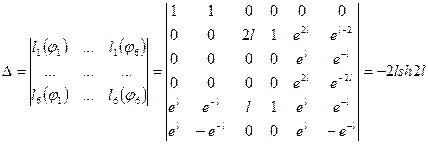 , (13)
, (13)
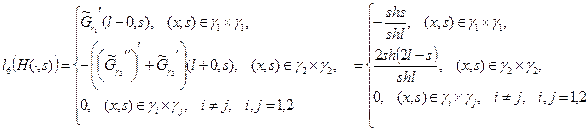
Функцию  можно построить по функциям Грина двухточечных задач (задач на отрезках) на
можно построить по функциям Грина двухточечных задач (задач на отрезках) на  и
и  :
:
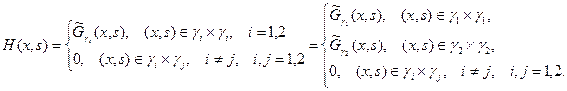 (14)
(14)
где 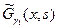 - функция Грина двухточечной краевой задачи на отрезке
- функция Грина двухточечной краевой задачи на отрезке 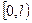 :
:
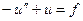 на
на 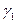 ,
,
 , (15)
, (15)
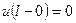 ,
,
а 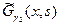 - функция Грина двухточечной краевой задачи на
- функция Грина двухточечной краевой задачи на  :
:
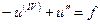 на
на 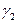 ,
,
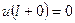 ,
,
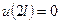 , (16)
, (16)
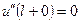 ,
,
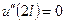 .
.
Найдем сначала функцию Грина задачи (15).
Согласно определению функции Грина на отрезке, она должна удовлетворять однородному уравнению, поэтому найдем фундаментальную систему решений однородного уравнения 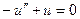 :
: 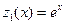 ,
, 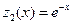 .
.
По левым частям краевых условий (15) построим функционалы: 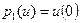 ,
, 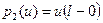 .
.
Так как функция Грина должна удовлетворять краевым условиям, то
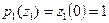 ,
, 
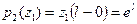 ,
, 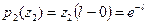 . (17)
. (17)
Функцию Грина задачи (15) будем искать в виде:
 ,
,
где по равенствам (17) можно найти 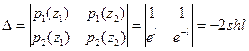 ,
,
функция 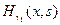 - какое-либо решение неоднородного уравнения задачи (15), которое может быть найдено, например, с помощью функции Коши:
- какое-либо решение неоднородного уравнения задачи (15), которое может быть найдено, например, с помощью функции Коши:
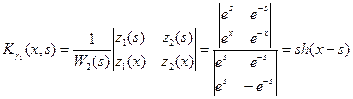 .
.
Итак
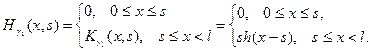
И, следовательно,

Найдем теперь функцию Грина задачи (16).
Найдем фундаментальную систему решений однородного уравнения 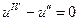 :
: 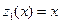 ,
, 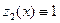
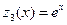
 .
.
По левым частям краевых условий задачи (16) построим функционалы:
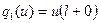 ,
,
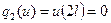 ,
,
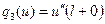 ,
,
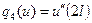 .
.
Функцию Грина задачи (16) будем искать в виде:
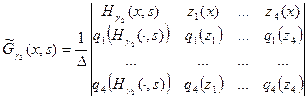 ,
,
где 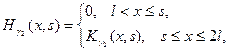
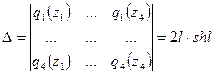 .
.
Функция 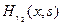 - решение неоднородного уравнения задачи (16), которое найдем с помощью функции Коши:
- решение неоднородного уравнения задачи (16), которое найдем с помощью функции Коши:
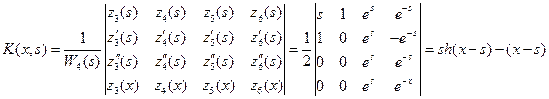 .
.
Найдем
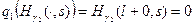 ,
,
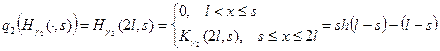 ,
,
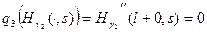 ,
,
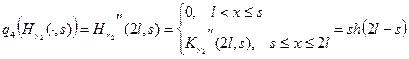 ,
,
тогда

В силу построения функции Грина задачи (9), (10) было установлено, что  , что эквивалентно условию невырожденности (единственности) задачи (9), (10).
, что эквивалентно условию невырожденности (единственности) задачи (9), (10).
Рассмотрим теперь задачу
 , (1)
, (1)
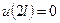 , (2)
, (2)
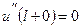 , (3)
, (3)
 , (4)
, (4)
|
|
|
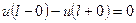 , (5)
, (5)
 , (6)
, (6)
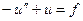 на
на 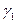 , (7)
, (7)
 на
на 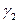 . (8’)
. (8’)
где в уравнении (8) в старшей производной стоит параметр  .
.
Также как и раньше строим функционалы  , а левым частям равенства (7), (8’) – дифференциальный оператор:
, а левым частям равенства (7), (8’) – дифференциальный оператор:
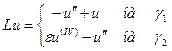
Тогда задачу (1) – (7), (8’) можно записать в виде:

Функцию Грина задачи (9’), (10’) на графе  можно построить по формуле:
можно построить по формуле:
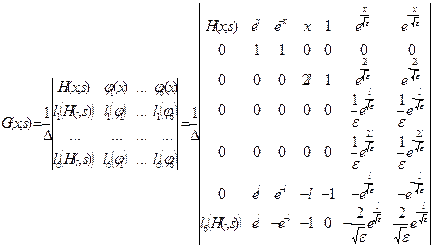 (12’)
(12’)
где 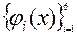 - фундаментальная система решений однородного уравнения
- фундаментальная система решений однородного уравнения
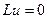 ,
,
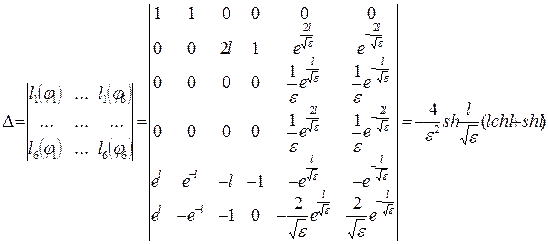
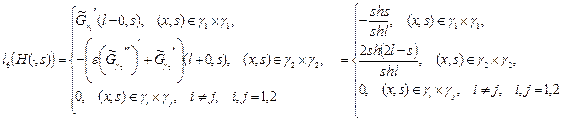 (13’)
(13’)
Функцию  можно построить по функциям Грина двухточечных задач (задач на отрезках) на
можно построить по функциям Грина двухточечных задач (задач на отрезках) на  и
и 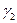 :
:
 (14')
(14')
где 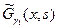 - функция Грина двухточечной краевой задачи на отрезке
- функция Грина двухточечной краевой задачи на отрезке 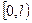 :
:
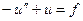 на
на 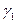 ,
,
 , (15)
, (15)
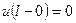 ,
,
а 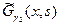 - функция Грина двухточечной краевой задачи на
- функция Грина двухточечной краевой задачи на 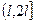 :
:
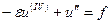 на
на 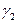 ,
,
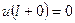 ,
,
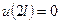 , (16’)
, (16’)
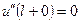 ,
,
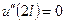 .
.
Функция Грина задачи (15) была рассмотрена ранее.
Найдем функцию Грина задачи (16’)
Найдем фундаментальную систему решений однородного уравнения 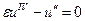 :
:  ,
, 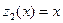
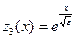
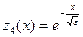 .
.
По левым частям краевых условий задачи (16’) построим функционалы:
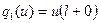 ,
,
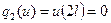 ,
,
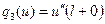 ,
,
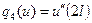 .
.
Функцию Грина задачи (16’) будем искать в виде:
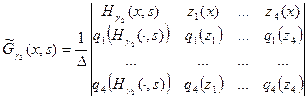 ,
,
где 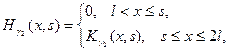
 .
.
Функция 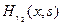 - решение неоднородного уравнения задачи (16’), которое найдем с помощью функции Коши:
- решение неоднородного уравнения задачи (16’), которое найдем с помощью функции Коши:
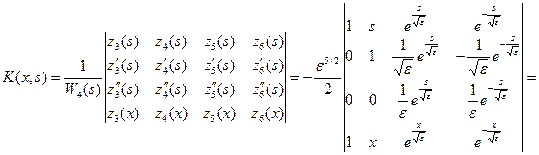
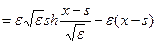
Найдем
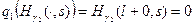 ,
,
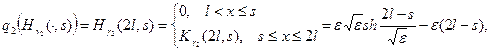
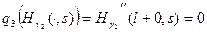 ,
,
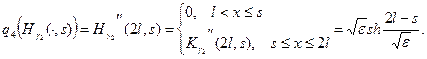
тогда
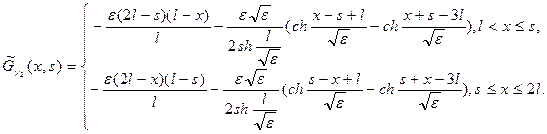
Найдем из 12’

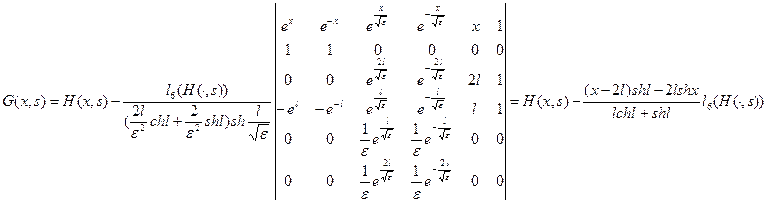
Учитывая (13’) и (14’), получаем

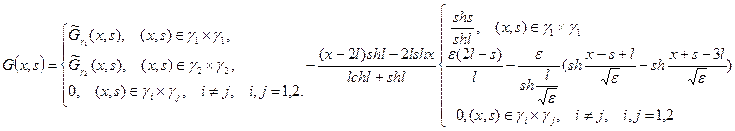
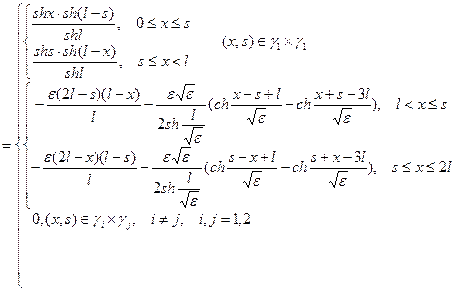 -
-
-  =
=
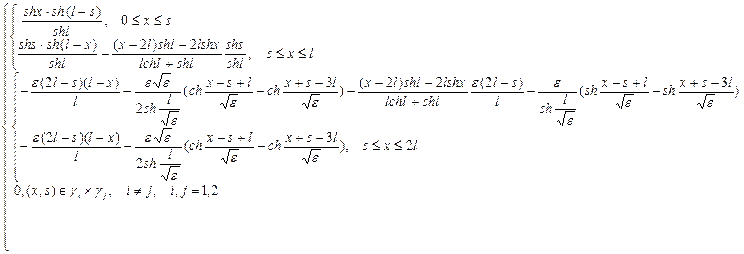
Рассмотрим краевую задачу:
 , (1)
, (1)
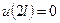 , (2)
, (2)
 , (3)
, (3)
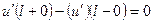 , (4)
, (4)
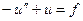 на
на 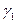 , (5)
, (5)
 на
на 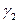 . (6)
. (6)
По левым частям равенств (1) – (4) построим функционалы 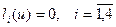 , а левым частям равенств (5), (6) – дифференциальный оператор
, а левым частям равенств (5), (6) – дифференциальный оператор  .
.
Тогда задачу (1) – (8) можно записать в виде:

Если задача (9), (10) невырожденна (т.е. имеет единственное решение) на 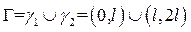 , то ее решение для функций
, то ее решение для функций 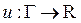 таких, что
таких, что 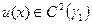 ,
, 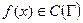 может быть представлено в виде
может быть представлено в виде
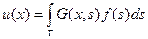 . (9)
. (9)
Функцию 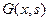 , для которой (9) справедливо, назовем функцией Грина задачи (7), (8).
, для которой (9) справедливо, назовем функцией Грина задачи (7), (8).
Функцию Грина задачи (7), (8) на графе  будем искать в виде:
будем искать в виде:
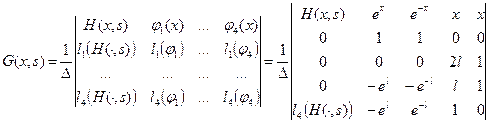 (10)
(10)
где  - фундаментальная система решений однородного уравнения
- фундаментальная система решений однородного уравнения 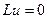 ,
,
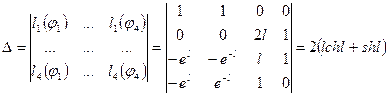 , (12)
, (12)
 (13)
(13)
Функцию  можно построить по функциям Грина двухточечных задач (задач на отрезках) на
можно построить по функциям Грина двухточечных задач (задач на отрезках) на  и
и 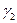 :
:
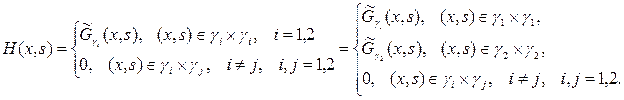 (14)
(14)
где 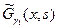 - функция Грина двухточечной краевой задачи на отрезке
- функция Грина двухточечной краевой задачи на отрезке 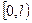 :
:
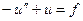 на
на 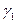 ,
,
 , (15)
, (15)
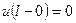 ,
,
а 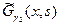 - функция Грина двухточечной краевой задачи на
- функция Грина двухточечной краевой задачи на 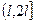 :
:
 на
на 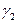 ,
,
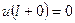 ,
,
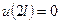 . (16)
. (16)
Найдем сначала функцию Грина задачи (15).
|
|
|
Согласно определению функции Грина на отрезке, она должна удовлетворять однородному уравнению, поэтому найдем фундаментальную систему решений однородного уравнения 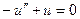 :
: 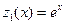 ,
, 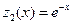 .
.
По левым частям краевых условий (16) построим функционалы: 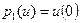 ,
, 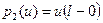 .
.
Так как функция Грина должна удовлетворять краевым условиям, то
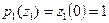 ,
, 
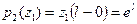 ,
, 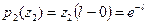 . (17)
. (17)
Функцию Грина задачи (15) будем искать в виде:
 ,
,
где по равенствам (16) можно найти 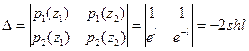 ,
,
функция 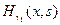 - какое-либо решение неоднородного уравнения задачи (16), которое может быть найдено, например, с помощью функции Коши:
- какое-либо решение неоднородного уравнения задачи (16), которое может быть найдено, например, с помощью функции Коши:
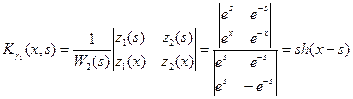 .
.
Итак
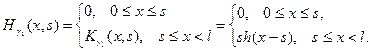
И, следовательно,
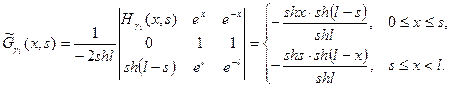
или
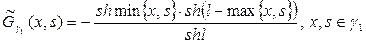
Найдем теперь функцию Грина задачи (16).
Найдем фундаментальную систему решений однородного уравнения 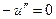 :
: 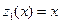 ,
, 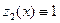 .
.
По левым частям краевых условий задачи (16) построим функционалы:
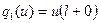 ,
,
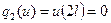 .
.
Функцию Грина задачи (16) будем искать в виде:
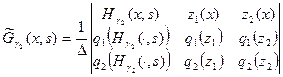 ,
,
где 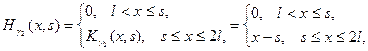
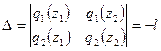 .
.
Функция  - решение неоднородного уравнения задачи (16), которое найдем с помощью функции Коши:
- решение неоднородного уравнения задачи (16), которое найдем с помощью функции Коши:
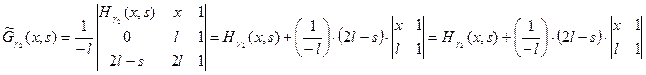
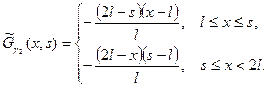 .
.
Или
 .
.
Найдем
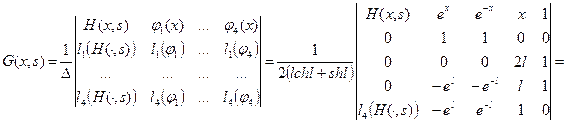
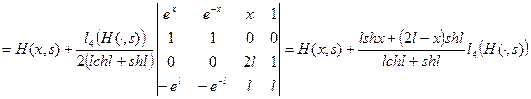 .
.
Учитывая (13) и (14), имеем
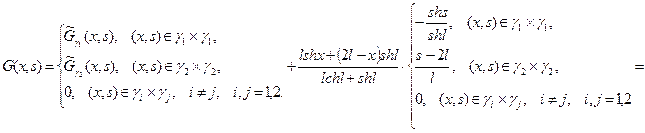
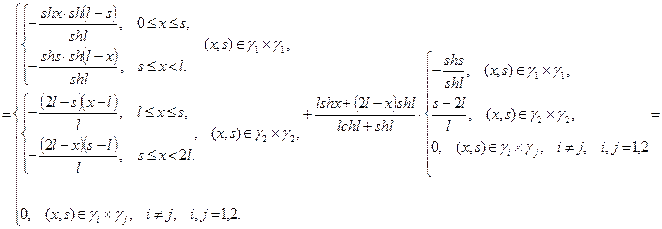
Тогда
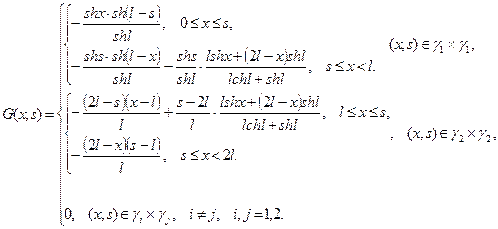
ЛИТЕРАТУРА
1. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление Серия: «Курс высшей математики и математической физики» -3выпуск/Главная редакция физико-математической литературы. - М.:Наука,1969.-424с.
2. Камке Э. Справочник по обыкновенным дифференциальным уравнениям. – М.: Физматлит, 1961.
3. Наймарк М.А. Линейные дифференциальные операторы. – М.: Наука, 1969.
4. Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений/ Под ред. И.Е. Морозова – М.:Наука, 1964.- 272с.
5. Покорный Ю.В. Дифференциальные уравнения на геометрических графах/Ю.В. Покорный, О.М. Пенкин, В.Л. Прядиев, А.В. Боровских. К.П. Лазарев, С.А. Шабров -М.: Физматлит, 2004.- 272с.
6. Белоглазова Т.В. О положительной обратимости разнопорядковых задач на графах/ кандидатская диссертация – Воронеж, 2003. – 128 с.
|
|
|


