 |
Сравнение выборок. Часть 2.
|
|
|
|
Лабораторная работа №5
Сравним 5-ти и 35-ти дневных щенков песцов по активности фермента каталазы в сердце:
5 дневные: 41, 44, 31, 38, 43, 29, 71, 45;
35 дневные: 52, 51, 62, 52, 52, 50, 54, 62, 31;
Для начала проверьте, все ли варианты принадлежат выборке, подсчитайте средние арифметические, стандартные отклонения, дисперсии, коэффициенты вариации. Проверьте их достоверность. Отличается ли активность фермента?
Задание 1. Проверьте достоверность отличия по критерию Стьюдента.
Задание 2. Проверьте достоверность отличия по критерию Уилкоксона-Манна-Уитни. Этот метод сравнения двух выборок признается наиболее чувствительным, мощным и в то же время достаточно простым для расчетов. Согласно нулевой гипотезе, сравниваемые совокупности имеют одинаковые распределения. Техника метода:
- все варианты сравниваемых выборок ранжируют в одном общем ряду:
- каждому значению присваивают ранг, (порядковый номер). При этом одинаковым (повторяющимся) значениям вариант должен соответствовать один и тот же средний ранг (суммируют порядковые номера всех равнозначных вариант и делят на число слагаемых).
- после этого ранги вариант суммируют отдельно по каждой выборке:
R1= ∑xi R2- ∑xn
- затем вычисляют величину критерия Уилкоксона (V):
U – 0.5n1n2
V = ----------------------------------, где
√(n1n2(n+1)/ 12)
U= максимальное значение из двух величин U1 или U2
n – объём выборки с максимальным значением U
U1= n1n2 + 0.5n1 (n1+1)-R1
U2= n1n2 + 0.5n2 (n2+1)-R2
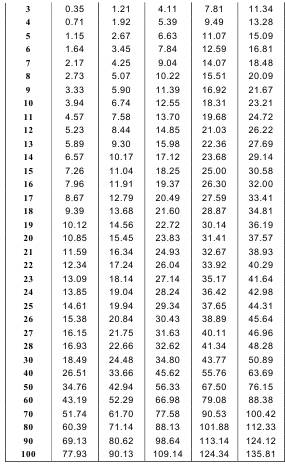
- Если выборка достаточно велика (n>20), величина статистики V сравнивается с табличным значением критерия Стьюдента (Т) для df = ∞ и α = 0.1 (т. е. только для верхней 95% области нормального распределения). Считается, что метод хорошо работает для выборок объемом больше 10. В случае с меньшими выборками нужно пользоваться таблицами Уилкоксона – Манна – Уитни (табл. 11П), где сравниваются.Umax и Uтабл. (если Umax > Uтабл, то Н0 отвергается).
|
|
|
Задание 3. Проверьте достоверность отличия по критерию Уайда (Т). Техника расчетов аналогична; результатом первого этапа обработки должны стать два значения суммы рангов по выборкам, из которых выбирается меньшее значение: T = min(R1, R2). Достоверность отличий выборок оценивается с помощью критерия Т Уайта по специальной таблице 12П. Полученная величина сравнивается с табличным значением критерия с учетом объема сравниваемых совокупностей для принятой доверительной вероятности: Р = 0.95 или Р = 0.99 (т. е. для уровня значимости α = 0.05 и α = 0.01). Если расчетное значение Т меньше табличного числа (ТЭ < ТT), это указывает на достоверность отличий между выборками, и нулевая гипотеза (о том, что распределения одинаковы) отвергается. Если же фактическая величина критерия Т больше или равна табличной (ТЭ ≥ ТT), нулевая гипотеза сохраняется и различие между выборками считается статистически недостоверным. Следует обратить внимание на то обстоятельство, что для многих непараметрических статистик вывод о достоверности отличий делается в случае, если расчетное значение критерия меньше табличного, тогда как параметрические статистики дают заключения о значимости различий, когда расчетная величина критерия больше табличной.
Задание 4. Сравнение двух выборок по характеру распределения признака с помощью «критерия согласия» или критерия χ2 Пирсона.
(а – А)2
χ2 = ∑ --------------
А
а- наблюдаемые частоты; А – теоретические частоты.
Перед расчетом значения критерия следует убедиться, что выполнены следующие требования к данным для расчета критерия χ2:
– объем выборки более 30 вариант, n>30,
– суммы эмпирических и теоретических частот равны объему выборки n = Σa = ΣA (с точностью не ниже 1–2%),
|
|
|
– все классы эмпирического и теоретического рядов имеют частоты более 4, aj>4; если какие-либо классы имеют меньше 4 вариант, то они должны быть объединены (суммированы) с соседними.
- степень свободы, от которой зависит величина критерия вычисляется по формуле:
k = ni – 3, где ni – число классов вариационного ряда.
Следует помнить, если варианты в конечных классах суммируются, то за ni принимается число классов уже объединённых вариант!
Достаточно хорошо известная вышеприведённая формула позволяет соотнести полученное (эмпирическое) распределение признаков с теоретически возможным в соответствии с разными законами распределений, в зависимости от которых А вычисляется по разным формулам. Однако рассматриваемый критерий можно использовать и для проверки соответствия друг другу двух эмпирических выборок. В этом случае для расчёта используются формулы, выведенные из уже предложенной, единственным условием использования для этой цели критерия является то, что частоты обоих вариационных рядов должны распределяться в границах одних и тех же классов, а сами варианты должны быть выражены не в относительных единицах (не % и не доли, например). Формулы принимают вид:
для равноразмерных выборок (n1 = n2)
p12
χ2 = 4(∑----------)-N
p1+p2
для неравных выборок (n1 ≠ n2)
N2 p12 n12
χ2 = ----- (∑-------- - ------)1
n1n2 p1+p2 N
p1, p2 – частоты сравниваемых распределений; n1, n2 – объём выборок; N – общий объём двух выборок.
Если полученный результат критерия превышает стандартный, то нулевая гипотеза отвергается.
1) Урожай фасоли, полученный от посева на делянках от крупных (p1) и мелких (p2) семян, распределился следующим образом:
| масса семян, мг | частоты | p12 | р1+р2 | р12 / (р1+р2) | |
| p1 | p2 | ||||
| сумма |
Определите, имеет ли значение, какого размера высаживать семена.
2) Изучали основной вид очанки (Euphrasia pralcurta Chitr.) и одну из её разновидностей (E. ssp. curta Fr.). Анализ вида производили по числу растений, зацветающих из того или иного (по счёту) узла. Нужно выяснить, в какой мере основной вид очанки отличается от её разновидности, что имеет прямое отношение к проблеме видообразования, совершающегося в природе. Результаты приведены в таблице:
|
|
|
| количество узлов на стеблях растений | частоты | p12 | р1+р2 | р12 / (р1+р2) | |
| p1 | p2 | ||||
| сумма |
Можно ли обе популяции очанки считать принадлежащими к одному виду?
Задание 5. Сравнение выборок по непараметрическому критерию Колмогорова-Смирнова (λ). С помощью данного критерия можно оценить только очень большие выборки (n≥100). Стандартные значения критерия, соответствуют трём порогам доверительной вероятности: при Р1=0.95 λ=1.36; при Р2=0.99 λ=1.63; при Р3=0.999 λ=1.95. Нулевая гипотеза отвергается, если полученные значения критерия превосходят теоретические при заданном пороге доверительной вероятности. Вычисления проводят по формуле:
для равноразмерных выборок (n1 = n2)
λ= (∑р1 - ∑р2)max / √n
для неравных выборок (n1 ≠ n2)
 λ = ((∑р1/n1) – (∑р2/n2))max* √(n1n2 / (n1+n2))
λ = ((∑р1/n1) – (∑р2/n2))max* √(n1n2 / (n1+n2))
∑p – накопленные частоты первой и второй выборок (к сумме частот предыдущей строчки прибавляется частота следующей); n – объём выборок (n1 = n2).
1) Произведите расчет для примера с размером семян фасоли.
| масса семян, мг | частоты | ∑p1 | ∑р2 | ∑р1-∑р2 | |
| p1 | p2 | ||||
| сумма |
2) Проверьте соответствие разновидности очанки основному виду.
| количество узлов на стеблях растений | частоты | ∑p1 | ∑р2 | ∑р1-∑р2 | |
| p1 | p2 | ||||
| сумма |





|
|
|


