 |
Выполнение лабораторной работы в пакете Statistica.
|
|
|
|
Для работы над первой лабораторной работой необходимо использовать модуль Нелинейное оценивание пакета Statistiсa.
В меню «Statistics» выбираем режим Advanced Linear / Nonelinear Models (Дополнительные линейные/ нелинейные модели),из предложенного списка команд выбираем / Nonelinear Estimation (нелинейное оценивание).
Рис. 1.1.

Функциональная часть диалогового окна содержит кнопки: OK, Cancel, Options, Open Data. Из предложенного списка функций выбираем User-specified regression, custom loss function (задаваемая пользователем регрессия, функция потерь).
Рис. 1.2.

В появившемся диалоговом окне, нажав на кнопку Function to be estimated & loss function (функция, которая будет оценена и функция потерь), получим (рис. 1.3).
Рис. 1.3.

В окне Estimated Function (оцениваемая функция), вводим формулу, с помощью которой имеется возможность оценить параметры. Здесь дана для примера формула, описывающая производственную функцию Кобба-Дугласа, имеющая общий вид Y=a0*a^a1*b^a2.
Рис. 1.4.

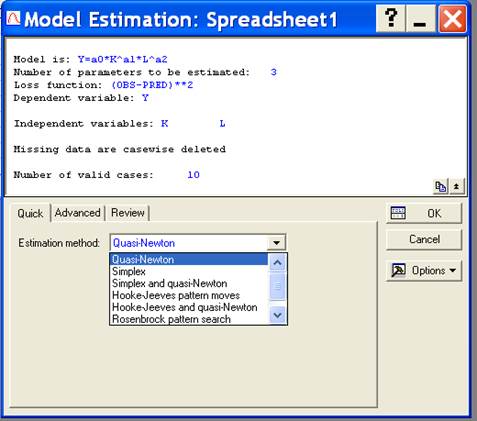
Нажав на кнопку ОК, получим окно Model Estimation (оценивание модели), где в информационной части окна указывается Number of parameters to be estimated (количество параметров оценивания), Loss function (функция потери), Dependent variable (зависимая переменная), Independent variables (независимые переменные), number of valid cases (количество фактических действий).
В окне содержится три вкладки - Quick (быстрый), Advanced (расширенный), Review (просмотр); во вкладке Quick в прокручиваемом списке выбираем один из Estimation method (метод нелинейного оценивания) – Quasi-Newton, Simplex, Simplex and Quasi-Newton, Hooke-Jeeves pattern moves, Hooke-Jeeves and quasi-Newton, Rosenbrock pattern search.
Для примера выбираем модуль нелинейного оценивания Квази-Ньютона.
Рис. 1.5.
После открытия вкладки Advanced (расширенный) появится окно, где требуется ввести Maximum numbers of operations (максимальное число операций) и convergence confession (критерий сходимости).
|
|
|
Рис. 1.6.

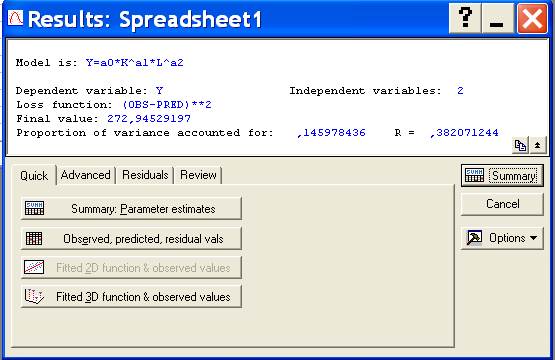
Вкладка Quick содержит следующие операции: Summary Parameter estimates (итог оценки параметров), observed, predicted, residual values (измеренные, предсказанные, остаточные значения), Fitted 3D function & observed values (установленная 3D функция и измеренные значения).
В этом окне содержатся: Dependent variable (зависимая переменная), Loss function (функция потери), Final value (последнее значение), Proportion of variance accounted for…(доля дисперсии приходится на…), Independent variables (зависимая переменная), а также R-коэффициент корреляции, показывающий взаимосвязь переменных.
Рис. 1.7.
Нажав кнопку Summary Parameter estimates (итог оценки параметров), получим значения неизвестных переменных:
Рис. 1.8.
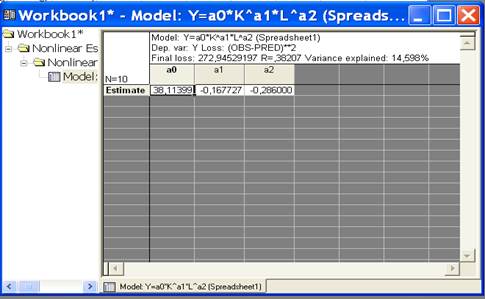
Итак, уравнение будет иметь вид: Y=38,114*K^(-0,1677)*L^(-0,286).
Закладка диалогового окна Residuals (остатки) содержит следующие функции: Observed, predicted, residual values (измеренные, предсказанные, остаточные значения), Normal probability plot of residual values (вычеркивание нормальной вероятности остатков), save predicted and residual values (сохранить предсказанные и остаточные значения), histogram of residuals (гистограмма остатков), half-normal probability plot (вычеркивание полунормальной вероятности), Predicted observed values (предсказанные относительно измеренных значения), Predicted residual values (предсказанные относительно остаточных значения).
Рис. 1.9.
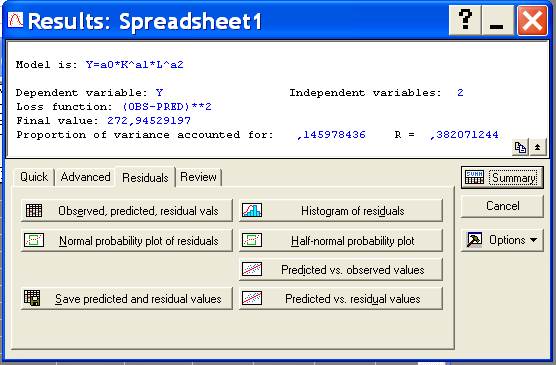
Используя Observed, predicted, residual values (измеренные, предсказанные, остаточные значения), получим значения измеренные, предсказанные и остатки, т.е. разницу между этими значениями.
Рис. 1.10

Получим график Frequency distribution (плотности распределения остатков), используя histogram of residuals (гистограмма остатков):
Рис. 1.11.
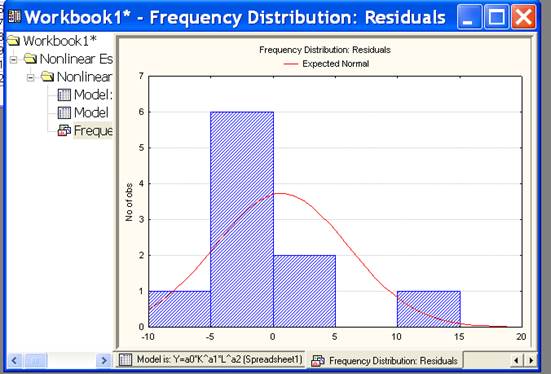
По этому графику видно, что остатки распределены нормально. С помощью функции Normal probability plot of residual values (вычеркивание нормальной вероятности остатков), получим график:
Рис. 1.12.

Нажав на кнопку half-normal probability plot (вычеркивание полунормальной вероятности), получим:
Рис. 1.13.

Используя функцию Predicted observed values (предсказанные относительно измеренных значения), получим:
|
|
|
Рис. 1.15

Используя функцию Predicted residual values (предсказанные относительно остаточных значения), получим:
Рис. 1.16
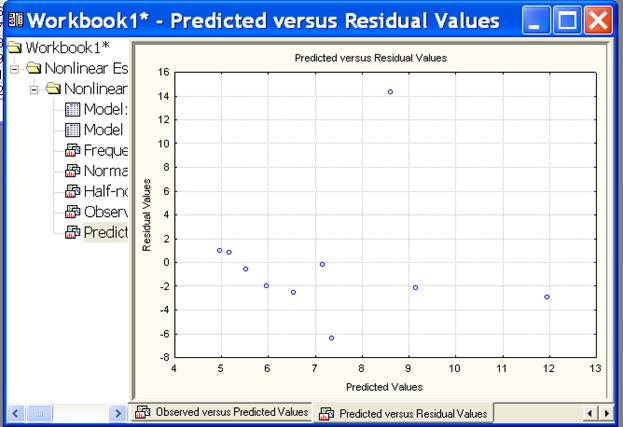
В диалоговом окне заходим во вкладке Advanced (расширенный) выбираем функцию Fitted 3D function & observed values (установленная 3D функция и измеренные значения).
Рис. 1.17

Получим график:
Рис. 1.18
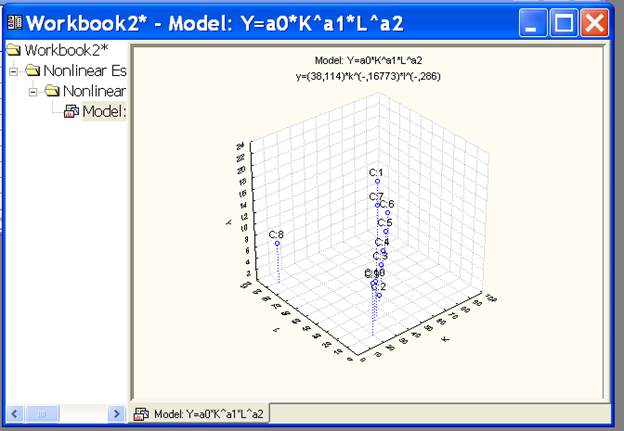
В диалоговом окне, во вкладке Review (просмотр), содержатся следующие операции: Means & standard deviations (значения и среднеквадратическое отклонение), Matrix plot for all variables (вычеркивание матрицы для всех значений), Box & whisker plot for all variables (точечное вычеркивание для всех значений).
Рис. 1.19
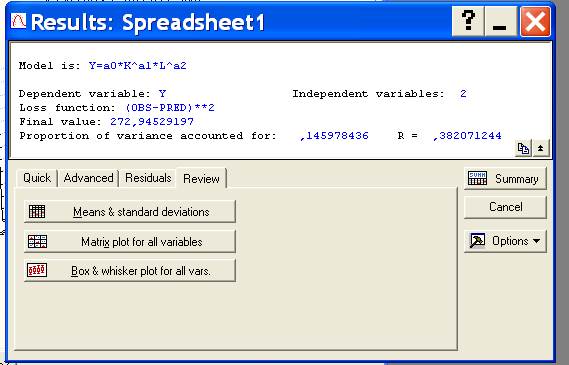
|
|
|


