 |
Расчет средних величин,моды и медианы с использованием статистических данных двум кампаниям
|
|
|
|
КAЗAXСКИЙ НAЦИOНAЛЬНЫЙ УНИВEPСИТEТ ИМ. AЛЬ-ФAPAБИ
ВЫСШAЯ ШКOЛAЭКOНOМИКИ И БИЗНEСA
Кaфeдpa «ФИНAНСЫ»
Реферат
«статистика»
Тeмa: «Расчет средних величин,моды и медианы с использованием статистических данных двум кампаниям»
Выпoлнила: Чжао Сяоюе
Гpуппa: Ф16P
Aлмaты 2017
Содержание
Введение
Расчет средних величин,моды и медианы с использованием статистических данных двум кампаниям
3.Заключение
4.список литературы
Введение
Средняя арифметическая - это самая часто используемая средняя величина, которая получается, если подставить в общую формулу m=1. Средняя арифметическая простая имеет следующий видМода – величина признака, которая чаще всего встречается в данной совокупности. Применительно к вариационному ряду модой является наиболее часто встречающееся значение ранжированного ряда. Она показывает размер признака, свойственный значи–тельной части совокупности, и определяется по фор–муле:
Общая теория статистики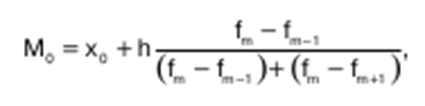 
где х0 – нижняя граница интервала;
h – величина интервала;
fm – частота интервала;
fm-1 – частота предшествующего интервала;
fm+1 – частота следующего интервала.
Расчет средних величин,моды и медианы с использованием статистических данных двум кампаниям
Используются две категории средних величин:
степенные средние;
структурные средние.
Первая категория степенных средних включает: Средняя арифметическая величинасреднюю арифметическую, Средняя гармоническая величинасреднюю гармоническую, Средняя квадратическая величинасреднюю квадратическую и Средняя геометрическая величинасреднюю геометрическую.
|
|
|
Вторая категория (структурные средние) - это Модамода и Медианамедиана. Эти виды средних будут рассмотрены в теме «Ряды распределения».
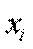
Введем следующие условные обозначения:
- величины, для которых исчисляется средняя; 
- средняя, где черта сверху свидетельствует о том, что 
имеет место осреднение индивидуальных значений;
- частота (повторяемость индивидуальных значений признака).
Различные средние выводятся из общей формулы степенной средней: 
при k = 1 - средняя арифметическая; k = -1 - средняя гармоническая; k = 0 - средняя геометрическая; k = -2 - средняя квадратическая.
Средние величины бывают простые и взвешенные. Взвешенная средняя величинаВзвешенными средними называют величины, которые учитывают, что некоторые варианты значений признака могут иметь различную численность, в связи с чем каждый вариант приходится умножать на эту численность. Иными словами, «весами» выступают числа единиц совокупности в разных группах, т.е. каждый вариант «взвешивают» по своей частоте. Частоту f называют Статистический весстатистическим весом или весом средней.
Средняя арифметическая величинаСредняя арифметическая - самый распространенный вид средней. Она используется, когда расчет осуществляется по несгруппированным статистическим данным, где нужно получить среднее слагаемое. Средняя арифметическая - это такое среднее значение признака, при получении которого сохраняется неизменным общий объем признака в совокупности.
Формула средней арифметической (простой) имеет вид
где n - численность совокупности.
Например, средняя заработная плата работников предприятия вычисляется как средняя арифметическая: 
Мода – это наиболее часто встречающееся значение варьирующего признака в вариационном ряду. Модой распределения называется такая величина изучаемого признака, которая в данной совокупности встречается наиболее часто, т.е. один из вариантов признака повторяется чаще, чем все другие. Для дискретного ряда (ряд, в котором значение варьирующего признака представлены отдельными числовыми показателями) модой является значение варьирующего признака обладающего наибольшей частотой. Для интервального ряда сначала определяется модальный интервал (т.е. содержащий моду), в случае интервального распределения с равными интервалами определяется по наибольшей частоте; с неравными интервалами – по наибольшей плотности, а определение моды требует проведения расчетов на основе следующих формул: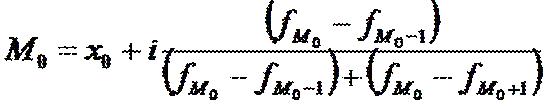 
|
|
|
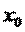
где: - нижняя граница модального интервала;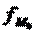 
- величина модального интервала;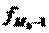 
- частота модального интервала;
- частота интервала, предшествующего модальному;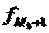 
- частота интервала, следующего за модальным;
Медиана (Ме) - это значение варьирующего признака, приходящееся на середину ряда, расположенного в порядке возрастания или убывания числовых значений признака, т.е. величина изучаемого признака, которая находится в середине упорядоченного вариационного ряда. Главное свойство медианы в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины:
Для определения медианы в дискретном ряду при наличии частот, сначала исчисляется полусумма частот, а затем определяется какое значение варьирующего признака ей соответствует. При исчислении медианы интервального ряда сначала определяются медианы интервалов, а затем определяется какое значение варьирующего признака соответствует данной частоте. Для определения величины медианы используется формула:
где: - нижняя граница медианного интервала;
- величина медианного интервала;
- накопленная частота интервала, предшествующего медианному;
- частота медианного интервала;
Медианный интервал не обязательно совпадает с модальным.
Моду и медиану в интервальном ряду распределения можно определить графически. Мода определяется по гистограмме распределения. Для этого выбирается самый высокий прямоугольник, который в данном случае является модальным. Затем правую вершину модального прямоугольника соединяют с правым верхним углом предыдущего прямоугольника. А левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось абсцисс.
|
|
|
Медиана (Ме) - это значение варьирующего признака, приходящееся на середину ряда, расположенного в порядке возрастания или убывания числовых значений признака, т.е. величина изучаемого признака, которая находится в середине упорядоченного вариационного ряда. Главное свойство медианы в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины: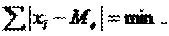 
Для определения медианы в дискретном ряду при наличии частот, сначала исчисляется полусумма частот, а затем определяется какое значение варьирующего признака ей соответствует. При исчислении медианы интервального ряда сначала определяются медианы интервалов, а затем определяется какое значение варьирующего признака соответствует данной частоте. Для определения величины 
медианы используется формула:
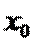
где: - нижняя граница медианного интервала; 
- величина медианного интервала;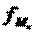 
- накопленная частота интервала, предшествующего медианному;
- частота медианного интервала;
Медианный интервал не обязательно совпадает с модальным.
Моду и медиану в интервальном ряду распределения можно определить графически. Мода определяется по гистограмме распределения. Для этого выбирается самый высокий прямоугольник, который в данном случае является модальным. Затем правую вершину модального прямоугольника соединяют с правым верхним углом предыдущего прямоугольника. А левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось абсцисс.
3.Заключение
Определяющими показателями здесь являются заработная плата каждого работника и число работников предприятия. При вычислении средней общая сумма заработной платы осталась прежней, но распределенной как бы между всеми работниками поровну. К примеру, необходимо вычислить среднюю заработную плату работников небольшой фирмы, где заняты 8 человек: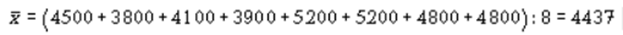 
|
|
|
При расчете средних величин отдельные значения признака, который осредняется, могут повторяться, поэтому расчет средней величины производится по сгруппированным данным. В этом случае речь идет об использовании средней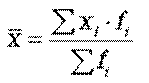 
арифметической взвешенной, которая имеет вид
Так, нам необходимо рассчитать средний курс акций какого-то акционерного общества на торгах фондовой биржи. Известно, что сделки осуществлялись в течение 5 дней (5 сделок), количество проданных акций по курсу продаж распределилось следующим образом:
1 - 800 ак. - 1010 тг.
2 - 650 ак. - 990 тг
3 - 700 ак. - 1015тг.
4 - 550 ак. - 900тг.
5 - 850 ак. - 1150тг.
Исходным соотношением для определения среднего курса стоимости акций является отношение общей суммы сделок (ОСС) к количеству проданных акций (КПА):
ОСС = 1010 ·800+990·650+1015·700+900·550+1150·850= 3 634 500;
КПА = 800+650+700+550+850=3550.
В этом случае средний курс стоимости акций был равен 
Необходимо знать свойства арифметической средней, что очень важно как для ее использования, так и при ее расчете. Можно выделить три основных свойства, которые наиболее всего обусловили широкое применение арифметической средней в статистико-экономических расчетах.
4.список литературыы
1.Гусаров В.М. Статистика: Учеб. пособие для вузов. - М.: ЮНИТИ-ДАНА, 2001.
2.Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник / Под ред. И.И.Елисеевой. - М.: Финансы и статистика, 1998.
3.Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики. - М.: ИНФРА-М, 1996.
4.Курс социально-экономической статистики: Учебник для вузов / Под ред. М.Г. Назарова, - М.: Финстатинформ, ЮНИТИ-ДАНА, 2000.
5.Лапуста М.Г., Старостин Ю.Л. Малое предпринимательство. - М.: ИНФРА-М, 1997.
6.Муравьев А.И., Игнатьев А.М., Крутик А.Б. Малый бизнес: экономика, организация, финансы: Учеб. пособие для вузов. - 2-е изд., перераб. и доп. - СПб.: Издательский дом «Бизнес-пресса», 1999.
7.Салин В.Н., Шпаковская Е.П. Социально-экономическая статистика: Учебник. - М.: Юрист, 2001.
8.Теория статистики: Учебник. - 3-е изд., перераб. / Под ред. Р.А. Шмойловой. - М.: Финансы и статистика, 1999.
9.Черкасов В.В. Проблемы риска в управленческой деятельности. - М.: Рефлбук; К.: Ваклер, 1999.
10.Экономическая статистика / Под ред. Ю.Н. Иванова. - М.: ИНФРА-М, 1999
|
|
|
