Уравнение плоскости в отрезках. Неполные уравнения плоскости.

Вопрос № 64

 

 

 

Уравнение плоскости в отрезках. Неполные уравнения плоскости.

Исследование общего уравнения плоскости

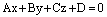, (7)

где 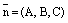– координаты ее нормального вектора, производится аналогично исследованию общего уравнения прямой на плоскости. Приведем ниже все случаи.

Если 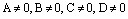, то уравнение (7) может быть записано в виде уравнения плоскости в отрезках:

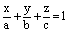(10)

– плоскость, отсекающая от осей координат отрезки величиной а, b и с соответственно, где обозначено

.

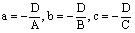рис.6.

Определение. Уравнение

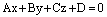
называется неполным уравнением плоскости, если хотя бы один из его коэффициентов А, В, С, D равен нулю.

Если 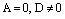, то уравнение (7) имеет вид

. (11)

В координатной плоскости Оуz это уравнение есть уравнение прямой, а так как 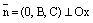, то данная плоскость параллельна оси Ох. Уравнение (11) может быть записано в виде

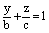(12)

или 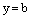– уравнение плоскости параллельной координатной плоскости Охz и отсекающей от оси Оу отрезок величины b,

или 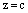– уравнение плоскости параллельной координатной плоскости Оху и отсекающей от оси Оz отрезок величины с.

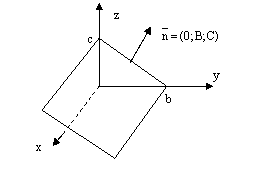
рис.7.

рис.8.

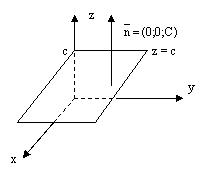
рис.9.

Если , то уравнение (6) имеет вид

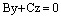. (13)

Это уравнение прямой в координатной плоскости Оуz, проходящая через начало координат и в то же время уравнение плоскости, содержащей ось Ох.

рис.10.

Если в уравнении (13) 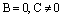, то получаем

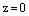
– уравнение координатной плоскости Оху.

Если в уравнении (13) , то получаем

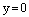
– уравнение координатной плоскости Охz.

Ситуации, когда 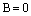или 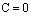исследуются аналогично.

Подведем итог исследованию общего уравнения плоскости

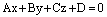. (7)

1) Если 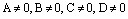, то можно уравнение (7) записать в виде уравнения в отрезках

,

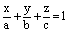где а, b, с – величины отсекаемых плоскостью от координатных осейотрезков.

2) Если 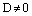, но один из коэффициентов А, В, С равен нулю, то получаем уравнение плоскости в виде

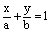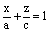или или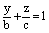

– плоскость параллельная оси Оz или Оу или Ох соответственно.

3) Если 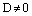, но два из коэффициентов А, В, С равны нулю, то получаем уравнение плоскости в виде

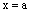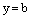или или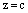

– соответственно плоскость параллельна координатной плоскости Оуz или Охz или Оху.

4) Если 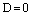, то уравнение (7) принимает вид

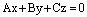
– плоскость содержит начало координат.

5) Если 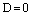и один из коэффициентов А, В, С равен нулю, то получаем уравнение плоскости в виде

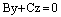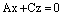или или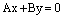

– плоскость содержит соответственно ось Ох или ось Оу или ось Оz.

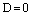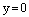6) Если и два из коэффициентов А, В, С равны нулю, то получаем уравнение плоскости в виде или или 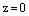– уравнение соответственно координатных плоскостей Оуz или Охz или Оху.

п.6. Нормированное уравнение плоскости и прямой на плоскости.

Пусть

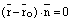(1)

– векторное уравнение плоскости или прямой на плоскости, где – нормальный вектор плоскости (прямой), 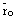– радиус-вектор фиксированной точки плоскости (прямой), 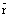– радиус-вектор текущей точки плоскости (прямой).

Заметим, что в уравнении (1) длина нормального вектора не играет никакой роли. Выберем в уравнении (1) в качестве нормального вектора нормальный вектор единичной длины 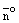, а направление нормальноговектора

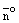выберем такое, чтобы угол между вектором и был острый. Смотри следующие рисунки.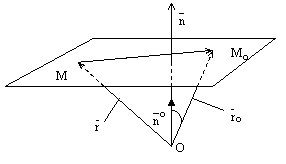

рис.11.

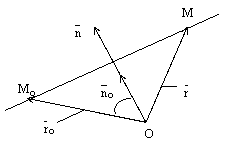
рис.12.

Иначе, направление вектора 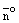должно быть от начала координат к плоскости (прямой). Раскроем в уравнении (1) скобки

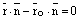
и разделим обе части уравнения на 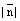, если скалярное произведение 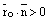или на , если 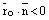. Получим

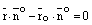, (14)

где .

Обозначим 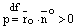и пусть 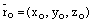, 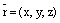. Так как координатами единичного вектора являются его направляющиекосинусы, то 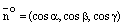. Подставляя в (14), получаем

.

Определение. Уравнение вида

, (15)

где 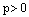, – направляющие косинусы нормального вектораплоскости, называется нормированным (нормальным) уравнением плоскости.

В случае прямой на координатной плоскости Оху имеем: 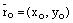, , 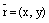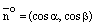и

.

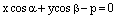Определение. Уравнение вида

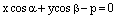, (16)

где 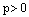, 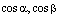– направляющие косинусы нормального векторапрямой, называется нормированным (нормальным) уравнением прямойна координатной плоскости Оху.

Заметим, что в уравнениях (15) и (16) свободный коэффициент (– р) отрицательный, р численно равно расстоянию от начала координат до плоскости (прямой):

.

В этом заключается геометрический смысл свободного члена р в этих уравнениях.

Пример. Записать нормированное уравнение плоскости, если его общее уравнение имеет вид:

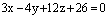
и найти расстояние от начала координат до плоскости.

Решение. Имеем, , .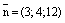

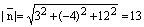Так как свободный коэффициент этого уравнения равен положительному числу 26, то для получения нормированного уравнения плоскости разделим обе части общего уравнения на число, противоположное модулю нормального вектора:

.

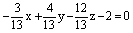Ответ: 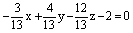– нормированное уравнение плоскости.Расстояние

от начала координат до плоскости равно 2.

Аналогично приводится к нормальному виду общее уравнение прямой.

 

Поделиться:

Воспользуйтесь поиском по сайту: