 |
Основные показатели динамики экономических показателей
|
|
|
|
Для количественной оценки динамики явлений применяются статистические показатели: абсолютные приросты, темпы роста, темпы прироста, которые могут быть цепными, базисными или средними.
В основе расчета этих показателей динамики лежит сравнение уровней
временного ряда.
Если сравнение осуществляется с одним и тем же уровнем, принятым за базу сравнения, то эти показатели называются базисными.
Если сравнение осуществляется при переменной базе, и каждый последующий уровень сравнивается с предыдущим, то вычисленные таким образом показатели называются цепными.
Абсолютный прирост равен разности двух сравниваемых уровней.
Темп роста есть отношение двух сравниваемых уровней ряда, выраженное в процентах. Темп прироста характеризует абсолютный прирост в относительных величинах. Определенный в процентах, темп прироста показывает, на сколько процентов изменился сравниваемый уровень по отношению к уровню, принятому за базу сравнения. В таблице 2.4 приведены формулы для вычисления базисных, цепных и средних показателей динамики. Средние показатели: средний абсолютный прирост, средний темп роста и прироста определяются для получения обобщающих показателей динамики развития.
В таблице использованы следующие обозначения:1,y2,...,yt,..., yn - уровни временного ряда в моменты времени t = 1, 2,..., n;- длина временного ряда; yб - уровень временного ряда, принятый за базу.
Таблица 2.4 Основные показатели динамики временных рядов
| Показатель | Абсолютный прирост, Δу | Темп роста, Т, % | Темп прироста К, % |
| Цепной |   
| ||
| Базисный |   
| ||
| Средний |   
|
Прогнозирование на основе средних показателей динамики
|
|
|
Описание динамики ряда с помощью среднего абсолютного прироста соответствует его представлению в виде прямой, проведенной через две крайние точки. В этом случае, чтобы получить прогноз на один шаг вперед, достаточно к последнему наблюдению прибавить значение среднего абсолютного прироста:
(2.7)
где yn - фактическое значение в последней n- ой точке ряда;
- прогнозная оценка значения уровня в точке n+1;
- значение среднего прироста, рассчитанное для временного ряда 
.
Чтобы получить прогноз на К шагов вперед, нужно к последнему наблюдению прибавить значение среднего абсолютного прироста, умноженное на К:
(2.8)
Такой подход к получению прогнозного значения корректен, если характер развития близок к линейному. На такой равномерный характер развития могут указывать примерно одинаковые значения цепных абсолютных приростов.
Применение среднего темпа роста (и среднего темпа прироста) для описания динамики ряда соответствует его представлению в виде показательной или экспоненциальной кривой, проведенной через две крайние точки. Использование этого показателя для прогноза целесообразно для процессов, изменение динамики которых происходит примерно с постоянным темпом роста. В этом случае прогнозное значение на К шагов вперед может быть получено по формуле:
(2.9)
где 
- прогнозная оценка значения уровня ряда в точке n+к;n- фактическое значение в последней n-ой точке ряда;
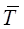- средний темп роста, рассчитанный для ряда 
(в относительных единицах).
К недостаткам среднего прироста и среднего темпа роста следует отнести то, что они учитывают лишь конечный и начальный уровни ряда, исключают влияние промежуточных уровней. Тем не менее, эти показатели имеют широкую область применения, что объясняется простотой их вычисления. Они могут быть использованы как приближенные, простейшие способы прогнозирования, предшествующие более глубокому количественному и качественному анализу.
|
|
|
Прогнозирование по методу экспоненциальных средних
В настоящее время одним из наиболее перспективных направлений исследования и прогнозирования одномерных временных рядов являются адаптивные методы.
При обработке временных рядов, как правило, наиболее ценной является информация последнего периода, т.к. необходимо знать, как будет развиваться тенденция, существующая в данный момент, а не тенденция, сложившаяся в среднем на всем рассматриваемом периоде. Адаптивные методы позволяют учесть различную информационную ценность уровней временного ряда, степень "устаревания" данных.
Прогнозирование методом экстраполяции на основе кривых роста в какой-то мере тоже содержит элемент адаптации, поскольку с получением "свежих" фактических данных параметры кривых пересчитываются заново.
Поступление новых данных может привести и к замене выбранной ранее кривой на другую модель. Однако степень адаптации в данном случае весьма незначительна, кроме того, она падает с ростом длины временного ряда, т.к. при этом уменьшается "весомость" каждой новой точки. В адаптивных методах различную ценность уровней в зависимости от их "возраста" можно учесть с помощью системы весов, придаваемых этим уровням.
Оценивание коэффициентов адаптивной модели обычно осуществляется на основе рекуррентного метода, который формально отличается от метода наименьших квадратов, метода максимального правдоподобия и других методов тем, что не требует повторения всего объема вычислений при появлении новых данных.
Примером простейшей адаптивной модели является экспоненциальная средняя. Экспоненциальное сглаживание временного ряда производится итеративно (пошагово), причем массив прошлой информации представлен единственным значением сглаженного уровня ряда в предыдущий момент времени.
Для экспоненциального сглаживания ряда используется рекуррентная формула
|
|
|
(2.10)
где St- значение экспоненциальной средней в момент t;
α - параметр сглаживания, α =сonst, 0< α <1;
β = 1- α.
Если последовательно использовать соотношение (2.10), то экспоненциальную среднюю St можно выразить через предшествующие значения уровней временного ряда. При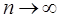 
(2.11)
Таким образом, величина St является взвешенной суммой всех членов ряда. При этом, веса отдельных уровней ряда убывают по мере их удаления в прошлое соответственно экспоненциальной функции (в зависимости от "возраста" наблюдений). Поэтому величина St названа экспоненциальной средней.
Например, если α = 0,3, то вес текущего наблюдения yt будет равен 0,3; вес предыдущего уровня yt-1 будет соответствовать α*β = 0,3*0,7=0,21; для уровня yt-2 вес составит α*β2 = 0,3*0,72=0,147; для yt-3 вес α*β3 = 0,3*0,73 = 0,1029 и т.д.
Пусть модель временного ряда имеет вид:
.
Английский математик Р. Браун показал, что дисперсия экспоненциальной средней D[St] меньше дисперсии временного ряда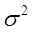 
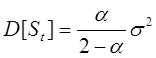(2.12)
Из (2.12) следует, что при высоком значении α дисперсия экспоненциальной средней незначительно отличается от дисперсии ряда. С уменьшением α дисперсия экспоненциальной средней уменьшается, возрастает ее отличие от дисперсии ряда. Тем самым, экспоненциальная средняя начинает играть роль «фильтра», поглощающего колебания временного ряда.
Таким образом, с одной стороны, необходимо увеличивать вес более свежих наблюдений, что может быть достигнуто повышением α, с другой стороны, для сглаживания случайных отклонений величину α нужно уменьшить.
Эти два требования находятся в противоречии. Поиск компромиссного значения параметра сглаживания α составляет задачу оптимизации модели.
Часто поиск оптимального значения α осуществляется путем перебора и в качестве оптимального выбирается такое значение, при котором получена наименьшая дисперсия ошибки. Обычно параметр сглаживания принимается равным в интервале от 0,1 до 0,3.
|
|
|
При использовании экспоненциальной средней для краткосрочного прогнозирования предполагается, что модель ряда имеет вид: yt = a1,t + et, где a1,t - варьирующий во времени средний уровень ряда, et - случайные не автокоррелированные отклонения с нулевым математическим ожиданием и дисперсией .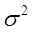
Прогнозная модель определяется равенством
где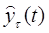 
- прогноз, сделанный в момент t на τ единиц времени (шагов) вперед; 
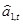- оценка параметра в момент времени t.
Единственный параметр модели â1,t определяется экспоненциальной средней: â 1,1 = St ; â 1,0 = S0.
Выражение (2.10) можно представить иначе:
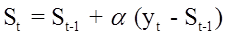(2.13)
Величину 
можно рассматривать как погрешность прогноза. Тогда новый прогноз St получается в результате корректировки предыдущего прогноза с учетом его ошибки. В этом и состоит адаптация модели.
Экспоненциальное сглаживание является примером простейшей самообучающейся модели. Массив прошлой информации уменьшен до единственного значения St-1.
Глава II Задача
Представлены данные об остатках оборотных средств за 15 месяцев. Остатки даны на начало года. Необходимо рассчитать прогноз остатков на начало 16-го месяца, исходя из предложения, что тенденция ряда может быть описана
а) линейной моделью y1=a0+a1t
б) параболической моделью yt=a0+a1t+a2t2
| № п/п | Yt (тыс.р.) | t | Yt*t | t2 | Yt*t2 | t4 |
| 1 | 650 | -7 | - 4550 | 49 | 31850 | 2401 |
| 2 | 700 | -6 | - 4200 | 36 | 25200 | 1296 |
| 3 | 715 | -5 | - 3575 | 25 | 17875 | 625 |
| 4 | 700 | -4 | - 2800 | 16 | 11200 | 256 |
| 5 | 650 | -3 | - 1950 | 9 | 5850 | 81 |
| 6 | 550 | -2 | - 1100 | 4 | 2200 | 16 |
| 7 | 610 | -1 | - 610 | 1 | 610 | 1 |
| 8 | 700 | 0 | 0 | 0 | 0 | 0 |
| 9 | 650 | 1 | 650 | 1 | 650 | 1 |
| 10 | 630 | 2 | 1260 | 4 | 2520 | 16 |
| 11 | 600 | 3 | 1800 | 9 | 5400 | 81 |
| 12 | 710 | 4 | 2840 | 16 | 11360 | 256 |
| 13 | 750 | 5 | 3750 | 25 | 18750 | 625 |
| 14 | 760 | 6 | 4560 | 36 | 27360 | 1296 |
| 15 | 770 | 7 | 5390 | 49 | 37730 | 2401 |
| Итого: | 10145 | 0 | 1465 | 280 | 198555 | 9352 |
Решение
А) В предположении об изменении тенденции ряда по линейной модели:
- определить параметры линейного тренда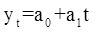 
;
дать экономическую интерпретацию полученных параметров модели;
рассчитать прогнозный уровень выручки от продаж за 16-й месяц.
Б) В предположении об изменении тенденции ряда по параболической модели:
определить параметры параболического тренда 
;
дать экономическую интерпретацию полученных параметров модели;
рассчитать прогнозный уровень выручки от продаж за 16-й месяц.
Расчет параметров модели производится по формулам:
Система нормальных уравнений для оценивания параметров прямой состоит из двух уравнений:
|
|
|
Для параболы второго порядка система содержит три уравнения, позволяющих найти оценки трех неизвестных коэффициентов 
:
а) Прямая. С учетом данных таблицы и выражения:
Получаем: а0 = 10145 тыс. руб. ÷ 15 = 676,333 тыс. руб.
а1 = 1465 тыс. руб. ÷ 280 = 5,232 тыс. руб.
Следовательно, уравнение линейного тренда имеет вид:
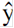t = 676,333 + 5,232 × t
Согласно полученной модели, оценка среднего уровня ряда при t = 0 составляет 676333 рублей, а среднемесячный абсолютный прирост остатка оборотных средств равен 5232 руб.
Для прогнозирования по линейной модели на одну точку вперед необходимо в полученное выражение подставить соответствующее значение временного параметра t = 8, соответствующее реальному значению t* = 16.
Прогнозное значение остатка оборотных средств на 16-й месяц составит:
= 676,333 + 5,232 × 8 = 718,189 тыс. руб.
= 718189 руб.
б) Парабола. С учетом данных таблицы и выражений:
Получаем: а1 = 1465 тыс. руб. ÷ 280 = 5,232 тыс. руб.
а2 = (15 × 198555 - 280 × 645,1) ÷ (15 × 9352 - 280²) = (2978325 - 180628) ÷ (140280 - 78400) = 2797697 ÷ 61890 = 45,204 тыс. руб.
а0 = 676,333 - 280 ÷ 15 × 45,204 = - 167,474 тыс. руб.
Полученное уравнение параболы имеет вид:
= - 167,474 + 5,232 × t + 45,204 × t²
Согласно полученной модели, оценка среднего уровня ряда при t = 0 составляет - 167474 рублей, среднемесячный абсолютный прирост остатка оборотных средств равен 5232 руб., причем прирост является не постоянной величиной, а в среднем возрастает на 45204 рублей ежемесячно.
Для прогнозирования по параболе на одну точку вперед необходимо в полученное выражение подставить соответствующее значение временного параметра tпр = 8, соответствующее реальному значению t* = 16.
Прогнозное значение остатка оборотных средств за 16-й месяц составит:
= - 167,474 + 5,232 × 8 + 45,204 × 8² = - 167,474 + 41,856 + 2893,056 = 2767,438
= 2767438 руб.
временный ряд прогнозирование показатель
Список литературы
1. «СТАТИСТИЧЕСКИЕ МЕТОДЫ ПРОГНОЗИРОВАНИЯ В ЭКОНОМИКЕ», Т.А. Дуброва, Москва, 2007г.;
2. Орлов А.И. Статистические методы прогнозирования. - В кн.: Малая российская энциклопедия прогностики. - М.: Институт экономических стратегий, 2007. - С.148-153;
. «Основы экономического и социального прогнозирования: Учебник для ВУЗов». - М: ВШ, 1995;
. Четыркин Б.М. «Статистические методы прогнозирования». - М.: Статистика, 1996;
. Басовский М.К. «Прогнозирование и планирование в условиях рынка: Учебное пособие». - М.: Инфра-М, 2003. - 260 с.
|
|
|
