Виды производственных функций ПФ Кобба – Дугласа, ПФ Леонтьева, ПФ Солоу, Линейная ПФ.

Предположим, что фирма производит n видов продуктов. Виды продуктов будем обозначать индексом j, а их количества - через . Технология производства каждого вида продукта требует использования ряда ресурсов в некоторых количествах. Двойными индексами обозначим виды ресурсов, используемых для выпуска продукта вида j. Пусть .. Обозначим через - количества этих ресурсов, . Следовательно, имеется всего видов ресурсов.

Использование такой двойной индексации привлекательно с точки зрения информативности (видно, какой ресурс относится к какому продукту), но неудобно чисто технически. Во-первых, усложняется запись формул; во-вторых, увеличивается размерность задачи (т.к. среди могут быть одни и те же наименования) и, в-третьих, такие операции как сложение, вычитание затрат в векторной форме, а также составление уравнений становятся невозможными без дополнительных преобразований индексов (идентификация, упорядочение и т.д.).

Поэтому в дальнейшем виды ресурсов будем обозначать одинарными индексами k, их количества - 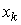, где 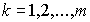. Здесь m - достаточно большое число (равное сумме , где каждый ресурс считается только один раз). Теперь можно говорить, что для производства n видов продуктов фирма использует m видов затрат. Это не приводит к недоразумениям, так как в случае неиспользования k -го ресурса для выпуска данного продукта полагаем .

Введем в рассмотрение два вида векторов: - вектор затрат и - вектор выпуска. Положительный ортант

называется пространством затрат. Аналогично определяется пространство выпуска:

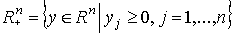
Для отражения реальных возможностей фирмы в математических моделях часто применяются более узкие множества .

Технологическая связь между затратами и выпуском описывается с помощью производственной функции.

Определение 4.1. Любая функция 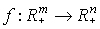, ставящая в соответствие каждому вектору затрат x вектор максимального выпуска, который может быть получен при этих затратах, называется производственной функцией.

Это есть определение производственной функции для многопродуктовой фирмы, т.е. векторной производственной функции. Если фирма выпускает только один вид продукта, то производственная функция является скалярно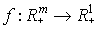й: или

В общем случае производственную функцию можно записать в неявной форме: 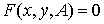, где A - -матрица параметров (технологическая матрица). В некоторых моделях применяется следующее выражение для производственной функции: 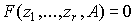, где переменные со знаком "-" обозначают затраты, а со знаком "+" - выпуски.

Если в качестве независимых переменных (аргументов) выступают затраты (см. (4.2.1)), то производственную функцию иногда называют функцией выпуска, если же фиксирована величина выпуска (y), то производственная функция является функцией затрат (). Таким образом, функция выпуска и функция затрат являются взаимно обратными друг другу функциями.

Применение производственных функций не ограничивается выявлением зависимости затраты-выпуск. Различные приемы математического аппарата позволяют использовать их для вычисления численных характеристик производства, анализа эффективности изменения масштаба производства и технологического прогресса, исследования эластичности производственных факторов, рационального ведения хозяйства, оптимального планирования и прогнозирования вариантов развития фирмы и др.

Поэтому очень важно, чтобы производственная функция объективно отражала моделируемую действительность, т.е. чтобы она удовлетворяла содержательно-логическим и экономическим требованиям. Основные из них следующие:

· в число аргументов производственной функции должны быть включены все существенные для данного процесса факторы;

· все величины должны иметь отчетливый экономический смысл;

· все экономические величины, входящие в производственную функцию, должны быть измеримы;

· выпуск продукции без затрат невозможен;

· если величина какого-либо ресурса ограничена, то выпуск не может расти бесконечно;

· увеличение затрат не может привести к уменьшению выпуска.

Вопрос об адекватном описании экономической реальности на языке производственных функций тесно связан с их математическими свойствами. Ради простоты эти свойства приведем для однопродуктового производства, т.е. для производственной функции вида (4.2.1).

1. Монотонность: из 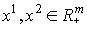и следует .

2. Вогнутость: для любых 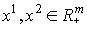и справедливо неравенство .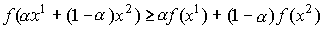

3. Поведение в начале координат: .

4. Однородность: 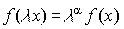, где - масштабное число, - степень однородности.

Если производственная функция дифференцируема по всем аргументам, то свойства 1 и 2 соответственно могут быть заменены следующими неравенствами:

Частные производные называются предельными продуктами. Условие (4.2.2), как и свойство 1, означает, что увеличение любого вида затрат не приводит к уменьшению выпуска. Условие (4.2.3) показывает, что увеличение затрат одного вида ресурса (при постоянном уровне затрат других ресурсов) приводит ко все меньшему приросту выпуска. Это свойство в экономической теории называется законом убывающей доходности (отдачи).

Свойство 3 является отражением бездеятельности, так как без затрат нет и выпуска. Свойство 4 описывает реакцию производства на изменение затрат. Параметр показывает масштаб изменения производства (расширения производства - если , сужения производства - если ), а - эффект от изменения масштабов производства. Если , то одновременное увеличение всех факторов в раз приводит к возрастанию объема выпуска больше, чем в раз (), т.е. эффект от расширения масштаба производства положителен. При получаем: - выпуск возрастает в той же пропорции, что и затраты. Такие функции называются линейно-однородными (или однородными в первой степени).

Если

то говорят о возрастающем (убывающем) доходе от расширения масштаба производства. Заметим, что свойство 4 определено в точке, тогда как свойства 1 и 2 - во всем пространстве затрат.

Как мы видим, перечисленные (желательные) свойства производственной функции вполне согласуются с ее определением, так как они касаются только соотношения затраты-выпуск. Действительно, здесь нет никаких требований на бесперебойную работу станков, нормирования движения конвейера и т.д. Поэтому производственная функция, как отображение количественной связи между затратами и выпуском, представляет собой регрессионную модель (см. §2.5). Следовательно, она может быть построена на основе статистических данных и с применением методов математической статистики. Оставляя подробное обсуждение этого вопроса до §4.4, сейчас мы приведем примеры наиболее удачно построенных и потому часто применяемых на практике производственных функций. При этом для простоты будем рассматривать двухфакторную однопродуктовую производственную функцию вида

Производственная функция Кобба-Дугласа. Первый успешный опыт построения производственной функции, как уравнения регрессии на базе статистических данных, был получен американскими учеными - математиком Д. Коббом и экономистом П. Дугласом в 1928 году. Предложенная ими функция изначально имела вид:

где Y - объем выпуска, K - величина производственных фондов (капитал), L - затраты труда, - числовые параметры (масштабное число и показатель эластичности). Благодаря своей простоте и рациональности, эта функция широко применяется до сих пор и получила дальнейшие обобщения в различных направлениях. Функцию Кобба-Дугласа иногда мы будем записывать в виде

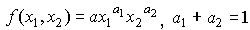
Легко проверить, что и

Кроме того, функция (4.2.4) линейно-однородна:

.

Таким образом, функция Кобба-Дугласа (4.2.4) обладает всеми вышеуказанными свойствами.

Для многофакторного производства функция Кобба-Дугласа имеет вид:

Для учета технического прогресса в функцию Кобба-Дугласа вводят специальный множитель (технического прогресса) , где t - параметр времени, - постоянное число, характеризующее темп развития. В результате функция принимает "динамический" вид:

где не обязательно . Как будет показано в следующем параграфе, показатели степени в функции (4.2.4) имеют смысл эластичности выпуска по капиталу и труду.

Производственная функция CES (с постоянной эластичностью замещения) имеет вид:

где - коэффициент шкалы, 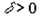- коэффициент распределения, - коэффициент замещения, - степень однородности. Если выполнены условия

то функция (4.2.5) удовлетворяет неравенствам (4.2.2) и (4.2.3) (проверьте это самостоятельно). С учетом технического прогресса функция CES записывается:

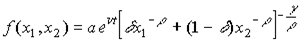
Название данной функции следует из того факта, что для нее эластичность замещения постоянна (см. §4.3).

Производственная функция с фиксированными пропорциями. Эта функция получается из (4.2.5) при и имеет вид:

Производственная функция затрат-выпуска (функция Леонтьева) получается из (4.2.6) при :

Содержательно эта функция задает пропорцию, с помощью которой определяется количество затрат каждого вида, необходимое для производства одной единицы выпускаемой продукции. Поэтому в литературе часто встречаются другие формы записи:

или

Здесь 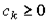- количество затрат вида k, необходимое для производства одной единицы продукции, а y - выпуск.

Производственная функция анализа способов производственной деятельности. Данная функция обобщает производственную функцию затрат-выпуска на случай, когда существует некоторое число (r) базовых процессов (способов производственной деятельности), каждый из которых может протекать с любой неотрицательной интенсивностью. Она имеет вид "оптимизационной задачи"

Здесь - выпуск продукции при единичной интенсивности j -го базового процесса, 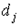- уровень интенсивности, - количество затрат вида k, необходимых при единичной интенсивности способа j. Как видно из (4.2.8), если выпуск, произведенный при единичной интенсивности и затраты, необходимые на единицу интенсивности, известны, то общий выпуск и общие затраты находятся путем сложения выпуска и затрат соответственно для каждого базового процесса при выбранных интенсивностях. Заметим, что задача максимизации функции f по 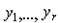в (4.2.8) при заданных ограничениях-неравенствах является моделью анализа производственной деятельности (максимизация выпуска при ограниченных ресурсах).

Линейная производственная функция (функция с взаимозамещением ресурсов) применяется при наличии линейной зависимости выпуска от затрат:

где - норма затрат k -го вида для производства единицы продукции (предельный физический продукт затрат).

 

Методы математического моделирования рисковых ситуаций. Риск и неопределенность в осуществлении экономической деятельности. Место методов математического моделирования в общей схеме управления риском. Основные механизмы управления риском — прямое воздействие на факторы риска и диверсификация. Цели моделирования механизмов управления риском. Методы моделирования неопределенности и риска экономической деятельности.

Любая сфера человеческой деятельности, в особенности эконо­мика или бизнес, связана с принятием решений в условиях неполно­ты информации. Источники неопределенности могут быть самые разнообразные: нестабильность экономической и/или политической ситуации, неопределенность действий партнеров по бизнесу, слу­чайные факторы, т.е. большое число обстоятельств, учесть которые не представляется возможным (например, погодные условия, неоп­ределенность спроса на товары, неабсолютная надежность процес­сов производства, неточность информации и др.). Экономические решения с учетом перечисленных и множества других неопределен­ных факторов принимаются в рамках так называемой теории приня­тия решений - аналитического подхода к выбору наилучшего дейст­вия (альтернативы) или последовательности действий. В зависимо­сти от степени определенности возможных исходов или последст­вий различных действий, с которыми сталкивается лицо, прини­мающее решение (ЛПР), в теории принятия решений рассматрива­ются три типа моделей:

• выбор решений в условиях определенности, если относительно каждого действия известно, что оно неизменно приводит к некото­рому конкретному исходу;

• выбор решения при риске, если каждое действие приводит к одному из множества возможных частных исходов, причем каждый исход имеет вычисляемую или экспертно оцениваемую вероятность появления. Предполагается, что ЛПР эти вероятности известны или их можно определить путем экспертных оценок;

• выбор решений при неопределенности, когда то или иное дей­ствие или несколько действий имеют своим следствием множество частных исходов, но их вероятности совершенно не известны или не имеют смысла.

Проблема риска и прибыли - одна из ключевых в экономиче­ской деятельности, в частности в управлении производством и финансами. Под риском принято понимать вероятность (угрозу) по­тери лицом или организацией части своих ресурсов, недополучения доходов или появления дополнительных расходов в результате осу­ществления определенной производственной и финансовой политики.

Различают следующие виды рисков:

· производственный, связанный с возможностью невыполнения фирмой своих обязательств перед заказчиком;

· кредитный, обусловленный возможностью невыполнения фирмой своих финансовых обязательств перед инвестором;

· процентный, возникающий вследствие непредвиденного изме­нения процентных ставок;

· риск ликвидности, обусловленный неожиданным изменением кредитных и депозитных потоков;

· инвестиционный, вызванный возможным обесцениванием ин­вестиционно-финансового портфеля, состоящего из собственных и приобретенных ценных бумаг;

· рыночный, связанный с вероятным колебанием как рыночных процентных ставок собственной национальной денежной единицы, так и курса зарубежных валют.

Риск подразделяется на динамический и статический. Динамиче­ский риск связан с возникновением непредвиденных изменений стоимости основного капитала вследствие принятия управленческих решений, а также рыночных или политических обстоятельств. Такие изменения могут привести как к потерям, так и к дополнительным доходам. Статический риск обусловлен возможностью потерь ре­альных активов вследствие нанесения ущерба собственности и по­терь дохода из-за недееспособности организации.

Все участники проекта заинтересованы в том, чтобы не допус­тить возможность полного провала проекта или хотя бы избежать убытка. В условиях нестабильной, быстро меняющейся ситуации необходимо учитывать все возможные последствия от действий конкурентов, а также изменения конъюнктуры рынка. Поэтому ос­новное назначение анализа риска состоит в том, чтобы обеспечить партнеров информацией, необходимой для принятия решений о це­лесообразности участия в некотором проекте, и предусмотреть меры по защите от возможных финансовых потерь.

При анализе риска могут использоваться следующие условия или предположения:

• потери от риска не зависят друг от друга;

• потери по одному из некоторого перечня рисков не обязатель­но увеличивают вероятность потерь по другим;

• максимально возможный ущерб не должен превышать финан­совых возможностей участников проекта.

Все факторы, влияющие на рост степени риска в проекте, можно условно разделить на объективные и субъективные. Объективные факторы непосредственно не зависят от самой фирмы: это инфляция, конкуренция, политические и экономические кризисы, экология, на­логи и т.д. Субъективные факторы непосредственно характеризуют данную фирму: это производственный потенциал, техническое осна­щение, уровень производительности труда, проводимая финансовая, техническая и производственная политика, в частности выбор типа контракта между инвестором и заказчиком. Последний фактор играет особо важную роль для фирмы, поскольку от типа контракта зависят степень риска и величина вознаграждения по окончании проекта.

Исследование риска целесообразно проводить в следующей по­следовательности:

• выявление объективных и субъективных факторов, влияющих на конкретный вид риска;

• анализ выявленных факторов;

• оценка конкретного вида риска с финансовых позиций, опре­деляющая либо финансовую состоятельность проекта, либо его эко­номическую целесообразность;

• установка допустимого уровня риска;

• анализ отдельных операций по выбранному уровню риска;

• разработка мероприятий по снижению риска.

Финансирование проекта, являясь одним из наиболее важных условий обеспечения эффективности его выполнения, должно быть нацелено на обеспечение потока инвестиций для планомерного вы­полнения проекта, на снижение капитальных затрат и риска проекта за счет оптимальной структуры инвестиций и получения налоговых преимуществ. В плане финансирования проекта должны учитывать­ся следующие виды рисков:

• нежизнеспособности проекта;

• налоговый;

• неуплаты задолженностей;

• незавершения строительства.

Высокая степень риска проекта приводит к необходимости по­иска путей искусственного снижения его (риска) возможных по­следствий на состояние дел фирмы.

В существующей практике применяются главным образом четы­ре основных способа управления риском: распределение риска меж­ду всеми участниками проекта (передача части риска соисполните­лям), страхование, резервирование средств на покрытие непредви­денных расходов и диверсификация.

Анализ рисков подразделяется на два взаимно дополняющих друг друга вида: качественный, главная задача которого состоит в определении факторов риска и обстоятельств, приводящих к риско­вым ситуациям, и количественный, позволяющий вычислить разме­ры отдельных рисков и риска проекта в целом.

Меры риска

Наиболее распространена точка зрения, согласно которой мерой риска коммерческого (финансового) решения или операции следует считать среднеквадратичное отклонение (положительный квадрат­ный корень из дисперсии) значения показателя эффективности этого решения или операции. Действительно, поскольку риск обусловлен недетерминированностью исхода решения (операции), то, чем меньше разброс (дисперсия) результата решения, тем более он пред­сказуем, т.е. меньше риск. Если вариация (дисперсия) результата равна нулю, риск полностью отсутствует. Например, в условиях ста­бильной экономики операции с государственными ценными бума­гами считаются безрисковыми.

Чаще всего показателем эффективности финансового решения (операции) служит прибыль.

Рассмотрим в качестве иллюстрации выбор некоторым лицом одного из двух вариантов инвестиций в условиях риска. Пусть име­ются два проекта Л и В, в которые указанное лицо может вложить средства. Проект А в определенный момент в будущем обеспечивает случайную величину прибыли. Предположим, что ее среднее ожи­даемое значение, математическое ожидание, равно т_А с дисперсией S_A. Для проекта В эти числовые характеристики прибыли как случайной величины предполагаются равными соответственно т_в и S_B~. Среднеквадратичные отклонения равны соответственно S_A и S_B.

Возможны следующие случаи:

a) т_А = т_в, S_A < S_B, следует выбрать проект Л;

b) т_А > т_в, S_A < sb, следует выбрать проект А;

c) т_А > т_в, S_A = sb, следует выбрать проект Л;

d) т_А > т_в, S_A > S_B;

e) т_А < т_в, S_A < S_B.

В последних двух случаях решение о выборе проекта А или В зависит от отношения к риску ЛПР. В частности, в случае d) проект А обеспечивает более высокую среднюю прибыль, однако он и бо­лее рискован. Выбор при этом определяется тем, какой дополни­тельной величиной средней прибыли компенсируется для ЛПР за­данное увеличение риска. В случае е) для проекта А риск меньший, но и ожидаемая прибыль меньше.

Магистральные модели экономики. Магистральная модель накопления основных производственных фондов в конце планового периода. Модель фон Неймана расширяющейся экономики.

Классическая (исходная) модель Неймана строится при следующих предпосылках:

1. экономика, характеризуемая линейной технологией, состоит из отраслей, каждая из которых обладает конечным числом производственных процессов, т.е. выпускается несколько видов товаров, причем допускается совместная деятельность отраслей;

2. производственные процессы разворачиваются во времени, причем осуществление затрат и выпуск готовой продукции разделены временным лагом;

3. для производства в данный период можно тратить только те продукты, которые были произведены в предыдущем периоде времени, первичные факторы не участвуют;

4. спрос населения на товары и, соответственно, конечное потребление в явном виде не выделяются;

5. цены товаров изменяются во времени.

Перейдем к описанию модели Неймана. На дискретном временном интервале с точками рассматривается производство, в котором n видов затрат с помощью m технологических процессов превращаются в n видов продукции. Мы не будем указывать число отраслей, так как в дальнейшем не понадобится подчеркивать принадлежность товаров или технологий к конкретным отраслям. В модели Леонтьева технологические коэффициенты были отнесены к единице продукта. В модели Неймана, принимая в качестве производственных единиц не отрасли, а технологические процессы, удобно отнести эти коэффициенты к интенсивности производственных процессов.

Интенсивностью производственного процесса j называется объем продуктов, выпускаемых этим процессом за единицу времени. Уровень интенсивности j -го процесса в момент времени t обозначим через (). Заметим, что является вектором, число компонент которого соответствует числу выпускаемых j -ым процессом видов товаров и .

Предположим, что функционирование j -го процесса () с единичной интенсивностью требует затрат продуктов в количестве

и дает выпуск товаров в количестве

Введем обозначения . Пара характеризует технологический потенциал, заложенный в j -ом процессе (его функционирование с единичной интенсивностью). Поэтому пару можно назвать базисом j -го производственного процесса, имея в виду, что для любой интенсивности соответствующую пару затраты-выпуск можно выразить как . Поэтому последовательность пар

представляющих собой затраты и выпуски всех производственных процессов в условиях их функционирования с единичными интенсивностями, будем называть базисными процессами.

Все m базисных процессов описываются двумя матрицами

где A - матрица затрат, B - матрица выпуска. Вектор называется вектором интенсивностей. Соответствующие этому вектору затраты и выпуски по всем m процессам можно получить как линейную комбинацию базисных процессов (6.4.1) с коэффициентами :

Говорят, что в производственном процессе базисные процессы (6.4.1) участвуют с интенсивностями . Как видно из (6.4.2), неймановская технология, описываемая двумя матрицами A и B единичных уровней затрат и выпуска, является линейной (см. предпосылку 1) в начале параграфа). Рассматривая все допустимые "смеси" базисных процессов, получаем расширенное множество производственных процессов

которое и отражает допустимость совместной деятельности отраслей. Возможность совместного производства нескольких продуктов в одном процессе следует из того, что в каждом процессе j может быть отличной от нуля более чем одна из величин . Множество (6.4.3) представляет собой неймановскую технологию в статике (в момент t). Если в матрице A положить n=m, матрицу B отождествить с единичной матрицей, а интерпретировать как вектор валового выпуска, то (6.4.2) превращается в леонтьевскую технологию.

Продолжим описание модели Неймана. Согласно предпосылок 2) и 3), затраты в момент t не могут превышать выпуска , соответствующего предыдущему моменту t-1 (рис. 6.3).

Поэтому должны выполняться условия:

где 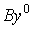- вектор запаса товаров к началу планируемого периода.

Обозначим через , вектор цен товаров. Неравенство (6.4.4) можно трактовать как непревышение спроса над предложением в момент t. Поэтому в стоимостном выражении (в ценах момента t) должно быть:

По предположению 5) прибыль базисного процесса на отрезке [t-1,T] равна величине 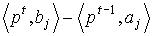, т.е. затраты осуществляются по цене начала периода, а готовая продукция - по цене момента ее реализации. Таким образом, издержки по всем базисным процессам можно записать как , а выручку - как (рис. 6.4).

Будем говорить, что базисные процессы неубыточны, если , неприбыльны - если

В модели Неймана предполагается неприбыльность базисных процессов. Это объясняется тем, что издержки и выручки разведены во времени, т.е. относятся к разным моментам времени, и в условиях расширяющейся экономики "характерен случай падения цен (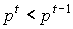)", т.е. покупательская способность денег в момент t будет выше, чем в момент t-1. С таким обоснованием можно согласиться или не согласиться. Главная же причина неприбыльности базисных процессов заложена в определении экономического равновесия. Поясним это чуть подробнее.

Основной предмет исследования Дж. фон Неймана - это возможность существования равновесия в рассматриваемой им динамической модели экономики при заданных в каждый момент ценах. Как следует из определения 5.2, при равновесии в условиях совершенной конкуренции имеет место стоимостной баланс (см. (5.3.8)). Таким образом, в условиях равновесия не создается никакой прибыли, и неравенство http://www.csu.ac.ru/%7Erusear/ME_Ruda/Chapter6/par6_4.html - %286.4.6.%29(6.4.6) является отражением этого факта. Поэтому, если в (6.4.6) для некоторого базисного процесса j имеет место строгое неравенство, т.е. предложение превышает спрос:

то должно быть . Иначе говоря, отсутствие "отрицательной прибыли" обеспечивается нулевой интенсивностью. Отсюда получаем

Описание модели Неймана завершено. Совокупность неравенств и уравнений (6.4.4) -(6.4.7):

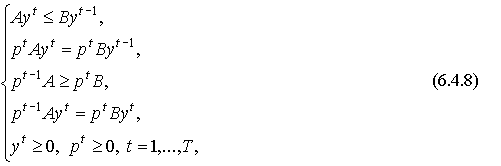
где 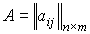и - матрицы затрат и выпуска соответственно, называется (динамической) моделью Неймана.

Определение 6.2. Говорят, что в экономике наблюдается сбалансированный рост производства, если существует такое постоянное число 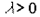, что для всех m производственных процессов

Постоянное число называется темпом сбалансированного роста производства.

Содержательно (6.4.9) означает, что все уровни интенсивности возрастают одинаковыми темпами

Раскрывая рекуррентно правую часть (6.4.9), получаем

где 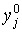- интенсивность процесса j, установившаяся к началу планового периода. Заметим, что t в правой части (6.4.10) является показателем степени, а в левой - индексом.

В случае сбалансированного роста производства, с учетом постоянства темпа роста, последовательность называется стационарной траекторией производства.

Определение 6.3. Говорят, что в экономике наблюдается сбалансированное снижение цен, если существует такое постоянное число 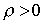, что для всех n товаров

Постоянное число называется нормой процента.

Содержательно (6.4.11) означает, что цены на все товары снижаются одинаковыми темпами

Название "норма процента" для темпа снижения принято по ассоциации с показателем нормы процента (нормы доходности) в формуле сложного процента , где R0 - сумма начального вложения, Rn - получаемая через n периодов конечная сумма, 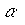- норма процента. Так как в определении 6.3 речь идет о снижении, то "норма процента" в (6.4.11) входит с отрицательным знаком ().

Из равенства (6.4.10) получаем

где - цены, установившиеся к началу планового периода.

В случае сбалансированного снижения цен последовательность называется стационарной траекторией цен.

Подставляя (6.4.10) и (6.4.12) в модель Неймана (6.4.8), получаем ее "стационарную" форму:

Эта система соотношений показывает, что по стационарным траекториям y и p экономика развивается согласно неизменному динамическому закону. Поэтому такую ситуацию естественно назвать равновесной.

http://www.csu.ac.ru/%7Erusear/ME_Ruda/Chapter6/def6.4. Определение 6.4. Четверка 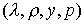, где y - стационарная траектория производства, p - стационарная траектория цен, а и - соответствующие им темп сбалансированного роста производства и норма процента (темп сбалансированного снижения

123	Поделиться:

Воспользуйтесь поиском по сайту: