 |
В12. Задачи на теорию вероятности
|
|
|
|
Задания В3
В12. Задачи на теорию вероятности
Задания В3 |
1. 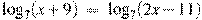
|
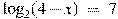 .
.
3 
| |
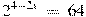 .
.
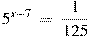 .
.
 .
.
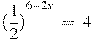 .
.
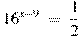 .
.
 .
.
 .
.
11. 
| |
 .
.
Задания В4 Задание1 | ||||
В равнобедренном треугольнике ABC с основанием AC боковая сторона AB равна 8, а  . Найдите высоту, проведенную к основанию
. . Найдите высоту, проведенную к основанию
.
| ||||
Задача 2 | ||||
В равнобедренном треугольнике ABC с основанием AC боковая сторона AB равна 25, а высота, проведенная к основанию, равна 20. Найдите косинус угла 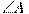 . .
|
Задача 3 | ||||||
В треугольнике ABC угол C равен 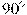 , ,  , ,  . Найдите . Найдите 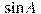 . .
| ||||||
Задача 4 | ||||||
В треугольнике ABC угол C равен 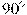 , , 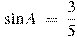 , , 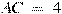 . Найдите AB. . Найдите AB.
| ||||||
Задача 5 | ||||||
В треугольнике ABC угол C равен 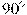 , , 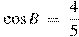 , ,  . Найдите AC. . Найдите AC.
| ||||||
Задача 6 | ||||||
В треугольнике ABC угол C равен 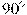 , ,  , ,  . Найдите tgA. . Найдите tgA.
| ||||||
Задача 7 | ||||||
В треугольнике ABC угол C равен 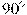 , ,  , , 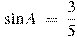 . Найдите BC. . Найдите BC.
| ||||||
Задача 8 | ||||||
В треугольнике ABC угол C равен 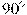 , , 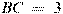 , ,  . Найдите . Найдите 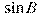 . .
| ||||||
Задача 9 | ||||||
В треугольнике ABC угол C равен 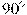 , ,  , , 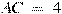 . Найдите tgA. . Найдите tgA.
| ||||||
Задача 10 | ||||||
В треугольнике ABC  , ,  , ,  . Найдите высоту CH. . Найдите высоту CH.
| ||||||
Задача 11 | ||||||
В треугольнике ABC угол C равен 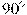 , ,  , , 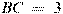 . Найдите . Найдите 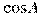 . .
| ||||||
Задача 13 | ||||||
В треугольнике ABC угол C равен 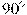 , , 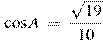 , ,  . Найдите AB. . Найдите AB.
| ||||||
Задача 14 | ||||||
В треугольнике ABC угол C равен 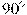 , ,  , ,  . Найдите . Найдите 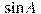 . .
| ||||||
Задача 15 | ||||||
В треугольнике ABC угол C равен 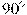 , ,  , ,  . Найдите tgA. . Найдите tgA.
| ||||||
Задача16
| ||||||
В треугольнике ABC  , ,  , ,  . Найдите высоту CH. . Найдите высоту CH.
| ||||||
| ||||||
| ||||||
Задача 17
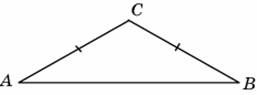
В треугольнике  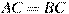 , угол , угол  равен равен 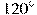 , , 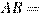 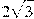 . Найдите . Найдите 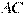 . .
| ||||||
Задача 18 | ||||
В треугольнике  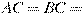  , угол , угол  равен равен 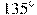 . Найдите высоту . Найдите высоту  . .
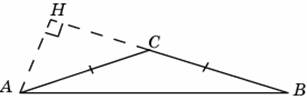
| ||||
Задача 19 | ||||
В треугольнике  угол угол  равен равен 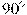 , ,  , , 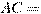 4. 4. 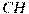 — высота. Найдите — высота. Найдите  . .

| ||||
Задача 20 | ||||
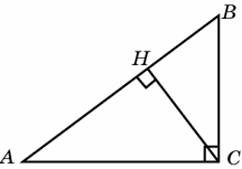
В треугольнике  угол угол  равен равен 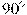 , , 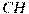 — высота, — высота, 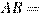 5, sin 5, sin  0,6. Найдите 0,6. Найдите 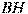 . .
| ||||
| ||||
Задача 21
В треугольнике  угол угол  равен равен 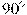 , , 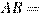 5, 5, 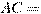 4. Найдите синус внешнего угла при вершине 4. Найдите синус внешнего угла при вершине  . .

| ||||
Задача 22 | ||||
В параллелограмме 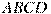 высота, опущенная на сторону высота, опущенная на сторону  , равна 3, , равна 3, 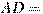 4. Найдите синус угла 4. Найдите синус угла  . .

| ||||
Задача 23 | ||||
Основания равнобедренной трапеции равны 6 и 12. Боковые стороны равны 5. Найдите синус острого угла трапеции.

| ||||
| ||||
Задача 24
В параллелограмме  высота, опущенная на сторону высота, опущенная на сторону  , равна 3, , равна 3, 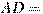 4. Найдите синус угла 4. Найдите синус угла  . .

| ||||
Задача 25 | ||||
Основания равнобедренной трапеции равны 6 и 12. Боковые стороны равны 5. Найдите синус острого угла трапеции.

| ||||
Задача 26 | ||||
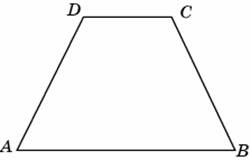
Большее основание равнобедренной трапеции равно 12. Боковая сторона равна 5. Синус острого угла равен 0,8. Найдите меньшее основание.

| ||||
| ||||
Меньшее основание равнобедренной трапеции равно 6. Высота трапеции равна 10. Тангенс острого угла равен 2. Найдите большее основание.
|
Задания В5 Задание1 | ||||||||||||||||||||
Для транспортировки 45 тонн груза на 1300 км. можно использовать одного из трех перевозчиков. Причем у каждого из них своя грузоподъемность используемых автомобилей. Сколько рублей придется заплатить за самую дешевую перевозку за один рейс?
| ||||||||||||||||||||
Задача 2 | ||||||||||||||||||||
Интернет-провайдер (компания, оказывающая услуги по подключению к сети Интернет) предлагает три тарифных плана.
Пользователь планирует, что его трафик составит 600 Mb и, исходя из этого, выбирает наиболее дешевый тарифный план. Сколько рублей заплатит пользователь за месяц, если его трафик действительно будет равен 600 Mb? | ||||||||||||||||||||
Задача 3 | ||||||||||||||||||||
Для изготовления книжных полок требуется заказать 48 одинаковых стекол в одной из трех фирм. Площадь каждого стекла 0,25 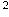 . В таблице приведены цены на стекло, а также на резку стекол и шлифовку края. Сколько рублей нужно заплатить за самый выгодный заказ? . В таблице приведены цены на стекло, а также на резку стекол и шлифовку края. Сколько рублей нужно заплатить за самый выгодный заказ?
| ||||||||||||||||||||
| ||||||||||||||||||||
Задача 4
Клиент хочет арендовать автомобиль на сутки для поездки протяженностью 700 км. В таблице приведены характеристики трех автомобилей и стоимость их аренды. Помимо аренды клиент обязан оплатить топливо для автомобиля на всю поездку. Какую сумму в рублях заплатит клиент за аренду и топливо, если выберет самый дешевый вариант?
Цена дизельного топлива 19 р. За литр, бензина 22 р. За литр, газа 14 р. За литр. | ||||||||||||||||||||
Задача 5 | ||||||||||||||||||||
Телефонная компания предоставляет на выбор три тарифных плана.
Абонент выбрал наиболее дешевый тарифный план, исходя из предположения, что общая длительность телефонного разговора составляет 700 минут в месяц. Какую сумму он должен заплатить за месяц, если общая длительность разговоров в этом месяце действительно будет равна 700 мин? Ответ дайте в рублях.
| ||||||||||||||||||||
| Задача 6 Семья из трех человек едет из Санкт-Петербурга в Вологду. Можно ехать поездом, а можно — на своей машине. Билет на поезд стоит 770 рублей на одного человека. Автомобиль расходует 11 литров бензина на 100 километров пути, расстояние по шоссе равно 700 км, а цена бензина равна 19,5 руб. за литр. Сколько рублей придется заплатить за наиболее дешевую поездку на троих? | ||||||||||||||||||||
| ||||||||||||||||||||
| ||||||||||||||||||||
| ||||||||||||||||||||
Строительной фирме нужно приобрести 40 кубометров строительного бруса. У неё есть 3 поставщика. Сколько рублей придется заплатить за самую дешевую покупку с доставкой? Цены и условия доставки приведены в таблице.
| ||||||||||||||||||||
Задача 10 | ||||||||||||||||||||
| Для строительства гаража можно использовать один из двух типов фундамента: бетонный или фундамент из пеноблоков. Для фундамента из пеноблоков необходимо 2 кубометра пеноблоков и 3 мешка цемента. Для бетонного фундамента необходимо 2 тонны щебня и 20 мешков цемента. Кубометр пеноблоков стоит 2250 рублей, щебень стоит 600 рублей за тонну, а мешок цемента стоит 200 рублей. Сколько рублей придется заплатить за материал, если выбрать самый дешевый вариант? | ||||||||||||||||||||
| ||||||||||||||||||||
| Задача 11 | ||||||||||||||||||||
Клиент хочет арендовать автомобиль на сутки для поездки протяженностью 600 км. В таблице приведены характеристики трех автомобилей и стоимость их аренды. Помимо аренды клиент обязан оплатить топливо для автомобиля на всю поездку. Какую сумму заплатит клиент за аренду и топливо, если выберет самый дешевый вариант?
Цена дизельного топлива 18,5 р. За литр, бензина 20,5 р. За литр, газа 17,5 р. За литр. | ||||||||||||||||||||
Задача 12 | ||||||||||||||||||||
От дома до дачи можно доехать на автобусе, на электричке или на маршрутном такси. В таблице показано время, которое приходится затратить на каждый участок пути. Какое наименьшее время потребуется на дорогу? Ответ дайте в часах
| ||||||||||||||||||||
| ||||||||||||||||||||
Строительная фирма планирует купить 70  пеноблоков у одного из трех поставщиков. Цены и условия доставки приведены в таблице. Сколько рублей нужно заплатить за самую дешевую покупку с доставкой? пеноблоков у одного из трех поставщиков. Цены и условия доставки приведены в таблице. Сколько рублей нужно заплатить за самую дешевую покупку с доставкой?
| ||||||||||||||||||||
| Задача 14 | ||||||||||||||||||||
Из пункта А в пункт D ведут три дороги. Через пункт В едет грузовик со средней скоростью 42 км/ч, через пункт С едет автобус со средней скоростью 43 км/ч. Третья дорога — без промежуточных пунктов, и по ней движется легковой автомобиль со средней скоростью 66 км/ч. На рисунке показана схема дорог и расстояние между пунктами по дорогам. Все три автомобиля одновременно выехали из А. Какой автомобиль добрался до D позже других? В ответе укажите, сколько часов он находился в дороге.

|
|
|
|
Задания В6
| ||||
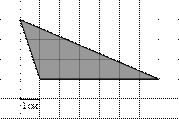
| ||||
| ||||

| ||||
| ||||
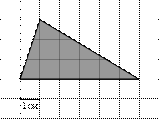
| ||||
| ||||

| ||||
| ||||

| ||||
| ||||

| ||||
| ||||

| ||||
| ||||
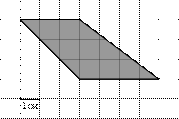
| ||||
| ||||

| ||||
| ||||
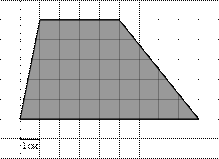
| ||||
| ||||
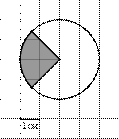
| ||||
| ||||

|
Задания В7
Задача 1 | ||||
Найдите значение выражения  . .
| ||||
Задача 2 | ||||
Найдите значение выражения  . .
| ||||
Задача3 | ||||
Найдите значение выражения  . .
| ||||
Задача 4 | ||||
Найдите значение выражения  . .
| ||||
Задача 5 | ||||
Найдите значение выражения 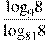 . .
| ||||
Задвча 6 | ||||
Найдите значение выражения 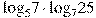 . .
| ||||
Задача 7 | ||||
Найдите значение выражения 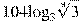
| ||||
Задача 8 | ||||
Найдите значение выражения 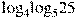
| ||||
Задача 9 | ||||
Найдите значение выражения 
| ||||
Задача 10 | ||||
Найдите значение выражения 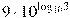 . .
| ||||
Задача 11 | ||||
Найдите значение выражения 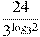 . .
|
Задача 12 | ||||
Найдите значение выражения 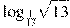 . .
| ||||
Задача 13 | ||||
Найдите значение выражения 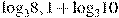 . .
| ||||
Задача14 | ||||
Найдите значение выражения 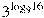 . .
| ||||
Задача 15 | ||||
Найдите значение выражения  . .
| ||||
Задача 16 | ||||
Найдите значение выражения  . .
| ||||
Задача 17 | ||||
Найдите значение выражения  . .
| ||||
Задания В8
Задача 1 | ||||
Прямая  параллельна касательной к графику функции параллельна касательной к графику функции 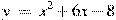 . Найдите абсциссу точки касания. . Найдите абсциссу точки касания.
| ||||
Задача 2 | ||||
Прямая 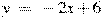 является касательной к графику функции является касательной к графику функции 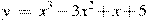 . Найдите абсциссу точки касания. . Найдите абсциссу точки касания.
| ||||
Задача 3 | ||||
На рисунке изображен график функции 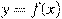 , определенной на интервале , определенной на интервале 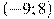 . Определите количество целых точек, в которых производная функции . Определите количество целых точек, в которых производная функции 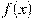 отрицательна. отрицательна.

|
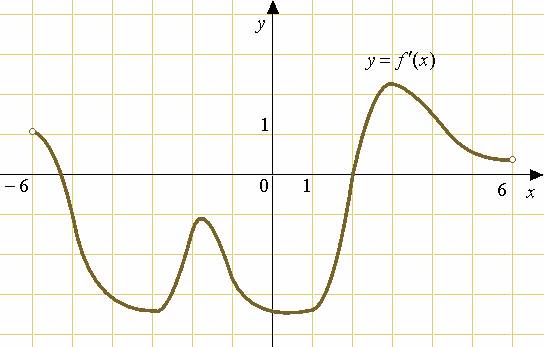
Задача 4
На рисунке изображен график производной функции 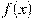 , определенной на интервале , определенной на интервале  . Найдите точку экстремума функции . Найдите точку экстремума функции  на интервале на интервале  . .
|
Задача 5
На рисунке изображен график производной функции 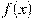 , определенной на интервале , определенной на интервале 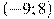 . Найдите промежутки возрастания функции . Найдите промежутки возрастания функции 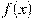 . В ответе укажите сумму целых точек, входящих в эти промежутки. . В ответе укажите сумму целых точек, входящих в эти промежутки.
 Задача 6
На рисунке изображен график функции
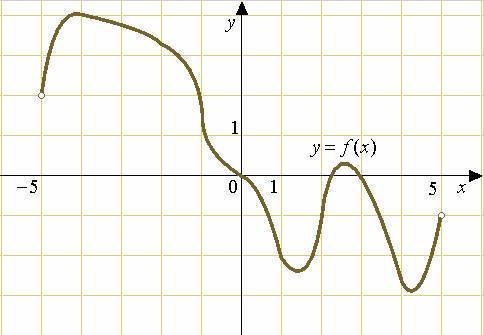
Задача 6
На рисунке изображен график функции 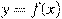 , определенной на интервале , определенной на интервале 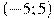 . Определите количество целых точек, в которых производная функции . Определите количество целых точек, в которых производная функции 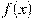 отрицательна. отрицательна.
 Задача 7
На рисунке изображен график производной функции
Задача 7
На рисунке изображен график производной функции 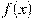 , определенной на интервале , определенной на интервале 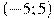 . Найдите количество точек экстремума функции . Найдите количество точек экстремума функции  на отрезке на отрезке  . .
 Задача 8
Задача 8
|
Задания В9
Задача 1 | ||||
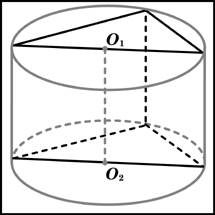
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

|
Задача 2 | ||||
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.

|
Задача 3
Прямоугольный параллелепипед описан около сферы радиуса 1. Найдите его объем.

|
Задача 5
| Задача 4 | |||
|
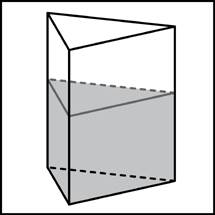
| В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 16 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? |
Задача 6 | ||||
В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны  . Найдите объем цилиндра, описанного около этой призмы. . Найдите объем цилиндра, описанного около этой призмы.
|
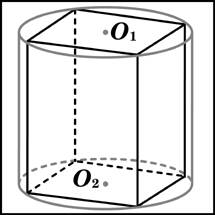
Задача 7 | ||||
В основании прямой призмы лежит квадрат со стороной 7. Боковые ребра равны 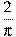 . Найдите объем цилиндра, описанного около этой призмы. . Найдите объем цилиндра, описанного около этой призмы.
|
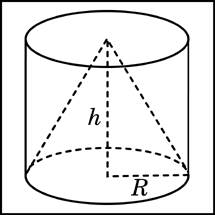
Задача 8
Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 25.
| ||||
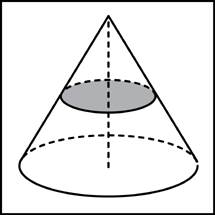
Задача 9
Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
| ||||
| ||||
| ||||
|
| Задания В 10 | ||||
Для одного из предприятий-монополистов зависимость объёма спроса на продукцию q (единиц в месяц) от её цены p (тыс. руб.) задаётся формулой:  . Определите максимальный уровень цены p (в тыс. руб.), при котором значение выручки предприяти . Определите максимальный уровень цены p (в тыс. руб.), при котором значение выручки предприяти
Воспользуйтесь поиском по сайту:  ©2015 - 2026 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...
|