 |
В дБ на длину волны для горных пород
|
|
|
|
Краткая теория
Плотность энергии; интенсивность
Важнейшей особенностью сейсмической волны является энергия, связанная с движением среды при прохождении по ней волны. Обычно рассматривается не полная энергия волны, а энергия, выделяющаяся в окрестности точки наблюдения. Энергия, заключенная в единице объема в окрестности некоторой точки, называется плотностью энергии.
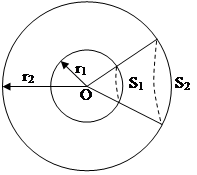
|
| Рис.1 Фронты S1 и S2 сферической волны, расходящейся от центра соответственно радиусов r1 и r2 |
Рассмотрим сферическую гармоническую продольную волну см. рис.1., у которой радиальное смещение при фиксированном значении r расстояния от источника до приемника определяется по формуле
и = А cos (ωt + g),
где t - время, ω - круговая частота, g - фазовый угол. Согласно приведенной формуле амплитуда смещения и изменяется от -А до +А.Поскольку смещение меняется со временем, каждый элемент среды имеет скорость смещения u = du/dt и связанную с ней кинетическую энергию dEk. В каждом элементе объема dV с плотностью r, она равна
dEk, = (r dV) u²/2.
Плотность кинетической энергии составит
E = dEk/ dV = ru²/2 = rω²А²sin²(ωt + g)/2.
Это выражение изменяется от нуля до максимума, равного rω²А²/2.
С волной связана также потенциальная энергия, обусловленная упругими деформациями, которые возникают при ее прохождении. По мере колебания среды энергия переходит из кинетической в потенциальную и обратно, полная же энергия остается неизменной. Когда смещение частицы равно нулю, потенциальная энергия равна нулю, а кинетическая — максимальна, а при максимальном смещении частицы от исходного положения вся энергия является потенциальной. Поскольку полная энергия равна максимальному значению кинетической энергии, плотность энергии Е для гармонической волны равна
|
|
|
Е = rω²А²/2 = 2p² rf²А².
Таким образом, плотность энергии пропорциональна первой степени плотности среды и квадратам частоты и амплитуды волны.
Интересующей нас величиной является также плотность потока энергии, то количество энергии, протекающей в единицу времени через единичную площадку, нормальную к направлению распространения волны. Рассмотрим цилиндр бесконечно малого поперечного сечения dS, ось которого параллельна направлению распространения волны, а длина равна расстоянию, пройденному ею за время dt. Полная энергия, заключенная внутри цилиндра высотой udt в момент времени t, составляет EudtdS. В момент t + dt вся эта энергия покинет цилиндр, пройдя через один из его торцов. Поделив ее на площадь основания цилиндра dS и на интервал времени dt, получим плотность потока энергии (или интенсивность) - количество энергии, проходящей через единичную площадь за единицу времени:
I = Eu.
Для гармонической волны имеем
I = ruω²А²/2= 2p² ruf²А².
На рис.1 показан фронт сферической волны, расходящейся от центра. Рассмотрим два участка волновых фронтов S1 и S2 радиусов r1 и r2 соответственно. Энергия, протекающая наружу через сферический «колпачок» S1 за одну секунду, должна быть равна энергии, протекающей наружу за одну секунду через сферический «колпачок» S2 (так как энергия перемещается только в радиальном направлении). Поток энергии за секунду равен произведению интенсивности на площадь, поэтому
I1 S1= I2 S2.
Поскольку площади S1 и S2 пропорциональны квадратам их радиусов, получаем
I1/I2 = Е2/Е1 = S1/S2 = (r1/r2)2.
Таким образом, геометрическое (сферическое) расхождение энергии приводит к тому, что интенсивность и плотность энергии сферических волн уменьшаются обратно пропорционально квадрату расстояния от источника. У плоской волны лучи не расходятся. Рис. 1 можно также рассматривать как поперечное сечение цилиндрической волны, возбужденной очень длинным линейным источником. Дуги dS1 и dS2 представляют собой цилиндрические волновые фронты. Поскольку длина дуг пропорциональна радиусу, цилиндрическое расхождение приводит к изменению интенсивности обратно пропорционально радиусу:
|
|
|
I1/I2 = Е2/Е1 = (r1/r2),
Или в общем виде
I1/I2 = Е2/Е1 = (r1/r2)m
где т = 0,1 или 2 соответствуют плоской, цилиндрической или сферической волнам.
Отношения интенсивностей, энергий или мощностей, как правило, выражают в децибелах (дБ). Значение в децибелах представляет собой 10·lg от отношения интенсивностей, энергий или мощностей. Поскольку интенсивности изменяются как квадрат амплитуды, значение в децибелах задается также как 20·lg от отношения амплитуд.
Поглощение
Рассмотрим еще два механизма, заставляющие уменьшаться плотность энергии волны. В реальной действительности по мере прохождения волн через среду упругая энергия, связанная с волновым движением распределяется не только в зависимости от геометрии распространения волны, но постепенно поглощается этой средой, переходя, в конце концов, в тепло. Этот процесс называется поглощением. За счет него волновое движение в итоге полностью исчезает.
Поглощение меняется с частотой, поэтому измерить его очень трудно. Результаты лабораторных измерений, производимых всегда на высоких частотах, нельзя переносить на реальные полевые условия. При полевых измерениях нужно учитывать эффекты отражения и преломления, и то, что путь волн проходит в неоднородной среде. Трудности измерений приводят к сильным различиям измеренных значений показателей степени поглощения.
Экспериментально установлено, что при распространении упругих волн в горных породах их амплитуда вследствие поглощения уменьшается с расстоянием по закону близкому к экспоненциальному. Следовательно, зависимость для уменьшения амплитуды из-за одного только поглощения можно записать в следующем виде
А=А0·e- ax,
где А и А0 — значения амплитуды волны в двух точках среды (см. рис.2), находящихся на расстоянии х друг от друга в направлении распространения волны, а α - коэффициент поглощения.
|
|
|

|
| Рис.2. Расположение точек среды с амплитудами А0 и А. Направление распространения волны - ОХ |
Другим показателем поглощения является коэффициент затухания h, который характеризует уменьшение амплитуды с течением времени:
А = А0е -ht cos ωt,
где t – задержка по времени между двумя точками волнового фронта.
Кроме того, для оценки поглощающих свойств среды удобно пользоваться логарифмическим декрементом затухания d, который определяется по формуле:

Его можно выразить через коэффициент затухания как
d = hT = h/f = 2πh/ω ()
где Т – период. d измеряется в неперах. Непер - это натуральный логарифм отношения амплитуд, время регистрации которых отличается на один период. Аналогично d измеряется в децибелах на длину волны. Эта величина определяется как 20 логарифмов отношения амплитуд, зафиксированных в точках, расстояние от источника для которых отличается на одну длину волны.
Экспериментальные данные позволяют предположить, что коэффициент поглощения a приблизительно пропорционален частоте, то есть для конкретной породы произведение al (или hT) — примерно постоянная величина. Измерения декремента поглощения продольных волн для горных пород в общем распадаются на диапазоны, показанные в табл. 1. Значения для S-волн, в среднем, составляют 1/2—1/3 от значений для Р-волн.
Таблица 1
Логарифмический декремент поглощения продольных волн a
в дБ на длину волны для горных пород
| Магматические породы | 0,04 - 0,02 |
| Осадочные породы | 0,16 - 0,02 |
| Газоносные породы | 0,63 - 0,06 |
Механизмы, посредством которых энергия упругих волн преобразуется в тепло, еще полностью не раскрыты. Вероятно, наиболее важными механизмами являются внутреннее трение в форме трения скольжения (или прилипания, а затем скольжения) и вязкие потери в поровых флюидах. Последний механизм, наиболее значителен в сильно проницаемых породах. Другими эффектами, имеющими меньшую значимость, служат потеря части тепла, образующегося в фазе сжатия волнового движения, путем теплопроводности, пьезоэлектрические и термоэлектрические эффекты и энергия, идущая на образование новых поверхностей (играющая заметную роль только вблизи источника). Многие из постулированных механизмов предсказывают, что поглощениезависит от частоты (в жидкостях пропорционально частоте).
|
|
|
Для теоретической подготовки к занятиям дайте ответы на вопросы:
1. Что такое сейсмическая волна?
2. Какие волны называются объемными? Укажите разновидности объемных волн.
3. Какие волны называются сферическими? - плоскими?
4. Какая среда в сейсмической разведке называется: а) идеально-упругой; б) поглощающей.
|
|
|


