 |
Примеры формализаций экстремальных задач
|
|
|
|
Методы оптимизации
Формализация экстремальных задач
Все задачи на максимум и минимум будем называть экстремальными задачами или задачами оптимизации.
Экстремальные задачи, возникающие в естественных науках или на практике, обычно ставятся словесно, без формул, в содержательных терминах той области, где эта задача возникла. Чтобы можно было воспользоваться теорией, необходим перевод задач на математический язык. Этот перевод называется формализацией. Одна и та же задача может быть формализована разными способами, и простота решения зачастую сильно зависит от того, насколько удачно она формализована.
Этап формализации
Точно поставленная экстремальная задача включает в себя три основных элемента: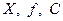 
:
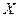‑ множество допустимых элементов (область определения функционала 
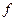); функционал 
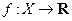‑ отображение множества 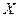на действительную ось;
ограничение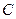 
‑ подмножество 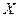, т. е. 
.
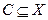Существует стандартная запись правильно формализованной задачи:
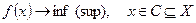(з)
Точки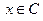 
называются допустимыми по ограничению. Если 
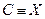, то задача (з) называется задачей без ограничений.
Задачу на максимум всегда можно свести к задаче на минимум:
.
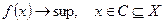
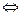
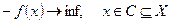Далее мы, как правило, будем для определенности исследовать задачи минимизации. Если необходимо исследовать задачу на максимум и на минимум, то будем писать:
.
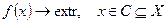Определение 1. Допустимая по ограничению точка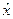 
называется точкой абсолютного минимума в задаче (з), если 
(аналогично, допустимая по ограничению точка 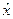называется точкой абсолютного максимума в задаче (з), если 
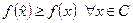). При этом будем писать 
(
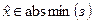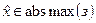). Иногда будем писать, для краткости, 
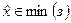, подразумевая, что это 
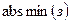и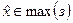 
, подразумевая, что это 
.
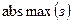Иногда точку абсолютного минимума (максимума) задачи называют решением задачи.
|
|
|
Кроме глобальных (абсолютных) экстремумов будем также рассматривать локальные экстремумы. Дадим их строгое определение. Пусть в задаче (з) 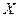‑ нормированное пространство.
Определение 2. Допустимая по ограничению точка 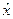называется точкой локального минимума в задаче (з), если 
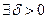такое, что для любых 
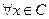, удовлетворяющих условию 
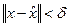, выполняется неравенство 
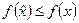. При этом будем писать 
.
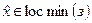Иными словами, если 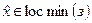, то существует окрестность 
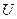точки 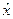, такая, что 
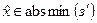, где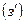 
: 
.
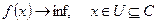Примеры формализаций экстремальных задач
1). Задача Аполлония (III в. до н. э.): найти кратчайшее расстояние от точки до эллипса.
Возьмем систему координат и расположим удобным образом. Требуется найти кратчайшее расстояние от точки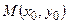 
до эллипса, задаваемого уравнением 
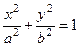. Тогда задача Аполлония допускает следующую формализацию:
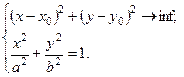
Здесь 
; 
; 
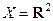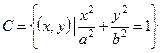. Задача относится к гладким конечномерным задачам с ограничениями типа равенств. Общая задача Аполлония изложена в величайшем творении «Коника» или «Конические сечения» (5-я книга): имеется совокупность конических сечений (гипербола, эллипс, парабола) и точка в коническом сечении. Нужно найти максимальное и минимальное расстояния до линии конического сечения.
2). Задача Кеплера (17 век): в шар вписать цилиндр максимального объема.
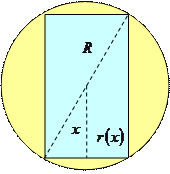Рассмотрим сечение шара плоскостью большого круга. Пусть 
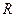– радиус шара, 
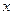– половина высоты.
.
По теореме Пифагора: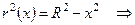 
.
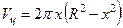Формализация задачи Кеплера:
.
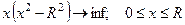Функционал: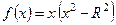 
; множество 
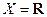; ограничение 
.
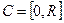3). Транспортная задача. Относится к задачам линейного программирования, которые возникли в 40-50е годы XX века.
Имеется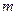 
баз,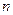 
магазинов и некоторый продукт 
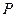. Его надо доставить с баз в магазины по потребности при минимальной стоимости перевозок (т. е. какое количество данного продукта 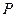надо перевезти из каждой базы в каждый магазин, чтобы суммарная стоимость перевозок была минимальной). Введем обозначения:
|
|
|
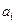– количество продукта, которое есть на 
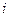-й базе, 
;
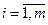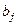– количество продукта, необходимое 
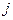-му магазину, 
;
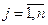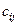– стоимость перевозки единицы продукта с 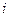-й базы в 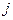-й магазин;
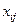– планируемое количество единиц продукта, перевозимое с 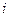-й базы в 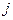-й магазин.
Тогда суммарная стоимость перевозки задается выражением
;
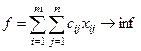а ограничения имеют вид:
а).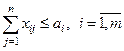 
– нельзя вывезти больше того, что есть на базе,
б).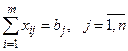 
– столько продуктов магазину необходимо,
в).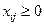 
– очевидное ограничение на величину перевозки.
В данной задаче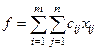 
; ограничения 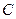– соотношения а), б), в); 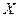– совокупность .
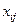Очень часто при исследовании экстремальных задач будем использовать следующие теоремы.
Теорема Вейерштрасса. Непрерывная функция на непустом ограниченном замкнутом подмножестве пространства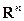 
достигает своих абсолютных максимума и минимума.
Следствие из теоремы Вейерштрасса. Если функция 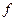непрерывна на 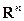и 
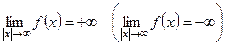, то 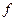достигает своего абсолютного минимума (максимума) на любом замкнутом подмножестве .
|
|
|
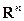